“Теория автоматического управления”

1. Порядок разработки систем автоматического управления.

?- комплексный вопрос: удовлетворяет ли разработанная система требованию заказчика, если удовлетворяет то процедуры синтеза выполнены (конец синтеза).Если не удовлетворяет то идет на этап Перестановки задачи.

1.Постановка задачи. Заказчик и разработчик должны друг-друга понять. Здесь нужно сформулировать задание в терминах и теориях ТАУ, нужно выбрать критерии качества, по которым будет возможно количественно оценить работу сис-мы.(время переходного процесса, перерегулирование и т.д)

2. Моделирование. Включает:

1. Математическое моделирование

-Нормальная форма Коши

- Форма пространства состояний

-Форма передаточных функций (Передаточная функция — отношение изображения выходного сигнала к изображению входной велечены при нулевых начальных условиях.)

2. Компьютерное моделирование

-Непосредственное моделирование(LTJ объекты- компьютерная реализация)

-Иммитационное моделирование(Simuling).

3. Анализ. Подзадачи:

1) Оценки устойчивости системы.

2)Определение частотных характеристик (АЧХ, ФЧХ, ВЧХ, МЧХ, АФЧХ, ЛАЧХ, ЛФЧХ, объединяющая 2 последнии- ЛАФЧХ, АФХ, ЛАФХ).

3)Определение временных характеристик( переходная, весовая).

Переходная функция — это реакция системы на единичный ступенчатый сигнал.

Весовая функция — это реакция системы на единичный импульс.

4) Оценка запасов устойчивости

5)Оценки управляемости и наблюдаемости

4. Синтез.

1) Выбор при помощи методов регулятора для синтезируемой системы:

- частотный метод

-модальный метод

-метод аналитического конструирования регулятора

2) Оценка показателей качества системы.

2. Определение разомкнутой и замкнутых передаточных функций скалярных систем автоматического управления.

3. Оценка устойчивости непрерывных систем автоматического управления по корням характеристического полинома. Управляемость и наблюдаемость векторных систем автоматического управления.

4. Оценка устойчивости непрерывных систем автоматического управления при помощи алгебраических и частотных критериев.

Определение: Устойчивость –это способность динамической системы будучи выведенный из состояния равновесия, каким-либо внешними факторами и явлениями, воздеств-ся в состояние равновесия, после снятия этих внешних факторов или воздействий.

Существует 2 способа определения устойчивости без вычисления корней:

-алгебраические (Критерий Гурвица,Рауса)

-частотные (Критерий Найквиста, Михайлова)

Критерии устойчивости позволяют судить о знаках корней характеристического уравнения, не находя этих корней, а следовательно судить об устойчивости.

Алгебраические критерии:

- коэффициенты характеристического уравнения, которые определяются коэффициентами и постоянными времени системы.

Критерий Гурвица

Он позволяет определить устойчивость как разомкнутой системы, так и замкнутых систем.Удобен при машинном счёте, но он имеет ограничение на порядок систем при ручном счёте.

Это матрица n на n

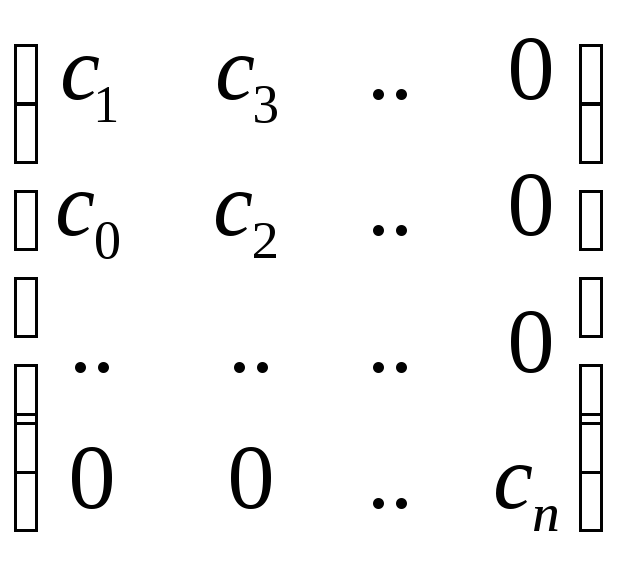
На главной диагонали располагаем индексы в порядке возрастания.

Элементы любого столбца матрицы заполняется сверху вниз в порядке убывания индекса, причем выше проставляются 0-ли.

определители Гурвица

Формулировка критерия:Для устойчивости необходимо и достаточно чтобы при все определители Гурвица были положительны.

Если размер матрицы n=1

Для устойчивости необходимо и достаточно чтобы коэффициенты характеристического уравнения были положительны.

Если размер матрицы n=2

Для устойчивости необходимо и достаточно чтобы коэффициенты характеристического уравнения были положительны.

Если размер матрицы n=3

Для устойчивости необходимо и достаточно чтобы коэффициенты характеристического уравнения были положительны и второй определитель так же был положительным.

Если размер матрицы n=3

Для устойчивости необходимо и достаточно чтобы коэффициенты характеристического уравнения были положительны и третий определитель так же был положительным.

Критерий Рауса

Раус предложил критерий устойчивости САУ в виде алгоритма, по которому заполняется специальная таблица с использованием коэффициентов характеристического уравнения:

1) в первой строке записываются коэффициенты уравнения с четными индексами в порядке их возрастания;

2) во второй строке - с нечетными;

3) остальные элементы таблицы определяется по формуле:

, где ,- номер строки,k - номер столбца.

4) Число строк таблицы Рауса на единицу больше порядка характеристического уравнения

Ri	i\k	1	2	3	4
-	1	c11 = a0	c21 = a2	c31 = a4	...
-	2	c12 = a1	c22 = a3	c32 = a5	...
r3 = c11/c12	3	c13 = c21-r3c22	c23 = c31-r3c32	c33 = c41-r3c42	...
R4 = c12/c13	4	c14 = c22-r3c23	c24 = c32-r4c33	c34 = c42-r4c43	...
...	...	...	...	...	...

Критерий Рауса: для того, чтобы САУ была устойчива, необходимо и достаточно, чтобы коэффициенты первого столбца таблицы Рауса c₁₁, c₁₂, c₁₃... имели одинаковый знак, то есть должны быть больше нуля.

Преимущества:

1)порядок диффура, описывающего систему не ограничен;

2)можно автоматизировать подсчет коэф-ов;

3)при появлении первого нулевого или отрицат-ого коэф-та подсчет можно прекратить

4)позволяет производить подсчет правых, левых, нулевых, чисто мнимых корней;

5)используется для анализа как разомкнутых, так и замкнутых систем.

Частотные критерии.

Критерий Михайлова

Не имеет ограничений на порядок систем. Может использоваться для определения устойчивости замкнутых и незамкнутых систем.

Критерий Михайлова основан на рассмотрении характеристиче­ского уравнения САР, в котором вместо p используется j. В этом слу­чае имеем функцию комплексной переменной вида:

F ( р ) = р=j

F ( j ) = U ( ) + j V( ),

где

U ( ) =;

V( ) =.

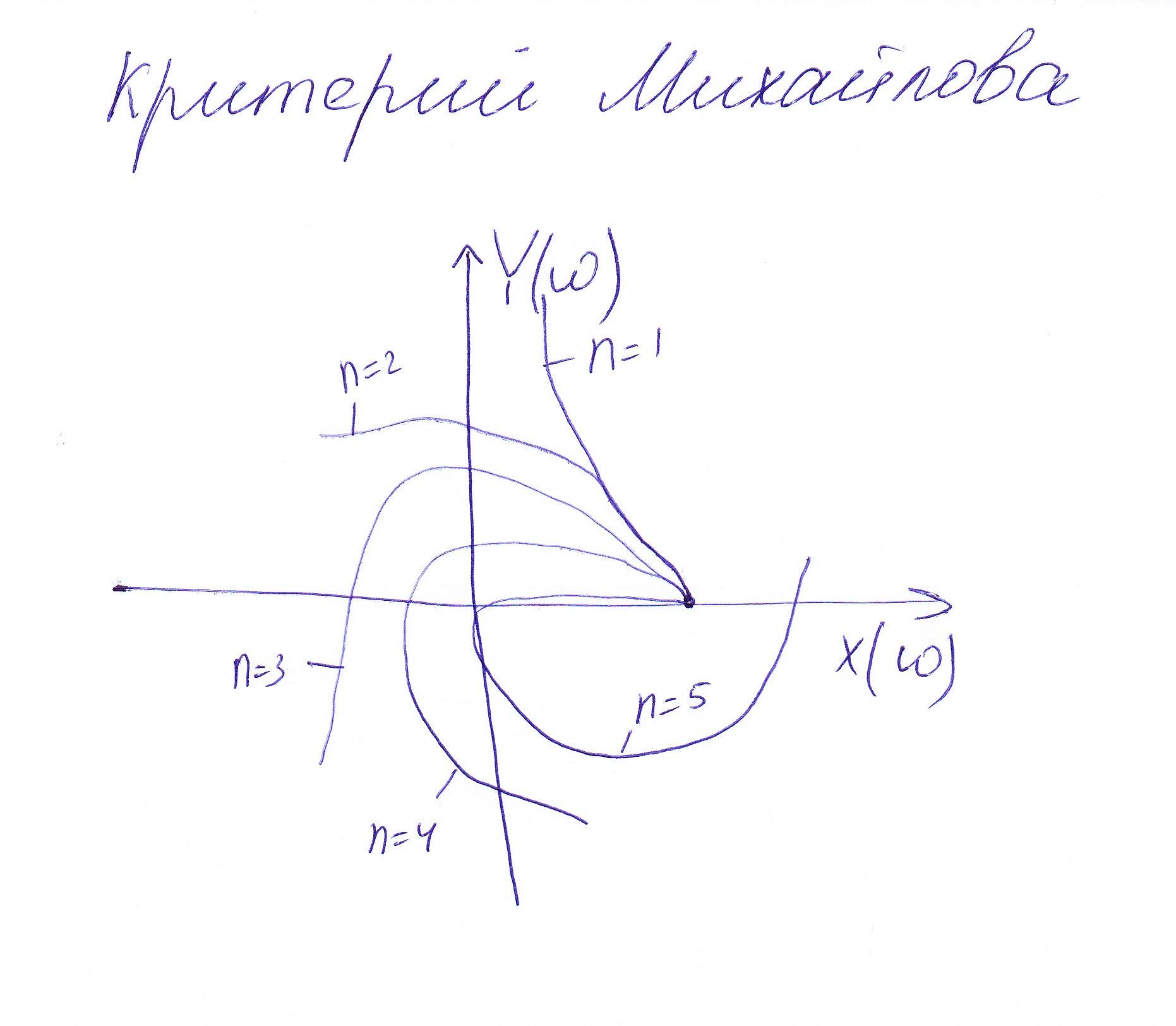
Система устойчива по критерию Михайлова, если при изменении частоты  от 0 до + годограф Михайлова повернётся в положительном направлении (против часовой стрелки), начиная с вещественной положительной полуоси, на число квадрантов, равное порядку характеристического уравнения, то есть на угол n / 2, при этом нигде не обращаясь в нуль. Если годограф Михайлова проходит через начало координат, то САР находится на границе устойчивости. САР неустойчива по критерию Михайлова, если годограф проходит n квадрантов непоследовательно или проходит меньшее число квадрантов.

Критерий михайлова позволяет также определить количество правых корней

,где -угол, в котором поворачивается годогроф,-порядок системы,- количество правых частей(корней).

Критерий Найквиста

Особенность критерия Найквиста состоит в том, что он оценивает устойчивость САР по амплитудно-фазовой частотной характеристике её разомкнутой части, называемой годографом Найквиста.

Если разомкнутая часть САР устойчива или находится на границе устойчивости, то для её устойчивости необходимо и достаточно, чтобы годограф Найквиста при изменении частоты  от 0 до + не охватывал точку с координатами [-1, j 0].

При этом возможны 3 случая: (1 – САР устойчива; 2 – САР на границе устойчивости; 3 – САР неустойчива)

1)Разомкнутая система устойчива

Для устойчивости замкнутой системы необходимо и достаточно, чтобы годограф Найквиста при изменении частоты  от 0 до + не охватывал точку с координатами [-1, j 0].

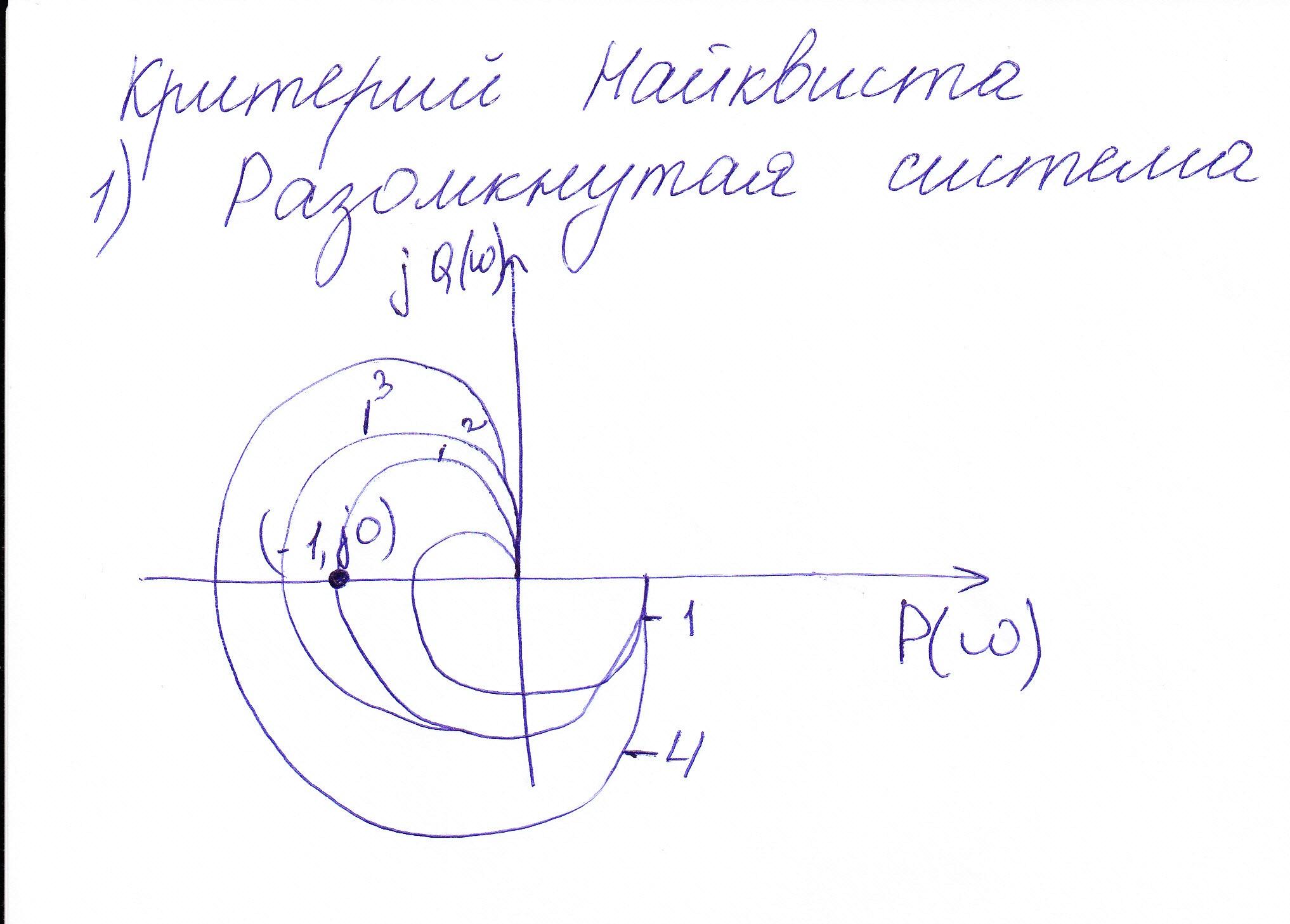
1график- устойчивая замкнутая система

2график- замкнутая система находится на границе устойсивости

3график- замкнутая система неустойчивая

4график –замкнутая система является устойчивой, так как незначительное изменение параметров могут превратить её в неустойчивую.

2) Разомкнутая система на границе устойчивости

Тогда её АФЧХ имеет разрывы, если она на границе аппериодической устойчивости, то получен разрыв при w=0.

В этом случае для применения критерия Найквиста годогрофы АФЧХ разомкнутых систем достраивают другими бесконечного радиуса по часовой стрелке воздвигаясь от w=0 до w=бесконечности начинается всегда с положительной вещественной оси.

Для устойчивости замкнутой системы необходимо и достаточно, чтобы годограф Найквиста при изменении частоты  от 0 до + не охватывал точку с координатами [-1, j 0].

3) Разомкнутая система неустойчива

У таких систем АФЧХ часто имеет инверсную форму.

Если разомкнутая часть САР неустойчива, то для её устойчивости необходимо и достаточно, чтобы при изменении частоты  от 0 до + годограф Найквиста охватывал точку [-1, j0] l / 2 раз в положительном направлении (против часовой стрелки), где l – число корней характеристического уравнения с положительной вещественной частью. Переход АФЧХ разомкнутой части системы при увеличении  отрезок вещественной оси от -1 до - сверху-вниз считается положительным, а снизу вверх – отрицательным. Если АФЧХ начинается на данном отрезке, при =0 или заканчивается при =, то считается что АФЧХ совершает пол перехода. Замкнутая часть системы устойчива, если разность между числом положительных и отрицательных переходов годографа Найквиста, через отрезок вещественной оси от -1 до - равна l / 2 раз (l – число корней характеристического уравнения)

5. Определение запасов устойчивости замкнутых систем автоматического управления.

Для того чтобы систему можно было использовать, недостаточно сделать ее устойчивой, нужно снабдить ее некоторым запасом устойчивости.

УСТОЙЧИВАЯ СИСТЕМА В НЕКОТОРЫХ СЛУЧАЯХ МОЖЕТ БЫТЬ НЕУСТОЙЧИВОЙ:

1. При математическом описание систем применяются различные допущения, отбрасываются какие–то малосущественные факторы. Поэтому модель описывает процессы протекающие в системе в какой-то погрешностью. В результате по модели система устойчивая, а на практике может оказаться неустойчивой.

2. Все элементы системы изготавливаются в пределах заданных технологических допусков( не существует 2-ух идентичных экземпляров одной и той же системы).При этом 1 экземпляр- устойчивый, а другой нет.

3. Многие параметры системы подвергаются старению, т.е меняются с течением времени. Обычно это элементы накапливающие энергию. Система ранее устойчивая может стать неустойчивой.

4. На работу системы оказывает влияние условие окружающей среды ( температура, давление). В результате одна система в одних условиях устойчива, а в других условиях нет!

ЗАПАС УСТОЙЧИВОСТИ (ЗУ)- это мера удаленности системы от границы устойчивости. Количественно ЗУ определяется по 2-ум показателям:

-ЗУ по амплитуде ∆А, ∆L (∆L=20 lg∆А)

-ЗУ по фазе ∆ф

Запас устойчивости по амплитуде – это минимальный отрезок действительной оси P(w) , характеризующий расстояние между критической точкой (-1, j0) и ближайшей точкой пересечения годографом Найквиста вещественной оси.

Запас устойчивости по фазе – это минимальный угол, образуемый радиусом, проходящим через точку пересечения годографа Найквиста с окружностью единичного радиуса с центром в начале координат и вещественной отрицательной полуосью.

Эти показатели определяют на основание критерия Нейквиста по АФЧХ и ЛАФЧХ разомкнутой системы, но являются они запасом устойчивости замкнутой системы.

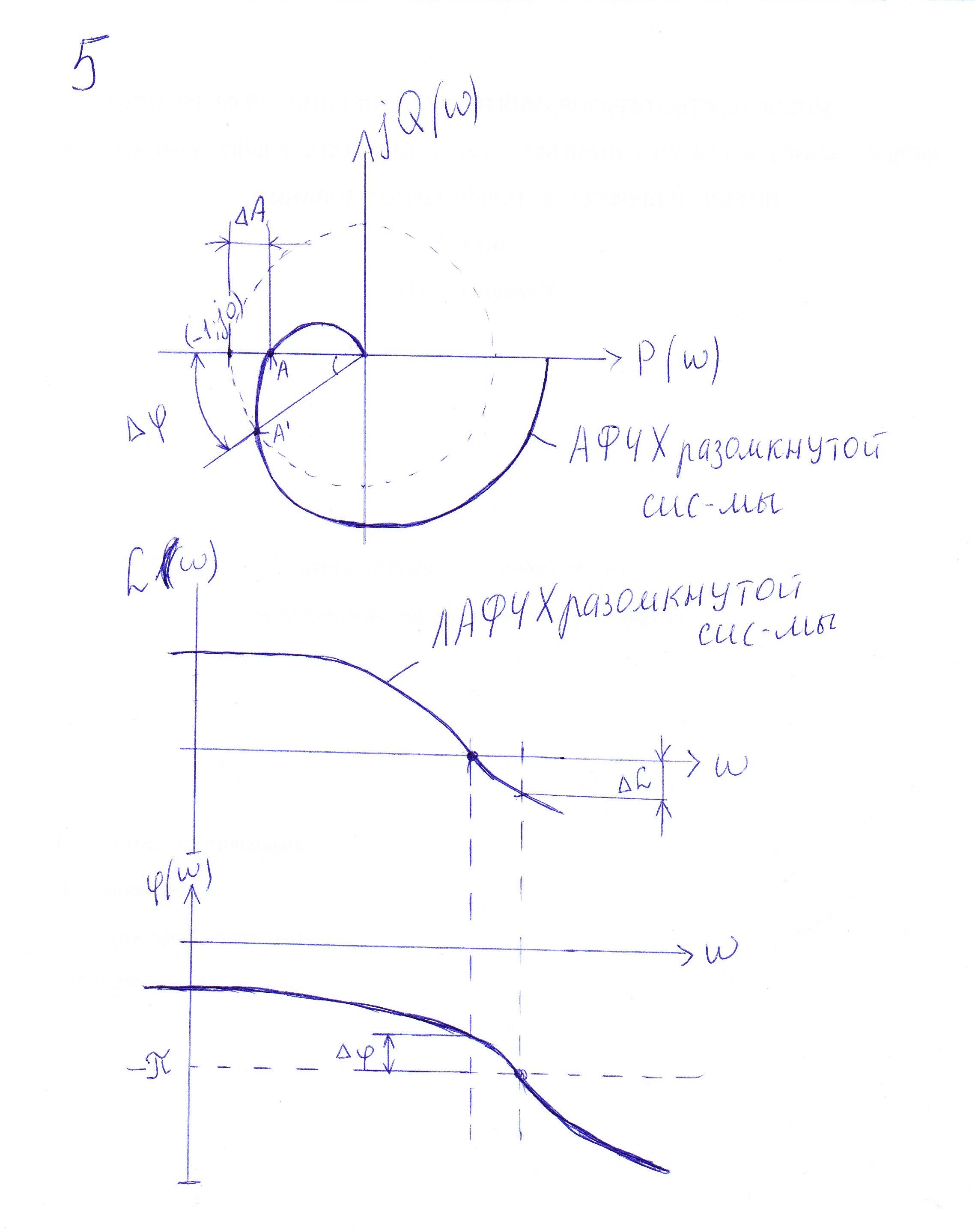
Если ситема обладает слишком большим запасом устойчивости то она становиться инерционной(т.е. длительной)

∆А= 0,1…0,5

∆ф= 30…60 градусов

∆А и ∆ф исключают друг-друга, достаточно рассмотреть одно их двух.

6. Оценка устойчивости дискретных систем автоматического управления по корням характеристического полинома, а также при помощи алгебраических и частотных критериев.

7. Оценка показателей качества процесса управления. Статическая и динамическая точность. Показатели качества переходного процесса. Интегральные показатели качества.