2.3. Применение метода ветвей и границ

к решению задач линейного целочисленного программирования

Рассмотрим задачу ЦЛП в матричной форме записи. Обозначим ОДП этой задачи D, а ОДП ЗЛП без ограничений целочисленности - G. Точно так же обозначим соответствующие системы ограничений, а сами задачи будем называть D-задача и G-задача.

max CX

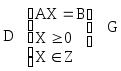
D представляет собой часть G. G будем рассматривать в качестве исходного множества (рис.2).

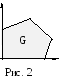
Решим вначале G-задачу. Пусть при решении этой задачи получен оптимальный план Х_G. Значение целевой функции на нем z_G - оптимум G-задачи - будем использовать в качестве границы . В самом деле,

z_G СХХG

z_G СХХD

Если план Х_G целочисленный, то решение задачи окончено. Таким образом, мы ответили на первый и третий вопросы, конкретизирующие метод ветвей и границ.

Предположим, что хотя бы одна компонента Х_G нецелочисленна: х_GiZ.

Целой частью числа называют наибольшее целое число, меньшее или равное данному.

Обозначим целую часть числа х_Gi [х_Gi].

Конкретизируем второй вопрос.

Разобьем D на D₁ и D₂ следующим образом:

D₁={XD: х_i[х_Gi]}

D₂={XD: х_i[х_Gi] + 1}

(т.е. к одному множеству отнесли все допустимые планы, у которых i-я компонента не больше целой части х_Gi, а к другому - у которых не меньше следующего целого числа)

Разбивая D, мы одновременно разбиваем и G (рис.3).

Это разбиение обладает следующими свойствами:

G₁ G₂ G (объединение этих множеств содержится в G, но не равно ему)

D₁ D₂ = D (в устраненном «коридоре» нет ни одной точки с целочисленными координатами)

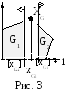
При этом устраняется и план Х_G.

Далее решение задачи продолжается для каждого из подмножеств G₁ и G₂.

Сходимость алгоритма основана на том, что в ограниченной ОДП множество дискретных точек конечно.

Следует отметить, что метод ветвей и границ легко обобщается и на частично целочисленные задачи (в качестве переменной, по которой разбивается множество, выбирают одну из тех, на которые наложены ограничения целочисленности).

2.4. Пример решения задачи целочисленного линейного программирования методом ветвей и границ

Например,

max 2х₁ + х₂

5х₁ + 2х₂10

3х₁ + 8х₂13

х_1,20

х_1,2 Z

Вначале решим эту задачу графически без ограничений целочисленности (рис.4).

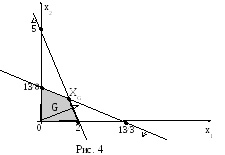
Координаты точки оптимума можно найти, решив систему уравнений:

5х₁ + 2х₂ = 10 х₁=27/17

3х₁ + 8х₂ = 13 х₂=35/34

Х_G = (27/17;35/34), z_G=143/34

Начнем строить дерево, первая вершина которого будет соответствовать всей ОДП нецелочисленной задачи (G), а ее оценка будет равна z_G (рис.5).

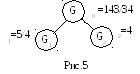
Полученный план не является целочисленным, поэтому возьмем его произвольную нецелочисленную компоненту, например, первую (х₁Z; [х₁] = [27/17] = 1 ) и разобьем ОДП на две части следующим образом:

G₁={XG: х₁1}

G₂={XG: х₁2}

Изобразим это графически (рис.6).

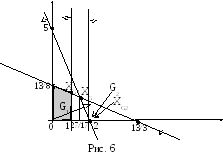
Из рис.7 видно, что G₂ представляет собой одну точку Х_G2=(2;0), следовательно, на этом множестве оптимум задачи равен 4 (₂=4).

План Х_G2 является целочисленным, следовательно, решение целочисленной задачи уже, возможно, найдено. Однако, следует еще найти оценку множества G₁. Она может оказаться не менее 4 (но обязательно не более 143/34). Если это так, то нужно проверить, не является ли целочисленным решение задачи на G₁. Если оно целое, то является решением задачи, а если нет, то процесс решения необходимо продолжить, разбивая G₁.

На G₁ точку оптимума можно найти, решив систему уравнений:

х₁ = 1 х₁=1

3х₁ + 8х₂ = 13 х₂=5/4

Х_G1 = (1; 5/4), z_G=13/4

Оценка меньше 4, следовательно, решением задачи является Х^*=Х_G2=(2;0), z^*=4.