42

Глава 3. Метод ветвей и границ решения задач целочисленного линейного программирования 36

3.1. Постановка задачи целочисленного линейного программирования 36

3.2. Элементы теории графов 37

3.3. Метод ветвей и границ. Общая схема 38

3.4. Применение метода ветвей и границ к решению задач линейного целочисленного программирования 39

Вопросы и упражнения 41

Глава 3. Метод ветвей и границ решения задач целочисленного линейного программирования

3.1. Постановка задачи целочисленного линейного программирования

Задача линейного программирования, переменные которой могут принимать только целые значения, является задачей целочисленного линейного программирования:

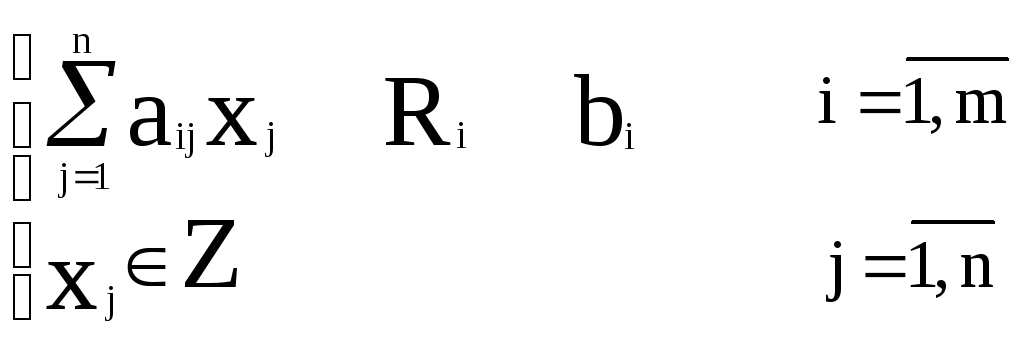
где ; x_j - переменные, a_ij, b_i, c_j - константы.

Записанная в таком виде задача представляет собой полностью целочисленную задачу. Существуют, кроме того, частично целочисленные задачи, в которых ограничения целочисленности наложены только на часть переменных, а остальные переменные могут быть как целыми, так и дробными.

Примером целочисленной задачи в экономике может служить задача производственного планирования, в которой в качестве продукции выступают корабли, дома, вагоны и т.п. предметы, выпуск которых нельзя измерить в непрерывной шкале. Часто переменные в экономико-математических моделях измеряются в количестве человек, которое также не может быть дробным.

На первый взгляд, тривиальным подходом к решению такой задачи является решение задачи линейного программирования без ограничений целочисленности и последующее округление полученного решения до целых. Однако в общем случае такой подход неверен, так как он может привести к одной из двух ошибок. Во-первых, при округлении возможен выход за пределы ОДП, т.е. полученное решение не будет удовлетворять ограничениям. Во-вторых, даже оставшись в пределах ОДП, можно в результате получить неоптимальное решение.

Поэтому округление допустимо использовать лишь в тех случаях, когда по своему экономическому смыслу целочисленные переменные не представляют особо ценные объекты, либо в модели рассматривается очень большое количество таких объектов; т.е. нет необходимости получить точное решение. В противном случае задача должна ставиться, как целочисленная, и к ее решению необходимо применить специфические методы, которые обычно относятся к одной из трех групп:

1. Метод ветвей и границ.

2. Методы отсечения.

3. Методы динамического программирования.

Здесь будет рассмотрен метод из первой группы. Однако, предварительно сформулируем ряд определений.

3.2. Элементы теории графов

Граф представляет собой совокупность двух множеств: множества вершин (углов) и множества ребер (дуг).

Вершина, которая является крайней точкой ребра, называется инцидентной ребру (а ребро соответственно инцидентно вершине). Две вершины с одним инцидентным ребром или два ребра с общей инцидентной вершиной называются смежными. Петля - ребро графа, инцидентное единственной вершине.

Маршрут (путь) - конечная последовательность вершин, каждые две соседние вершины в которой являются смежными. Маршрут простой, если все входящие в него вершины различны.

Цикл - маршрут, первая и последняя вершины которого совпадают. Простой цикл - цикл, в котором единственными совпадающими вершинами являются первая и последняя.

Гамильтонов цикл - простой цикл, содержащий все вершины графа.

Граф, не имеющий простых циклов с более чем двумя различными вершинами, называют ациклическим. Граф является связным, если любые две его вершины можно соединить маршрутом. Связный ациклический граф называется деревом.

Например, граф на рис.17 состоит из вершин{A, B, C, D, E, F} и ребер {a, b, c, d, e, f}. Вершине А, например, инцидентны ребра а, b и с; ребру с инцидентны вершины А и С; вершины А и В являются смежными (так как обе инцидентны ребру b); ребра c и d также смежные (так как оба инцидентны вершине С). Ребро а представляет собой петлю, так как инцидентно только вершине А. Маршруты АВС и АВСD являются простыми, а маршруты АВСВ и АВСА – нет, так как в первом из них вершина В повторяется дважды, а во втором – вершина А. Но маршрут АВСА представляет собой простой цикл, так как первой и последней вершиной в нем является А, и никакие другие вершины в нем не повторяются. Маршрут АВСВА - также цикл, но он не является простым циклом (дважды повторяется вершина В). Так как в графе присутствует маршрут АВСА, граф не является ациклическим. Граф не является и связным, так как нельзя соединить маршрутом, например, вершины А и Е. Гамильтонов цикл в этом графе построить нельзя.

Если рассматривать в качестве отдельного графа, например, граф, состоящий из вершин {B, C, D} и ребер {d, e}, то такой граф будет связным и ациклическим, т.е. его можно назвать деревом. В графе, состоящем из вершин {A, B, C} и ребер {а, b, c, d}, маршрут АВСА будет представлять собой гамильтонов цикл, так как он простой и содержит все три вершины этого графа.