3.3. Метод ветвей и границ. Общая схема

Метод ветвей и границ представляет собой комбинаторный метод, т.е. упорядоченный перебор вариантов и рассмотрение лишь тех из них, которые по некоторым признакам оказываются перспективными. Он имеет достаточно широкую сферу применения, поэтому рассмотрим его общую схему.

Пусть существует некоторая функция f(X), экстремум которой (например, максимум) необходимо найти при некоторой системе ограничений.

Этой системой определяется ОДП задачи - обозначим ее G. Пусть некоторым способом мы можем определить верхнюю границу функции на этой области ₀, т.е. ₀ f(X), XG.

Затем проверяют, не существует ли какой-нибудь очевидный способ нахождения точки X⁰, для которой f(X⁰)=₀. Если он есть, то искомый максимум найден.

Если такого способа нет, то множество G разбивают на подмножества G₁ и G₂ и для каждого из них находят верхнюю границу ₁ и ₂ (при этом ₀₁ и ₀₂). Далее оптимальный план ищут в наиболее перспективном множестве, т.е. в том, которому соответствует наибольшая оценка.

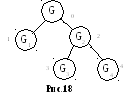
Этот процесс может быть изображен в виде дерева (рис.18). На каждом шаге процесса делается попытка найти точку Х в соответствующем подмножестве, на которой реализуется его верхняя граница. Если попытка не удается, то ветвление продолжают, рассматривая каждый раз наиболее перспективное подмножество (для его выбора сравнивают оценки вершин дерева, из которых нет выходов).

Если попытка найти Х: f(X) =_k удалась, то это будет оптимальный план для всего исходного множества G (поскольку для остальных подмножеств верхние границы заведомо меньше).

При решении задачи на минимум схема та же, но рассматриваются вершины с наименьшей оценкой.

Этот метод всегда сходится, если мы имеем дело с ограниченной дискретной областью.

Чтобы конкретизировать метод ветвей и границ, необходимо установить:

1. алгоритм поиска границ ;

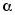2. алгоритм разбиения множества на части;

3. алгоритм поиска Х, реализующего границу ;

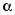4. сходимость метода.

3.4. Применение метода ветвей и границ к решению задач линейного целочисленного программирования

Рассмотрим задачу ЦЛП в матричной форме записи. Обозначим ОДП этой задачи D, а ОДП ЗЛП без ограничений целочисленности - G. Точно так же обозначим соответствующие системы ограничений, а сами задачи будем называть D-задача и G-задача.

max CX

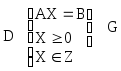
D представляет собой часть G. G будем рассматривать в качестве исходного множества (рис.19).

Решим вначале G-задачу. Пусть при решении этой задачи получен оптимальный план Х_G. Значение целевой функции на нем z_G - оптимум G-задачи - будем использовать в качестве границы . В самом деле,

z_G СХХG;

z_G СХХD.

Если план Х_G целочисленный, то решение задачи окончено. Таким образом, мы ответили на первый и третий вопросы, конкретизирующие метод ветвей и границ.

Предположим, что хотя бы одна компонента Х_G не целочисленна: х_GiZ.

Целой частью числа называют наибольшее целое число, меньшее или равное данному.

Обозначим целую часть числа х_Gi [х_Gi].

Конкретизируем второй вопрос.

Разобьем D на D₁ и D₂ следующим образом:

D₁={XD: х_i[х_Gi]};

D₂={XD: х_i[х_Gi] + 1}

(т.е. к одному множеству отнесли все допустимые планы, у которых i-я компонента не больше целой части х_Gi, а к другому - у которых не меньше следующего целого числа).

Разбивая D, мы одновременно разбиваем и G (рис.20).

Это разбиение обладает следующими свойствами:

G₁G₂ G (объединение этих множеств содержится в G, но не равно ему);

D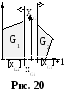₁D₂ = D (в устраненном «коридоре» нет ни одной точки с целочисленными координатами).

При этом устраняется и план Х_G.

Далее решение задачи продолжается для каждого из подмножеств G₁ и G₂.

Сходимость алгоритма основана на том, что в ограниченной ОДП множество дискретных точек конечно.

Следует отметить, что метод ветвей и границ легко обобщается и на частично целочисленные задачи (в качестве переменной, по которой разбивается множество, выбирают одну из тех, на которые наложены ограничения целочисленности).

3.5. Пример решения задачи целочисленного линейного программирования методом ветвей и границ

Требуется решить следующую задачу:

max 2х₁ + х₂

5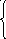х₁ + 2х₂10

3х₁ + 8х₂13

х_1,20

х_1,2 Z

В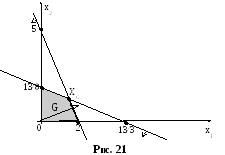начале решим эту задачу графически без ограничений целочисленности. Решение может быть найдено как симплекс-методом, так и графически. Найдем его графически (рис.21).

Координаты точки оптимума можно найти, решив систему уравнений:

5х₁ + 2х₂ = 10 х₁=27/17

3х₁ + 8х₂ = 13 х₂=35/34

Х_G = (27/17;35/34), z_G=143/34.

Начнем строить дерево, первая вершина которого будет соответствовать всей ОДП нецелочисленной задачи (G), а ее оценка будет равна z_G (рис.22).

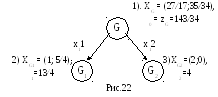
Полученный план не является целочисленным, поэтому возьмем его произвольную нецелочисленную компоненту, например, первую (х₁Z; [х₁] = [27/17] = 1) и разобьем ОДП на две части следующим образом:

G₁ = {XG: х₁1};

G₂ = {XG: х₁2}.

Изобразим это графически (рис.23).

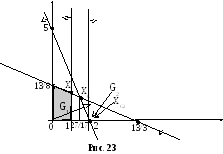
Из рис.6 видно, что G₂ представляет собой одну точку Х_G2=(2;0), следовательно, на этом множестве оптимум задачи равен 4 (₂=4).

План Х_G2 является целочисленным, следовательно, решение целочисленной задачи уже, возможно, найдено. Однако, следует еще найти оценку множества G₁. Она может оказаться не менее 4 (но обязательно не более 143/34). Если это так, то нужно проверить, не является ли целочисленным решение задачи на G₁. Если оно целое, то является решением задачи, а если нет, то процесс решения необходимо продолжить, разбивая G₁.

НаG₁ точку оптимума можно найти, решив систему уравнений:

х₁ = 1 х₁=1

3х₁ + 8х₂ = 13 х₂=5/4

Х_G1 = (1; 5/4), z_G1=13/4.

Оценка меньше 4, следовательно, решением задачи является Х^*=Х_G2=(2;0), z^*=4.

Для задачи с булевыми переменными алгоритм метода ветвей и границ будет тот же, но разбиение проводится по первой по счету переменной, значение которой не равно 0 или 1. На одном подмножестве эта переменная приравнивается 1 (эта ветвь рассматривается вначале), а на другом - нулю.

Следует отметить, что для таких задач разработан более эффективный алгоритм решения (так называемый аддитивный), также основанный на методе ветвей и границ. В нем обычно требуется меньшее число итераций, а кроме того, и расчеты на каждой итерации являются менее трудоемкими, не требуют применения симплекс-метода.