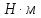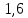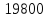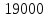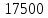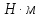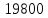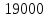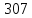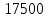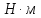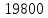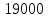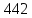- •Ё1. Энерго-кинематический расчёт привода и выбор электродвигателя
- •Определение кпд привода и выбор электродвигателя
- •Определение общего передаточного отношения привода и разбивка его по ступеням
- •Определение частот вращения, крутящих моментов и мощностей на валах
- •Проектирование механических передач
- •Обоснование выбора параметров зубчатых передач
- •Методика расчета 2-х ступенчатого цилиндрического редуктора, выполненного по развернутой схеме
- •2.3. Методика расчета клиноременной передачи
- •Проектный расчет зубчатых передач
- •Проектный расчёт клиноременной передачи
- •Анализ результатов расчёта и выбор оптимального варианта
- •Проектировочный расчёт валов
- •Проверочный расчёт подшипников качения
- •4.1. Расчёт радиальных нагрузок на подшипники качения
- •4.2. Методика расчёта подшипников качения
- •4.3. Результаты расчета подшипников качения
- •5. Выбор и проверочный расчет шпоночных соединений
- •6. Тепловой расчет редуктора
- •7. Выбор системы смазки и смазочных материалов для зубчатых передач и подшипников качения
- •8. Выбор и проверочный расчет муфты
- •9. Проверочный расчет промежуточного вала
Ё1. Энерго-кинематический расчёт привода и выбор электродвигателя
Определение кпд привода и выбор электродвигателя
Кинематическая схема силового привода
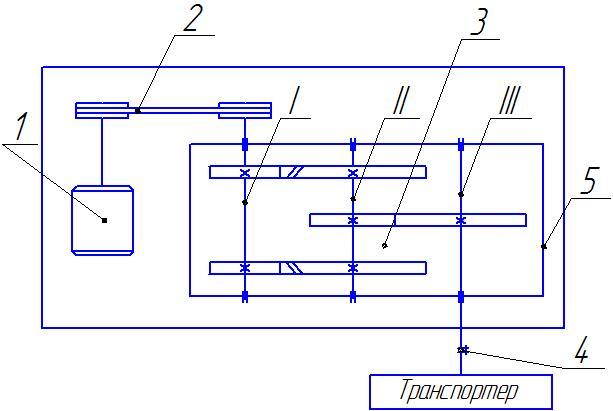
1 – электродвигатель; 2- клиноременная передача; 3 – редуктор; 4 – муфта;5 – рама; I – входной(быстроходный) вал; II – промежуточный вал; III – выходной (тихоходный) вал.
Рис. 1.1
Для привода электродвигателя следует определить его мощность, которая вычисляется по формуле
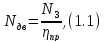
где
 - мощность на выходном валу, Вт;
- мощность на выходном валу, Вт;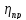 – коэффициент полезного действия (КПД)
привода.
– коэффициент полезного действия (КПД)
привода.
Мощность
на выходном валу определяется по формуле
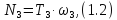
где
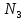 - мощность на выходном валу, Вт;
- мощность на выходном валу, Вт;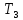 – крутящий момент на выходном валу,
– крутящий момент на выходном валу,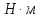 ;
;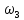 - угловая скорость на валу, рад/с.
- угловая скорость на валу, рад/с.
Угловая скорость на валу вычисляется по формуле
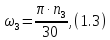
где
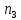 - частота вращения на выходном валу,
об/мин.
- частота вращения на выходном валу,
об/мин.
Численное значение угловой скорости на выходном валу равно
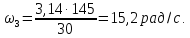
Найдём численное значение мощности на выходном валу
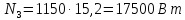
КПД привода может быть вычислен по формуле
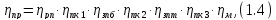
где
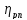 -
КПД ременной передачи;
-
КПД ременной передачи;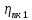 -
КПД подшипников качения валаI;
-
КПД подшипников качения валаI;
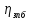 - КПД быстроходной передачи;
- КПД быстроходной передачи;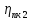 – КПД подшипников качения валаII;
– КПД подшипников качения валаII;
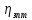 - КПД тихоходной зубчатой передачи;
- КПД тихоходной зубчатой передачи;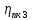 - КПД подшипников качения валаIII,
- КПД подшипников качения валаIII,
 -
КПД муфты.
-
КПД муфты.
Значения
всех коэффициентов, входящих в формулу
(1.4), выбираем по рекомендациям в
соответствии с [1, с.5],
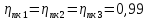 ;
;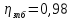 ;
;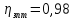 ,
,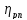 =0,97,
=0,97,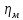 =0,98.
Подставляя эти значения в формулу (1.4),
получаем значение КПД редуктора
=0,98.
Подставляя эти значения в формулу (1.4),
получаем значение КПД редуктора
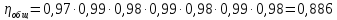
Подставляя
численные значения в (1.1) получим
действительное значение мощности
двигателя
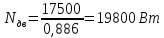
По
[2, с.5] выбираем 3-х фазный двигатель
переменного тока серии 4А с учётом
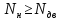 .
.
Тип
двигателя 4А180S2,
асинхронная частота вращения
 об/мин.
об/мин.
Полученные данные запишем в табл. 1.1.
Таблица 1.1.
|
Тип двигателя
|
Номинальная мощность двигателя
|
Синхронная частота вращения
|
Асинхронная Частота
вращения
|
|
4А180S2 |
22,0 |
3000 |
2945 |
Определение общего передаточного отношения привода и разбивка его по ступеням
Передаточное
отношение привода определяется по
формуле
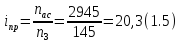 Так как
Так как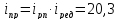 ,
то выбираем передаточные отношения
следующим образом:
,
то выбираем передаточные отношения
следующим образом:
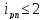 ,
,
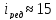 .
В соответствии с [1, с.36] выбираем
.
В соответствии с [1, с.36] выбираем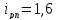 .
.
Определим
передаточное отношение редуктора по
формуле
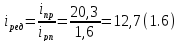
Разбиваем
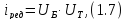
где
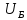 -
передаточное число быстроходной
передачи;
-
передаточное число быстроходной
передачи;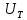 - передаточное число тихоходной передачи.
- передаточное число тихоходной передачи.
В соответствии с рекомендациями выбираем
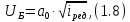
где
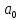 – коэффициент, учитывающий оптимальную
разбивку.
– коэффициент, учитывающий оптимальную
разбивку.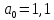 ,
так как схема развернута.
,
так как схема развернута.
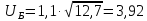
Из формулы (1.7) выразим передаточное число тихоходной передачи
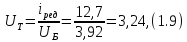
Определение частот вращения, крутящих моментов и мощностей на валах
Мощность вала определяется по формуле
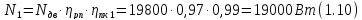
Мощность
на промежуточном валу находим по формуле
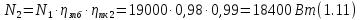
Для
нахождения крутящего момента на входном
валу воспользуемся формулой
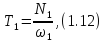
где
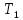 - крутящий момент на входном валу,
- крутящий момент на входном валу,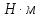 ;
;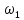 - угловая скорость на входном валу,
рад/с.
- угловая скорость на входном валу,
рад/с.
Угловая
скорость на входном валу вычисляется
по формуле
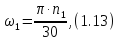
где
 - частота вращения входного вала, об/мин.
- частота вращения входного вала, об/мин.
Частота
вращения входного вала определяется
по формуле
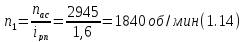
Подставляя
численное значение
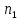 в (1.13), находим угловую скорость на
входном вал 3
в (1.13), находим угловую скорость на
входном вал 3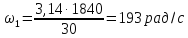
Найдём
крутящий момент на входном валу по
формуле (1.12)
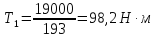
Крутящий
момент на промежуточном валу рассчитывается
по формуле
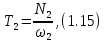
где
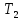 – крутящий момент на промежуточном
валу,
– крутящий момент на промежуточном
валу,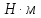 ;
;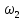 - угловая скорость на промежуточном
валу, рад/с.
- угловая скорость на промежуточном
валу, рад/с.
Угловая
скорость на промежуточном валу вычисляется
по формуле
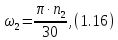
где
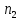 – частота вращения промежуточного
вала, об/мин.
– частота вращения промежуточного
вала, об/мин.
Частота
вращения промежуточного вала определяется
по формуле
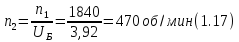
Подставляя
численное значение
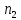 в (1.16), находим угловую скорость на
промежуточном валу
в (1.16), находим угловую скорость на
промежуточном валу
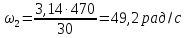
Найдём
крутящий момент на промежуточном валу
по формуле (1.15)
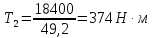
Крутящий
момент электродвигателя рассчитывается
по формуле

где
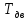 - крутящий момент на валу электродвигателя,
- крутящий момент на валу электродвигателя,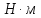 ;
;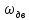 - угловая скорость на валу электродвигателя,
рад/с.
- угловая скорость на валу электродвигателя,
рад/с.
Угловая
скорость на валу электродвигателя
вычисляется по формуле
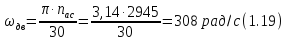
Найдём
крутящий момент на валу электродвигателя
по формуле (1.18)
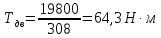
Рассмотрим
случай
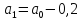
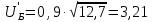
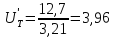
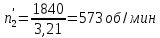
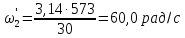
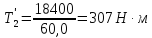
Рассмотрим
случай

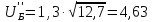
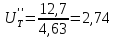
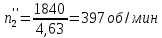
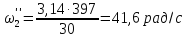
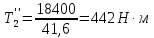
Полученные значения частот вращения, мощностей, крутящих моментов и передаточных чисел приведены в табл. 1.2, 1.3,1.4
Таблица 1.2
Результат
энерго-кинематического расчёта вариант
1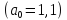
|
Вал |
i(U) |
T,
|
n, об/мин |
N, Вт |
|
Электродвигатель |
|
64,1 |
2945 |
|
|
I |
98,2 |
1840 |
| |
|
3,92 | ||||
|
II |
374 |
470 |
18400 | |
|
3,24 | ||||
|
III |
1150 |
145 |
|
Таблица 1.3
Результат
энерго-кинематического расчёта вариант
2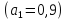
|
Вал |
i(U) |
T,
|
n, об/мин |
N, Вт |
|
Электродвигатель |
1,6 |
64,1 |
2945 |
|
|
I |
98,2 |
1840 |
| |
|
3,21 | ||||
|
II |
|
|
18400 | |
|
3,96 | ||||
|
III |
1150 |
145 |
|
Таблица 1.4
Результат
энерго-кинематического расчёта вариант
3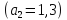
|
Вал |
i(U) |
T,
|
n, об/мин |
N, Вт |
|
Электродвигатель |
1,6 |
64,1 |
2945 |
|
|
I |
98,2 |
1840 |
| |
|
4,63 | ||||
|
II |
|
|
18400 | |
|
2,74 | ||||
|
III |
1150 |
145 |
|

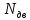 ,
кВт
,
кВт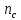 ,
об/мин
,
об/мин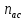 ,
об/мин
,
об/мин