2. Несобственные интегралы

24. Несобственные интегралы второго рода – от неограниченных функций. Главное значение несобственного интеграла второго рода. Несобственные интегралы второго рода

Пусть на полуинтервале задана функция, интегрируемая на любом отрезке, где, однако не интегрируемая на отрезке. В точкеэта функция может быть вовсе не определена и стремиться кпри, любо вовсе не иметь никакого предела при этой базе. Рассмотрим функцию

она определена при . Эта функцияможет иметь предел при(левосторонний предел). Этот предел мы будем называть значением интеграла отпо всему полуинтервалуи обозначать в точности как обычный интеграл:

Итак, дадим такое определение:

        Определение 4.6Пусть функцияудовлетворяет указанным выше условиям на.

Несобственным интегралом второго рода назовём тогда интеграл

значение которого равняется левостороннему пределу

Если этот предел существует, то несобственный интеграл называется сходящимся, а если предела не существует, то расходящимся. Расходящемуся интегралу не приписывается никакого числового значения; в этом случае будем условно писать

    Геометрически вычисление несобственного интеграла второго рода представляет собою (при ) исчерпание площади неограниченной фигуры под графиком функциинадс помощью вычисления площадей ограниченных фигур, получающихся над отрезком, а затем приближением правого концак точке(см. рис.).

Рис.4.7.Итак, площадь неограниченной фигуры, изображённой на рисунке,по определениюравна значению несобственного интеграла.

Пример 4.8Найдём площадьфигуры, расположенной под графиком функциинад промежутком. (Заметим, что функцияне определена прии стремится кпри, так что указанная фигура -- неограниченная и площадь задаётся несобственным интегралом второго рода (см. рис.):

Рис.4.8.

Возьмём и вычислим обычный (собственный) определённый интеграл

Имеем по теореме Ньютона - Лейбница:

Далее вычисляем предел:

Поскольку оказалось, что предел существует, то несобственный интеграл сходится, а искомая площадь равна его значению:

            Замечание 4.4Как и в случае несобственных интегралов первого рода, часто понимают вычисление предела подстановкикак подстановку с верхним предельным значением:

имея в виду, что подстановка верхнего предела интегрирования означает переход к левостороннему пределу при .

При таком обозначении запись вычисления в предыдущем при=мере выглядит так:

Заметим, что здесь мы, глядя на эти вычисления, могли и не заметить, что вычисляемый интеграл -- несобственный. Это произошло потому, что первообразная , которую мы использовали для вычисления подстановки, непрерывна слева в точке.

        Определение 4.7Аналогично интегралу по полуинтервалуот функциис особенностью в точке, определяется несобственный интеграл второго рода от функции, имеющей особенность в точкеполуинтервала:

если существует предел

В случае существования указанного предела интеграл называется сходящимся, а в случае, когда предел не существует, -- расходящимся.     

Замечание 4.5Если сделать замену, то несобственный интеграл от функции, имеющей особенность в правом конце промежутка интегрирования, переходит в несобственный интеграл от функции с особенностью в левом конце промежутка, и наоборот (проверьте это утверждение, сделав заменув интеграле, гдепри). Поэтому свойства несобственных интегралов второго рода достаточно устанавливать лишь в каком-нибудь одном случае, например, в случае особенности в правом конце промежутка, а свойства интегралов с особенностью функции в левом конце будут получаться очевидными переформулировками.

Пример 4.9Рассмотрим интеграл

Если , то подынтегральная функциястремится кпри, так что получается несобственный интеграл второго рода.

Рассмотрим такие случаи:

1) . Тогда интеграл вычисляется так:

поскольку при имееми

2) . Тогда

то есть интеграл расходится, поскольку при.

3) . Тогда

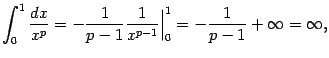
и интеграл снова расходится, поскольку при, если показатель.

Заметим также, что при интеграл не является несобственным: это обычный (то есть собственный) интеграл от непрерывной ограниченной функции. Единственная неприятность получается при, поскольку тогда подынтегральная функцияне определена при(и тождественно равна 1 при). Но мы знаем, согласно одному из свойств определённого интеграла, что значение подынтегральной функции в одной точке можно изменить без изменения значения интеграла. Так что достаточно переопределить значение в 0, положиви получив собственный интеграл

Согласно замечанию 4.5, из примера 4.9 следует, что интеграл

(с особенностью функции в правом конце) сходится при и расходится при.