Временные и частотные характеристики типовых динамических звеньев САУ,их взаимосвязь.

1. Временные характеристики

1. Переходной характеристикой h(t) звена(системы) называется его реакция на единичное ступенчатое воздействие 1(t):

2. Весовой функцией (импульсной характеристикой) w(t) наз. реакция системы на единичную импульсную функцию Дирака δ(t):

;

2. Частотные характеристики

   1. Частотной ПФ системы или ее комплексным коэффициентом передачи называется отношение изображений Фурье выходной и входной переменных:

, где y(t)-выход,g(t)-вход,

;

, ω-частота входного гармонического сигнала

Геометрическая форма ЧПФ

,

;

Частотная ПФ есть комплексное число, модуль которого A(ω) есть отношение амплитуд выходной гармонической переменной к входной, а аргумент φ(ω)-сдвиг фаз между этими переменными.

, где

A(ω) – амплитудная частотная характеристика(АЧХ)

φ(ω) – фазовая частотная характеристика (ФЧХ)

Алгебраическая форма ЧПФ

U(ω) – вещественная частотная характеристика(ВЧХ)

V(ω) – мнимая частотная характеристика(МЧХ)

На комплексной плоскости частотная ПФ W(jω) определяет вектор , длина которого

равна A(ω), а аргумент - угол φ(ω) (аргумент это угол, образованный этим вектором с положительным направлением вещественной оси). Кривую которую вычерчивает конец радиуса вектора при изменении частоты ω от «0» до «∞» называют, амплитудно-фазовой частотной характеристикой(АФЧХ). Аргумент φ(ω) отсчитывается против часовой стрелки.

Логарифмическая амплитудная частотная характеристика (ЛАХ) L(ω):

, где A(ω) – АЧХ

Логарифмической фазовой частотной характеристикой (ЛФХ), называется график зависимости фазовой частотной характеристики φ(ω), изображенной в логарифмических координатах φ(lgω). Единица измерения ЛАХ – децибел, единица измерения логарифмической частоты lgω-декада.

ПРИМЕР:

Некоторые временные и частотные характеристики интегрирующего звена , где T-постоянная времени.

Дифференциальное уравнение:

ПХ:

ЧПФ:

ВЧХ:

МЧХ:

АЧХ:

ФЧХ:

ЛАХ:

Связь временных и частотных характеристик.

ВФ:w(t) и ПХ h(t) связаны:,ПФ W(p) и ЧПФ W(jω): W(jω) получается из ПФ W(p) заменой p→ jω. ПФ W(p) есть преобразование Лапласа от весовой функции w(t)

W(p)=L{w(t)}

Частотная ПФ W(jω) есть преобразование Фурье от весовой

Вычисление ПФ типовых соединений звеньев и стилей; эквивалентные структурные преобразования, правило Мейсона

1. Алгебра ПФ

1. последовательное соединение звеньев

Результирующая ПФ последовательного соединения звеньев равна произведению ПФ звеньев, входящих в соединение.

2. параллельные (согласно-параллельное) соединение

Результирующая ПФ согласно-параллельного соединения звеньев равна сумме ПФ звеньев, входящих в соединение.

3. соединение с обратной связью(встречно-параллельное)

«+» соответствует отрицат. ОС

«-» соответствует положит. ОС

2. Эквивалентные структурные преобразования

Преобразование структурной схемы называется эквивалентным, если результирующая ПФ системы не изменяется.

(таблица преобразований)

3. Правило не касающихся контуров(Теорема Мейсона)

Путь - непрерывная направленная последовательность звеньев, между входной и выходной переменными, в которой ни одна переменная не встречается дважды.

Контур – замкнутый путь (входная и выходная переменные совпадают)

Некасающийся контур(относительно другого контура или пути) – это контур, не имеющий ни одной общей переменной с другими контуром или путем.

Теорема Мейсона. ПФ системы от любого входа g(t) к любому выходу y(t) может быть определена по ф-ле:

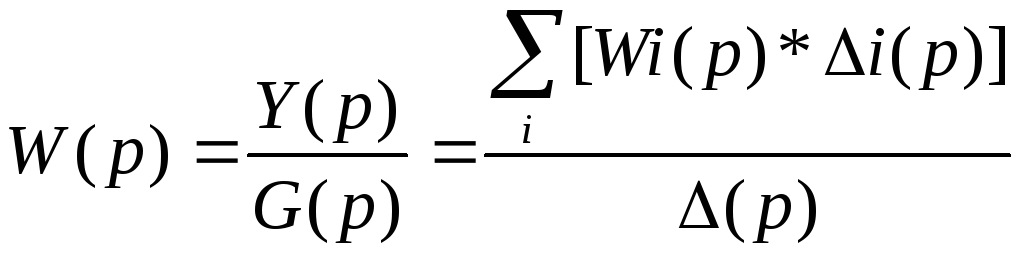, где

, где

- сумма ПФ всех контуров;

- сумма произведений ПФ не касающихся друг друга контуров, взятых попарно;

- сумма произведений ПФ не касающихся друг друга контуров, взятых по три;

- ПФ i-го пути от g(t) до y(t);

,где

- сумма ПФ всех контуров, не касающихся i-го пути;

- сумма произведений ПФ контуров, не касающихся i-го пути и друг друга, взятых попарно;

- сумма произведений ПФ контуров, не касающихся i-го пути и друг друга, взятых потри;