ТАУ3

Устойчивость линейных САУ. Понятие устойчивости.

В простейшем случае понятие устойчивости системы связано со способностью её возвращаться (с определённой точностью) в состояние равновесия после исчезновения внешних сил, которые вывели её из этого состояния.

Наглядно устойчивость равновесий представлена на рисунке:

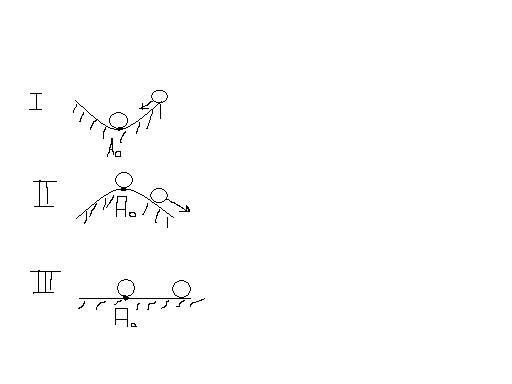
Положение равновесия шара хар-ся точкой . В случае I при при бесконечном отклонении шара от положительного равновесия, он стремится снова возвратиться к положительному равновесию .I – устойчивое положение равновесия; II – неустойчивое; III – безразличное.

Дадим строгое определение устойчивости (дано русским ученым А.М. Ляпуновым в 1892).

Пусть движение САУ описывается дифференциальным ур-ем:

или (1)

где xi – вещественная переменная, характеризующая состояние системы упрощения; xi – известные функции переменных и времени t, удовлетворяющее условиям (существования и единственности) решения ДУ ; - управляющие воздействия, подаваемые на систему .

Если для всех U(t)=0, то система называется свободной.

Определение 1. Состояние свободной системы называется состоянием (положением) равновесия, если для (2)

Очевидно, что если для , то система, находящаяся в состоянии, в нем и останется (скорости нет => не сдвинется в отсутствие внешних сил).

Состояние равновесия называют также невозмущенным движением.

Пусть система под воздействием внешних сил отклонилась от невозмущенного движения, а затем внешние силы при t=t0 сняты. Движение системы с момента времени t0 зависит от начального отклонения , от положения равновесия . Отклонение наз-ся возмущением.

Т.о. - Ур-е возмущенного дв-я

- Ур-е невозмущенного дв-я

Определение 2. (Устойчивость по Ляпунову)

Состоянием равновесия (невозмущенное движение ) наз-ся устойчивым всмысле Ляпунова, если для такое, что для возмущения , удовлетворяющее условию будет выполняться условие для .

Критерии устойчивости делятся на 2 группы:

1. алгебраические критерии (Гурвица, Рауса)

2. частотные критерии (Найквиста, Михайлова)

Критерий устойчивости Гурвица (без д-ва):

Дана линейная стационарная система, характ. полином к-ой имеет вид:

.

Составим по нему матрицу Гурвица размера nxn следующего вида:

Порядок составления:

1. По главной диагонали выписываются по порядку к-ты a1..an

2. строка дополняется таким образом, чтобы слева направо индексы возрастали, и чтобы строки с четными и нечетными индексами чередовались. Вместо к-тов с индексами, меньшими 0 и большими n, пишут нули.

Определителями Гурвица , где i=1,…,n называются главные диагональные миноры м-цы Гурвица.

; ; …

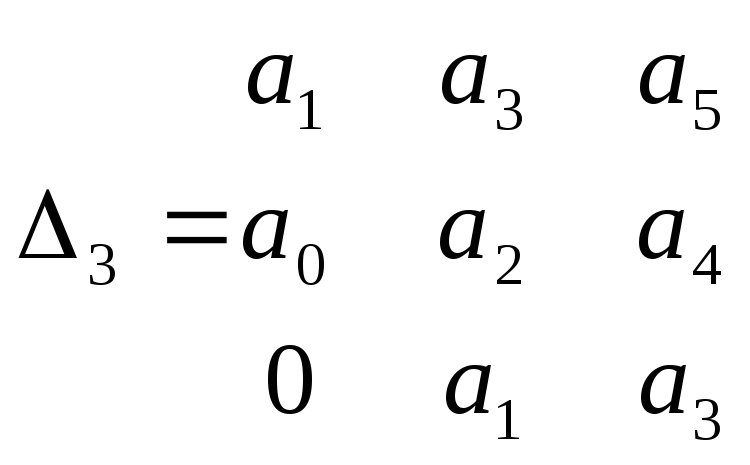Теорема. Для того, чтобы линейная стационарная система была асимптотически устойчива, Н и Д, чтобы при a0>0 все определители Гурвица были положительны (при а0<0 – наоборот). Система находится в состоянии устойчивости, если

и , где i=1,2,…,n-1

Но т.к. , то имеют место 2 случая:

1. - апериодическая граница устойчивости (один из корней хар-го Ур-я =0)

2. - колебательная граница устойчивости (2 комплексно-сопряженных корня хар-го Ур-я, находящихся на мнимой оси)

Частные случаи.

1. Система 1го порядка:

Н=а1 => условие устойчивости : ,

2. Система 2го порядка: :

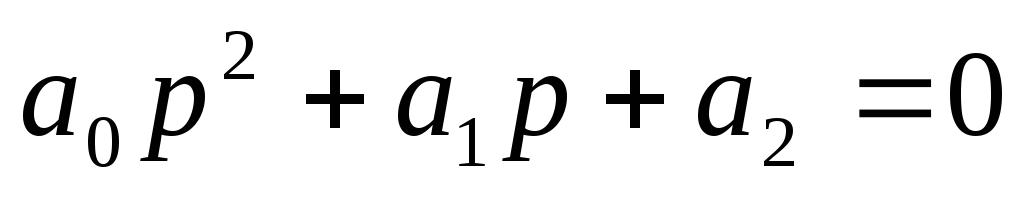; Условие устойчивости: ;; ;

Вывод: для систем 1 и 2 порядка Н иД условием устойчивости является положительность всех к-тов хар-го Ур-я.

3. Система 3го порядка:

; Условие устойчивости: , ;

Из 2х последних Ур-й => . Т.о. для устойчивости системы 3 порядка кроме положительности всех к-тов требуется еще, чтобы , т.е. чтобы произведение средних к-тов хар-го Ур-я было больше произведения крайних.

Частотные критерии устойчивости

Эти критерии базируются на принципе аргумента: изменение аргумента частотного хар-го полинома D(jυ) при изменении частоты 0<υ<∞ равно , где n- порядок системы, m- количество правых корней Ур-я D(p)=0.

Критерий устойчивости А. В. Михайлова (1938г.)

Пусть дано хар-ое Ур-е , тогда хар-ое частотное Ур-е (p=jυ): , где

;

называются соответственно вещественной и мнимой функциями Михайлова.

При изменении частоты υ вектор D(jυ), изменяясь по величине и направлению, будет описывать своим концом в комплексной плоскости некоторую кривую, называющуюся годографом Михайлова.

В соответствии с принципом аргумента, угол поворота вектора D(jυ) вокруг начала координат при изменении частоты υ от 0 до ∞ равен:

- нет правых!

Это условие необходимое, но не достаточное. Для устойчивости Н и Д, все были левыми.

D(jυ), т.о. критерий устойчивости Михайлова: для того, чтобы САУ была устойчива Н и Д, чтобы вектор кривой Михайлова D(jυ) при изменении от 0 до ∞ повернулся, нигде не обращаясь в 0 вокруг начала координат против часовой стрелки на угол πn/2, где n- порядок хар-го Ур-я.

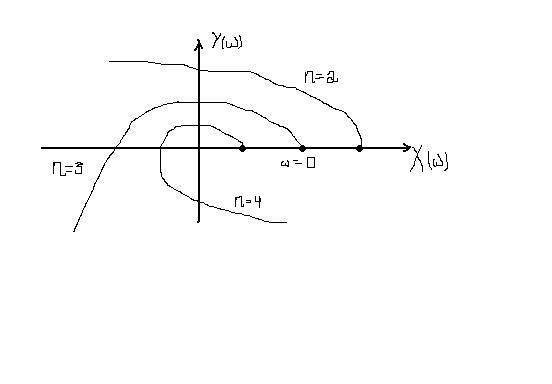
Замечание. Для устойчивых систем кривая Михайлова при υ=0 начинается на положительной вещественной полуоси, т.к. при а0>0 все к-ты хар-го Ур-я положительны (необходимое условие!) => и .

Для устойчивых систем:

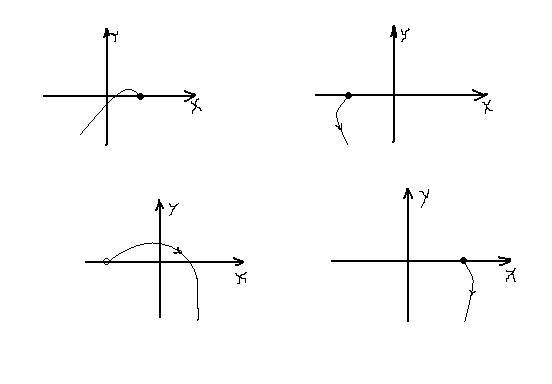
Для неустойчивых систем:

Критерий устойчивости Найквиста

1. Разомкнутая система устойчива

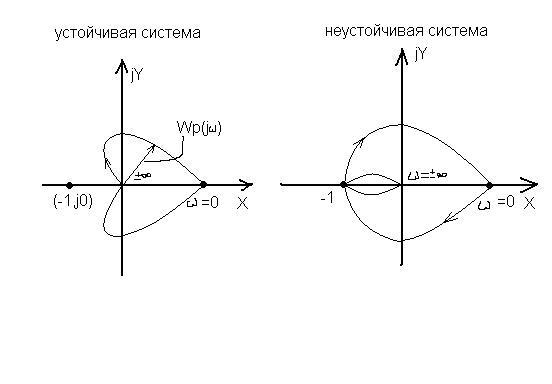
Если разомкнутая система устойчива, то замкнутая САУ также устойчива, если АФЧХ разомкнутой системы W(jυ) не охватывает точку с координатами (-1,j0).

2. Система в разомкнутом состоянии неустойчива

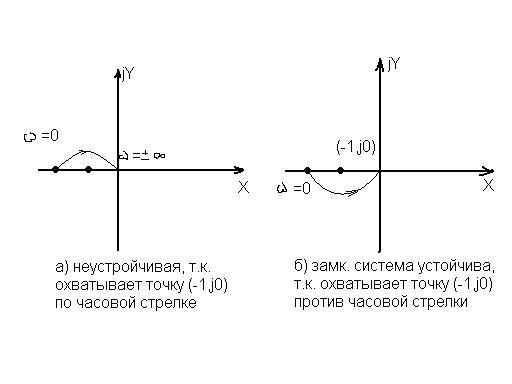
Формулировка критерия: т.о., для устойчивости замкнутой системы, если разомкнутая система неустойчива, Н и Д, чтобы АФХ разомкнутой системы охватывала (при повороте вектора Wp(jυ) против часовой стрелки) точку (-1;j0) столько раз, сколько корней в правой полуплоскости содержит знаменатель передаточной функции разомкнутой системы.

Примеры:

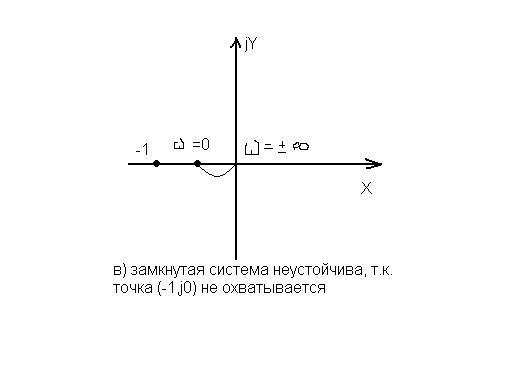
Критерий Найквиста в логарифмической форме

При сложной форме х-ки W(jυ) могут возникнуть затруднения при определении числа ее оборотов вокруг критической точки (-1,j0). В этом случае для суждения об устойчивости удобно применять «правило переходов», предложенное Я.З.Цыпкиным.

Назовем переход хар-ки W(jυ) через отрезок вещественной оси слева от точки (-1,j0), т.е. отрезок (-∞,-1) при возрастании υ положителен, если он проходит сверху вниз, и отрицателен, если снизу вверх. Если х-ка W(jυ) начинается на отрезке (-∞, -1) при υ=0 или заканчивается на нем при υ=∞, то в этих случаях считается, что она совершает полперехода.

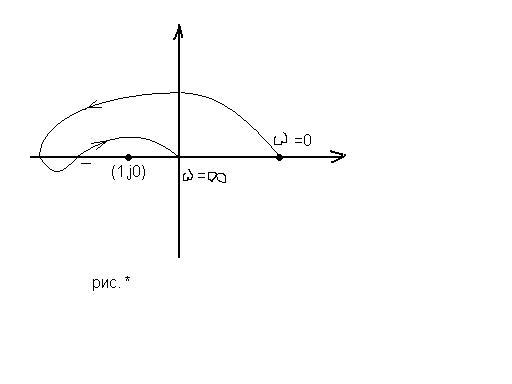
Тогда критерий Найквиста можно сформулировать так: если разомкнутая САУ неустойчива, то для того, чтобы замкнутая САУ была устойчива, Н и Д, чтобы разность между числом положительных и отрицательных переходов АФХ разомк. системы Wp через отрезок вещественной оси (-∞,-1) при изменении частоты υ от 0 до ∞ была равна е/2, где е- число правых корней хар-го Ур-я разомкнутой системы.

Для монотонных ЛАХ и ЛФХ:

Формулировка: если система в разомкнутом состоянии имеет монотонные убывающие ЛАХ и ЛФХ, то для того, чтобы замкнутая САУ была устойчива, Н и Д, чтобы на частоте среза ЛФХ φ(υ) располагалась выше уровня –π.

Показатели качества САУ (временные, частотные, корневые, интегральные). Статическая ошибка и добротность САУ.

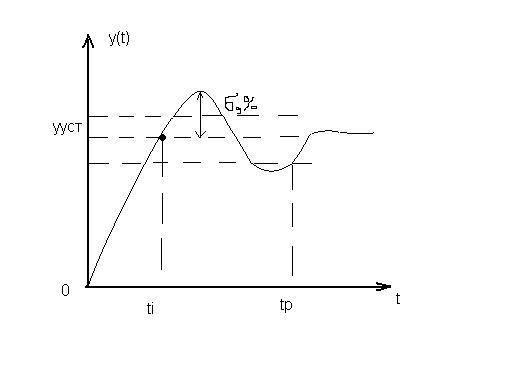
Временные показатели качества являются прямыми оценками качества и определяются по кривой переходного процесса при подаче на вход единичного ступенчатого воздействия.

1) Время переходного процесса (время регулирования) - время вхождения в 5%-зону от уровня установившегося состояния. Чем меньше , тем выше быстродействие системы.

,

2) Перерегулирование σ – это величина максимального отклонения управляемой координаты от установившегося значения, взята в процентах по отношению к уровню установившегося состояния.

3. Установившаяся (статическая) ошибка рассматривается в случае, если установившееся состояние не достигло заданного

4. Время первого согласования (время нарастания) хар-ет быстродействие – минимальное время, при котором система первый раз входит в 5% зону от установившегося состояния.