0491807_F3EAE_lekcii_po_statistike / 008_нормальное_распределение

Тема 8. Нормальное распределение

В 1727 г. Абрахам де Муавр (1667-1754) открыл закон распределения вероятностей, названный законом нормального распределения.

Разработкой вопросов, относящихся к данному закону, занимались Пьер Лаплас (1749-1827) и Карл Гаусс (1777-1855).

Общие условия возникновения закона нормального распределения установил A.M. Ляпунов (1857-1918). Нормальное распределение образуется, если на варьирующую переменную влияет большое число факторов, ни один из которых не имеет преобладающего влияния.

Закон нормального распределения лежит в основе многих теорем и методов статистики при оценке репрезентативности выборки (расчете ошибки выборки и распространении характеристик выборки на генеральную совокупность); измерении степени тесноты связи и составлении модели регрессии; построении и использование статистических критериев и др.

Нормальное распределение

Распределение непрерывной случайной величины х называют нормальным N (х, ), если соответствующая ей плотность распределения выражается формулой:

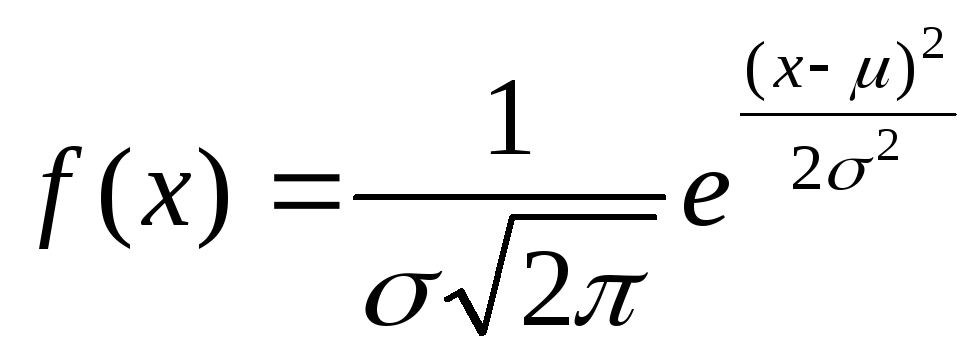
Свойства нормального распределения

1. Значения признака имеют тенденцию концентрироваться около точки t = 0,

где является нормированным отклонением

2. Нормальная кривая симметрична относительно вертикальной оси.

3. Значения наблюдений не ограничены по своей величине.

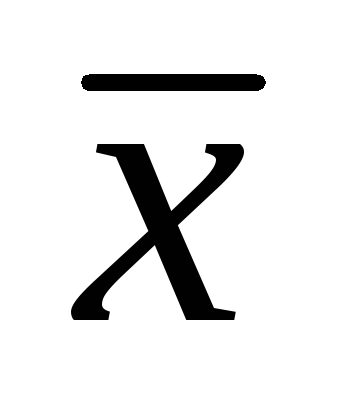4. , и имеют одно и то же значение при t = 0.

5. Изменения величины t характеризует различные типы распределения.

При нормальном распределении значения t колеблются в пределах.

С колебаниями средней величины, кривая нормального распределения будет смещаться по оси абсцисс влево или вправо, тогда как форма кривой останется неизменной.

Косвенные расчеты показателей вариации

Одна из важнейших задач анализа вариационных рядов предполагает выявление закономерностей распределения, определение и построение теоретической формы распределения.

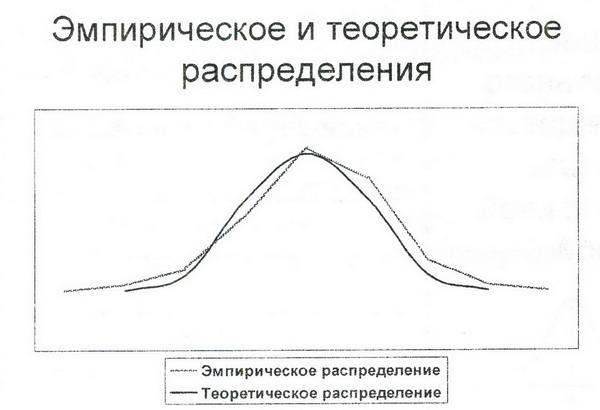
Как показывают многочисленные статистические исследования, частоты (частости) эмпирических распределений за редким исключением будут отличаться от значений теоретического распределения. Расхождения между частотами (частостями) эмпирического и теоретического распределения могут быть несущественными и объяснены случайностями выборки и существенными при несоответствии выбранного и эмпирического законов распределения.

Для проверки гипотезы о соответствии эмпирического распределения теоретическому закону нормального распределения используются особые статистические показатели-критерии согласия (или критерии соответствия). К ним относятся критерии Пирсона, Колмогорова, Романовского, Ястремского и др.

Сравнение эмпирического и теоретического распределения

Производится при помощи критериев соответствия (согласия):

• Критерий К.Пирсона;

• Критерий В.И.Романовского;

• Критерий Б.С.Ястремского;

• Критерий А.Н.Колмогорова.

Критерий согласия К.Пирсона

где m –частота эмпирического распределения, - частота теоретического распределния

Табличное значение хи-квадрат определяется при помощи числа k-числа степеней свободы, равного разности между числом групп (r) и величиной 3 для выравнивания по закону нормального распределения, т.е. k = r- 3.

Если, то расхождения между теоретическим и фактическим распределением считается неслучайным.

Если , то расхождения между теоретическим и фактическим распределением считается случайным, а распределение хорошо согласуется с законом нормального распределения.

Критерий согласия В. И. Романовского

, где k- число степеней свободы

Если R<3, расхождения между теоретическими и эмпирическими частотами считаются случайными,

Если R>3, то неслучайными, существенными.

Критерии согласия Пирсона и романовского не показывают, чем конкретно отличаются рассматриваемые распределения. С этой целью применяются специальные показатели асимметрии и эксцесса.

Критерий согласия Б.С.Ястремского

, где r- число групп.

Величина имеет табличное значение, равное 0,6 для распределений, где число групп представлено до 20.

Если , расхождение между теоретическими и эмпирическими распределениями считаются случайными;

Если , расхождение между теоретическими и эмпирическими распределениями неслучайны, то есть эмпирические распределение не отвечает требованиям нормального распределения.

Критерий согласия А.Н.Колмогорова

Вероятность Р() может изменяться от 0 до 1.

Если принимает значения до 0,3, то Р()=1, следовательно отклонений между эмпирическими и теоретическими частотами нет.