Ф изика термодинамика бля лекции и вопросы / OF3_7_Realnye_gazy_mini_1

3.7.Реальные газы

3.7.1.Реальный газ

3.7.2.Уравнение Ван-дер-Ваальса

3.7.3.Изотермы Ван-дер-Ваальса. Критическое состояние газа

3.7.4.Внутренняя энергия реального газа. Расширение реального газа в вакуум в адиабатических условиях

3.7.5.Эффект Джоуля–Томсона

3.7.6.Сжижение газов

3.7.7.Закон Дальтона для реальных газов

3.7.1. Реальный газ

Реальный газ – газ, в котором существенную роль играет взаимодействие между его молекулами.

Отклонение от закона Бойля– Мариотта

При средних плотностях давление реального газа меньше, чем в случае, когда газ ведёт себя как идеальный. Это объясняется тем, что при средних плотностях проявляются молекулярные силы притяжения, которые делают газ по сравнению с идеальным более сжимаемым под воздействием внешних сил.

При больших плотностях давление реального газа больше того, что можно ожидать от идеального, при этом сжимаемость реального газа меньше сжимаемости идеального. Это объясняется тем, что при больших сжатиях проявляются силы отталкивания (из-за реальных размеров молекул), вследствие чего газ делается менее сжимаемой под действием внешних сил по сравнению с сжимаемостью идеального газа.

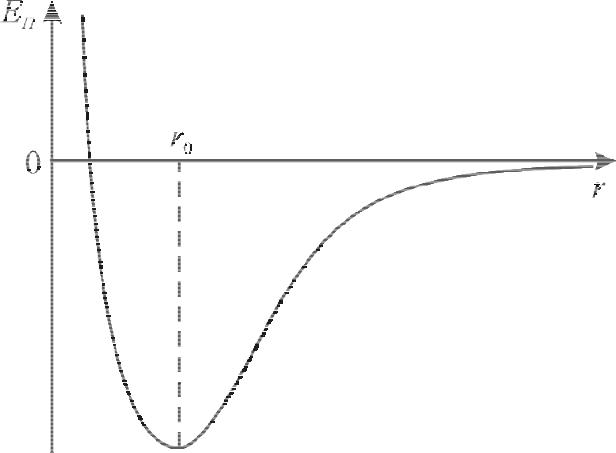
Полная потенциальная энергия системы из двух молекул

Реальный газ

(Real gas)

3.7.2. Уравнение Ван-дерер-- Ваальса

Голландский физик Йоханнес Дидерик Ван-дер-Вáальс (1837-1923) в 1873 г. внёс две поправки в уравнение Клапейрона:

•поправка на внутреннее давление (т. е. на влияние сил межмолекулярного притяжения) a (при этом создаётся дополнительное молекулярное давление p′);

•поправка на собственный объём молекулы

реального газа b.

Тогда уравнение состояния реального газа примет вид:

( p + p′)(V −b) = RT

К выводу значения дополнительного молекулярного давления

Учёт межмолекулярных взаимодействий в реальном газе

Выделим в правой половине объёма одну молекулу. Сила притяжения f, действующая на неё со стороны молекул, находящихся в левой половине объёма, пропорциональна числу молекул в единице объёма (n):

f = C1n

где C1 – константа для данного реального газа.

Дополнительное молекулярное давление p′, действующее на выделенную плоскость, пропорционально силе f и числу молекул, находящихся справа, в единице объёма:

p′ = C2 fn = C2C1n2

Так как число молекул в единице объёма пропорционально плотности газа:

n ~ ρ = m

V

то дополнительное молекулярное давление будет равно:

Итак, как учесть силы притяжения молекул?

Объём недоступности

Эффективный объём, приходящийся на две молекулы Vон называют объёмом недоступности, отнесённым к паре молекул газа.

Полный объём недоступности в одном моле газа равен:

где R = 2r – радиус объёма недоступности или диаметр одной молекулы.