Перейти к оглавлению на странице: 12

ГЛАВА 2. МЕТОД НЬЮТОНА ДЛЯ РЕШЕНИЯ СИСТЕМ НЕЛИНЕЙНЫХ УРАВНЕНИЙ

и предположим, что существует вектор x¯ D Rn , явля-

называется матрицей Якоби, а её определитель – якобианом системы (1.1). Исходное уравнение заменим следующим: F (x0) + F 0(x0)(x − x0) = 0. Считая матрицу Якоби F 0(x0) неособой, разрешим это уравнение относительно x: xˆ = x0 − [F 0(x)]−1F (x0). И вообще положим

При сделанных относительно F (·) предположениях имеет место сходимость последовательности {xk} к решению системы со скоростью геометрической прогрессии при условии, что начальное приближение x0 выбрано из достаточно малой окрестности решения x¯.

При дополнительном предположении F (·) C2[a, b] имеет место квадратичная сходимость метода, т.е.

kxk+1 − x¯k ≤ ωkxk − x¯k2.

7

Перейти к оглавлению на странице: 12

Сформулируем теорему.

Теорема 1.1. Пусть в некоторой окрестности решения x¯ системы (1.1) функции fi(·) C2[a, b] и якобиан системы отличен от нуля в этой окрестности. Тогда существует δ -окрестность точки x¯ такая, что при любом выборе начального приближения x0 из этой окрестности последовательность {xk} не выходит из неё и имеет место квадратичная сходимость этой последовательности.

Замечание 1.1. В качестве критерия окончания процесса итераций обычно берут условие: kxk+1 − xkk < ε.

Замечание 1.2. Сложность метода Ньютона – в обращении матрицы Якоби. Вводя обозначение δxk = xk+1 − xk получаем для вычисления δxk СЛАУ

откуда и находим искомую поправку δxk, а затем и следующее приближение xk+1 = xk + δx к решению x¯. Очевидно, что это значительно сокращает количество арифметических операций для построения очередного приближения.

Замечание 1.3. Начиная с некоторого шага k0 решают стационар-

ную СЛАУ

∂F (xk0 ) · δxk = −F (xk). ∂x

Данное видоизменение носит название модифицированный метод Ньютона.

Замечание 1.4. (О выборе начального приближения). Пусть вектор-функция Φ(λ, x) такова, что Φ(1, x) = F (x), а система Φ(0, x) = 0 может быть решена. Тогда разбивая [0, 1] на N частей решают методом Ньютона набор из N систем

Φ(i/N, x) = 0, i = 1, N,

принимая для каждой следующей системы в качестве начального приближения решение предыдущей системы.

8

Перейти к оглавлению на странице: 12

§2. Пример решения системы методом Ньютона

Рассмотрим задачу решения системы нелинейных уравнений с точностью ε = 0.001:

sin(2x − y) − 1.2x = 0.4; 0.8x2 + 1.5y2 = 1 .

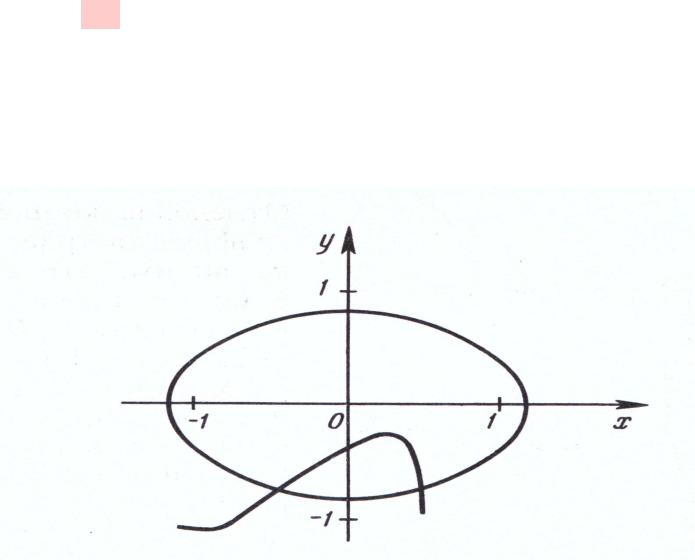
Отделение корней произведём графически (см. рисунок 2).

строим по точкам в диапазоне x [−1.1; +1.1].

Система имеет два решения. Уточним одно из них, расположенное в четвёртой четверти, приняв в качестве начального приближения значения x0 = 0.4; y0 = −0.75.

f1(x, y) = sin(2x − y) − 1.2x − o.4; f2(x, y=0.8x2 + 1.5y2 − 1 .

9

Перейти к оглавлению на странице: 12

Имеем далее:

(f1(x, y))0x = 2 cos(2x − y) − 1.2; (f2(x, y))0x = 1.6x ,

(f1(x, y))0y = − cos(2x − y); (f2(x, y))0y = 3y .

Уточнение корней будем вести методом Ньютона с учётом замечания 1.2:

xn+1 = xn + gn; yn+1 = yn + hn ,

где gn и hn – решение СЛАУ (1.3):

(f1(xn, yn))0xgn + (f1(xn, yn))0yhn = −f1(xn, yn); (f2(xn, yn))0xgn + (f2(xn, yn))0yhn = −f2(xn, yn) .

Отсюда последовательно получаем:

Поскольку три первые знака после запятой установились, процесс вычислений заканчиваем (см. замечание 1.1).

§3. Задания для самостоятельного выполнения

Используя описанный выше метод Ньютона, решить систему нелинейных уравнений с точностью ε = 0.0001, найдя начальное приближение графическим методом и используя замечание 1.2:

10

Перейти к оглавлению на странице: 12

11