параметризация процессов трансформации / lec_4

Расширенное уравнение баланса газовых примесей в атмосфере

Уравнение баланса газовых примесей, полученное из закона сохранения массы, которое в потоковой форме можно переписать в декартовой системе координат виде:

Показывает скорость изменения концентрации газа (молекул в единице объема за единицу времени) в точке пространства за счет адвективного потока массы, т.е. дивергентная изменчивость. В этом уравнении не учитывается локальная и диффузионно-турбулентная изменчивость массы в объеме. Локальная изменчивость может происходить в результате фото- и термодиссоциационных и химических процессов, эмиссий и разрушения на поверхности земли и аэрозолей, фазовых переходов.

Диффузионно-турбулентные процессы приводят к изменению содержания газов за счет хаотичного движения молекул (диффузия), или объемов воздуха (турбулентность), в результате чего происходит перенос массы в направлении выравнивания концентрация (против градиентов).

Для учета этих процессов в расширенном уравнении баланса атмосферных газов в правой части добавляются слагаемые, также как и дивергентные имеющие размерность скорости изменения концентрации (мол/см³с):

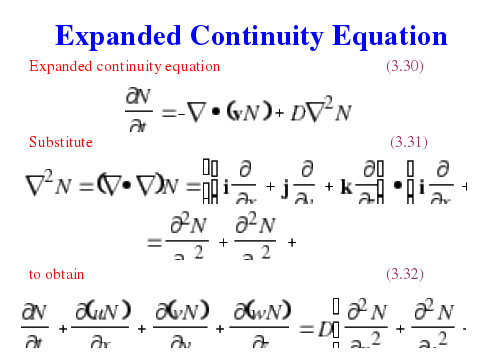
Параметризация химических процессов в моделях газового состава атмосферы

Математическая формулировка задачи базируется на системе уравнений неразрывности многокомпонентной среды при наличии химических реакций:

где - вектор отношений смеси рассматриваемых примесей, N - число рассматриваемых примесей, - линейный дифференциальный оператор, описывающий пространственный перенос примеси, S - скорость фотохимического изменения, которая определяется протекающими в атмосфере процессами фотодиссоциации, бимолекулярными и трехмолекулярными химическими реакциями, мономолекулярным распадом и гетерогенными процессами.

Отношение смеси представляет собой безразмерную величину, соответственно, размерность источникова члена в правой части уравнения будет с^-1 . В химической же кинетике, которая используется для параметризации химических процессов в атмосфере, применяются скорости химических реакций в размерности мол/(см³с). Т.е. химия атмосферы рассматривается в абсолютных единицах, т.к. скорости реакций зависят от концентраций, а не от отношений смеси. Поэтому после параметризации скоростей химических реакций в абсолютных единицах для подстановки в систему уравнений баланса нужно перейти в относительные единицы путем деления на концентрацию воздуха, т.к.

Реакция фотодиссоциации представляет собой первичный процесс, с которого, по сути, начинаются химические реакции в атмосфере. Фотодиссоциация представляет собой реакцию первого порядка вида:

Скорость фотодиссоциации S_i компоненты с концентрацией X_i описывается, согласно реакцией первого порядка в абсолютных единицах:

где J_i - коэффициент фотодиссоциации, концентрация воздуха. Это скорость разрушения и, одновременно, скорость образования и :

Коэффициент фотодиссоциации определяется условиями прохождения солнечной радиации через атмосферу

где - длина волны солнечного излучения,

- спектральная область фотодиссоциации i-й компоненты,

- сечения поглощения,

- квантовый выход реакции,

- суммарный поток радиации с длиной волны в данной точке пространства.

Скорости химических реакций и мономолекулярного распада параметризуются в терминах химической кинетики. При этом скорости бимолекулярных реакций типа

описываются выражением

где - лабораторная константа данной химической реакции, рассчитываемая по формуле Аррениуса:

Здесь A - лабораторная константа, E - энергия активации данной реакции, R - универсальная газовая постоянная, T - температура.

Более сложным образом описываются скорости протекающих в атмосфере трехмолекулярных реакций типа

где M - концентрация воздуха. Фактически эти реакции происходят в два бимолекулярных этапа. Сначала происходит реакция образования промежуточного неустойчивого энергизированного (возбужденного) комплекса:

Далее этот комплекс может или дезактивироваться, или распадся:

Реакции такого типа сильно зависят от давления. При низких давлениях время между столкновениями образующегося на первой стадии реакции возбужденного комплекса с дезактивирующей молекулой больше или сравнимо со временем жизни возбужденного комплекса и реакция является тримолекулярной. При высоких давлениях время между столкновениями мало по сравнению со временем жизни возбужденного комплекса и он успевает дезактивироваться до распада. Реакция при этом является бимолекулярной.

Если скорость реакции образования возбужденного комплекса обозначить , скорость деактивации - , а скорость распада - , то баланс образующейся компоненты определяется по формуле

А концентрация возбужденного комплекса определяется их условия равновесия между продукцией и разрушением:

Откуда можно рассчитать равновесную концентрацию

С учетом этого скорость трехмолекулярной реакции описывается по аналогии с бимолекулярными реакциями:

где к_р описывается универсальной формулой Линдемана-Хиншельвуда [76]:

где

а F₀ , A₀ , , n, m - лабораторные константы данной химической реакции.

Процессы мономолекулярного распада типа

являются обратными по отношению к трехмолекулярным и рассматриваются как реакции второго порядка и их скорости записываются в виде

где k определяется по формуле Аррениуса (1.5).

Гетерогенные процессы на атмосферном аэрозоле в фотохимических моделях описываются уравнениями первого порядка:

Константы гетерогенных реакций k_a вычисляются в предположении свободномолекулярного режима.

Таким образом, слагаемые в правой части системы (1.1), выражающие скорости фотохимического изменения рассматриваемых малых газов, можно записать в виде:

j=1,2,...N,

где члены в правой части с положительным знаком описывают фотохимическую продукцию (за счет химических реакций и фотодиссоциационных процессов), а члены с отрицательным знаком - фотохимическое разрушение (за счет химических реакций, фотодиссоциационных процессов, мономолекулярного распада и гетерогенных процессов).