Параметризация процессов фотодиссоциации в уравнениях баланса газовых примесей

Реакция фотодиссоциации представляет собой первичный процесс, с которого, по сути, начинаются химические реакции в атмосфере. Фотодиссоциация представляет собой реакцию первого порядка вида:

Скорость локального процесса фотодиссоциации - , входящая в правую часть полученного ранее расширенного уравнения баланса газовой примеси, для газовой компоненты с концентрацией описывается, реакцией первого порядка в единицах мол/см³с:

где J_i - коэффициент фотодиссоциации (единицы с^-1), -концентрация газовой компоненты, которая при поглощении фотонов солнечного света может распасться на и . Это - скорость разрушения , т.е входит с отрицательным знаком в уравнение баланса -й примеси, и, одновременно, скорость образования и (входит с положительным знаком в их уравнения баланса):

Коэффициент фотодиссоциации определяется условиями прохождения солнечной радиации через атмосферу и радиационными свойствами поглощающего радиацию газа

где - длина волны солнечного излучения,

- спектральная область, в которой i-я компонента может фотодиссоциировать при поглощении фотонов света с длинами волн из этого интервала,

- сечение поглощения, которое определяет способность газа i поглощать радиацию с длиной волны ,

- квантовый выход реакции фотодиссоциации, который определяет вероятность распада газа i на газы l и m после поглощения фотона света с длиной волны .

- суммарный поток радиации с длиной волны на высоте в данной точке пространства.

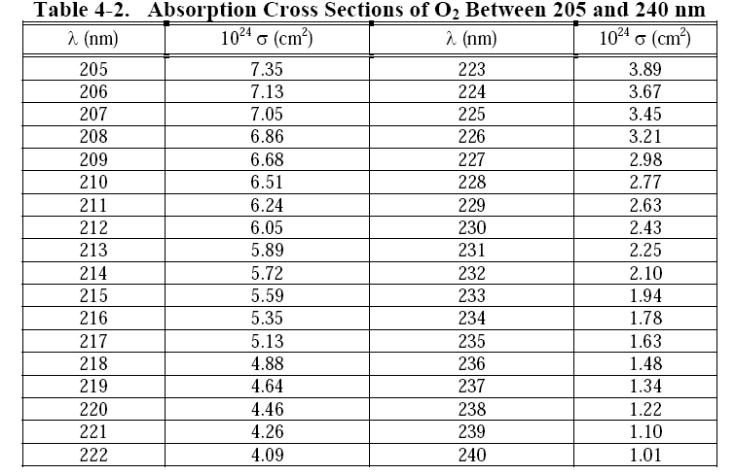
Поглощающие свойства газов описываются сечениями поглощения и квантовыми выходами, которые измеряются в лабораторных экспериментах и приводятся в сборниках рекомендованных для атмосферных процессов реакциях вместе с параметрами химических реакций, таких как JPL (http://jpldataeval.jpl.nasa.gov/). Ниже приведен пример сечений поглощения для молекулярного кислорода в интервале длин волн от 205 до 240 нм.

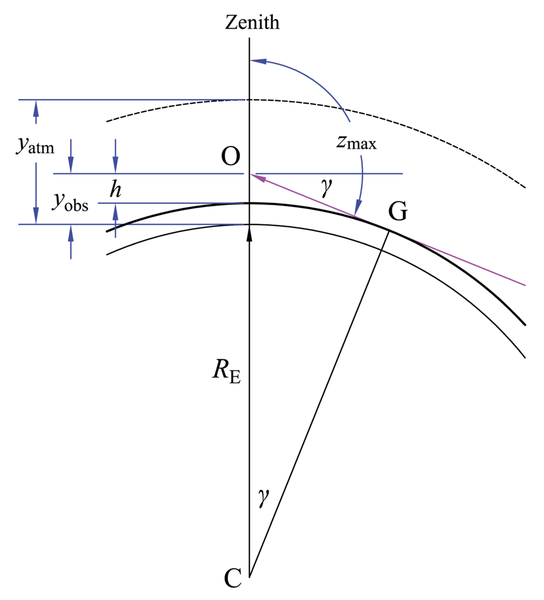
Поток солнечной радиации на данной высоте в данной географической точке зависит от условий прохождения солнечной радиации через атмосферу, ее отражения земной поверхностью, поглощения и рассеяния атмосферными газами и аэрозолей.

Распространене солнечной радиации в Земной атмосфере

Попадающая на верхнюю границу атмосферы солнечная радиация ослабляется в ней в соответствии с законом Бера-Ламберта, который определяет ослабление падающего излучения бесконечно тонким слоем :

Где - коэффициент ослабления, определяемый процессами поглощения и рассеяния радиации с длиной волны слоем . Это уравнение показывает, на сколько уменьшается (знак минус в правой части) поток радиации при прохождении ею слоя , свойства которого ослаблять радиацию описываются коэффициентом .

Если слой имеет конечную толщину , а радиация проходит через него под прямым углом, то ослабление радиации при прохождении этого слоя определяется интегрированием уравнения Бера-Ламберта,

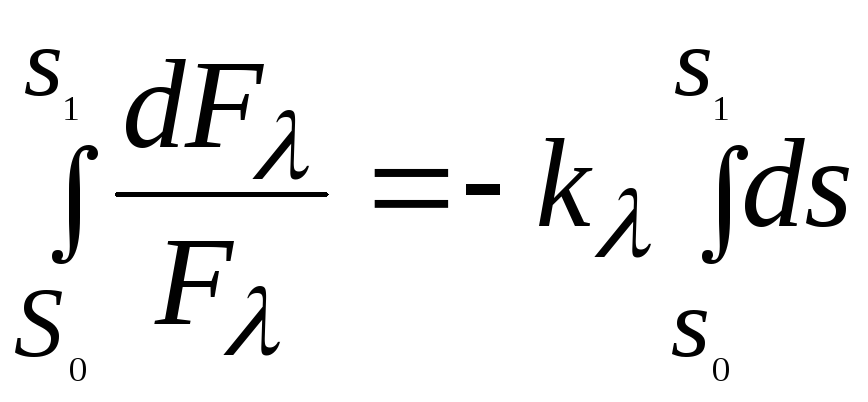
в результате чего получается закон Бугера:

Если в качестве направления выбрать высоту в атмосфере (z), а значения спектрального потока солнечной радиации на верхней границе атмосферы обозначить , то поток прямого солнечного излучения на высоте z в соответствии с законом Бугера будет

Где - оптическая толщина слоя выше уровня z.

Оптическая толщина слоя определяется его поглощающими свойствами и геометрией прохождения солнечного луча через атмосферу, т.к. поток солнечных фотонов падает на верхнюю границу атмосферы, как правило, не под прямым углом, а под углом, определяемым высотой солнца, или зенитным углом.

Высота солнца – это угол солнца над горизонтом, а зенитный угол – это угол от направления в зенит. В сумме они составляют 90^О.

Таким образом, оптическая толщина вычисляется как

Где представляет собой оптическую массу атмосферы, показывающую, во сколько раз увеличивается путь солнечного луча в атмосфере при зенитном угле по сравнению с нулевым зенитным углом. Интегрирование по высоте необходимо в связи с изменчивостью свойств ослабления атмосферы с высотой.

Решая геометрическую задачу в предположении плоско-параллельной атмосферы получаем выражение для массы атмосферы в зависимости от зенитного угла Солнца:

Если учитывать сферичность Земли и атмосферы, то оптическая масса вычисляется по боле сложной формуле

С учетом распространения солнечного луча в феерической атмосфере