Формулировка алгоритма фильтра Калмана

Рассмотрим сначала линейную задачу, т.е. вариации модельных предсказаний в окрестности предсказания являются линейной функцией начального состояния, т.е. для всякого , достаточно близкого к

Модель использует данные анализа на сетке в момент времени для того, чтобы вычислить прогностические значения на той же сетке в момент времени:

Предполагается, что модель может быть несовершенной и давать некоторую ошибку:

Из практики можно предположить, что ошибки не имеют сдвига и не коррелируют во времени:

где - символ Кронекера, равный 1 прии 0 при всех прочих случаях.,- матрица ошибок модели в момент времени. Определим ошибку анализа в момент времени:

и вычислим ошибку прогноза с учетом линейности оператора моделирования

Возводя вквадрат, т.е., умножая левую часть на , а правую на, и полагая, что ошибки моделирования не коррелируют с ошибками анализа, т.е., получаем

где - ковариационная матрица ошибок прогноза в момент времени, а- ковариационная матрица ошибок анализа в момент времени.

В результате получены два прогностических уравнения для момента времени на основании значений в момент времени: одно позволяет прогнозировать значение вектора состояния, а второе ковариационную матрицу ошибок прогноза. Таким образом, использование методики фильтра Калмана позволяет рассчитывать как прогностические значения вектора состояния, так и ковариационную матрицу ошибок прогноза. Ковариационные матрицы ошибок прогноза и анализа являются идентичными матрицам ошибок оценки фонового состоянияи анализа.

Прогностическая часть алгоритма должна быть дополнена уравнениями для вычисления результатов анализа вектора состояния, матрицы преобразования весов, а также ковариационной матрицы ошибок анализа. Эти уравнения аналогичны выведенным при рассмотрении обобщенного метода оптимальной интерполяции:

Эти три уравнения представляют собой аналитическую часть метода фильтра Калмана, а уравнения для прогноза вектора состояния и ковариационной матрицы ошибок – прогностическую часть фильтра Калмана.

Если у нас есть результаты измерений , ошибки измерений, и ошибки моделирования, то начиная с начального момента времени, если определеныи, то можно вычислить значения анализа в этот момент времении ошибки анализа. Затем, используя прогностические уравнения, можно вычислить для следующего момента времени прогностические значения вектора состоянияи ковариационную матрицу ошибок прогноза. После этого последовательность повторяется, т.е. вычисляютсяии т.д для последующих моментов времени.

Фильтр Калмана аналогичен оптимальной интерполяции в части анализа и четырехмерному вариационному анализу в прогностической части, если не учитывается ошибка моделирования.

Расширенный фильтр Калмана

Если оператор модели нелинеен, то используется расширенный фильтр Калмана, в котором оператор линеаризуется в окрестности анализируемого вектора состояния, а оператор наблюдений линеаризуется около. Таким образом, подразумевается, что

Это означает, что при вычислении ошибки прогноза мы должны учитывать Якобиан оператора моделирования:

Соответственно, прогностическое уравнение для ковариационной матрицы прогноза будет выглядеть как

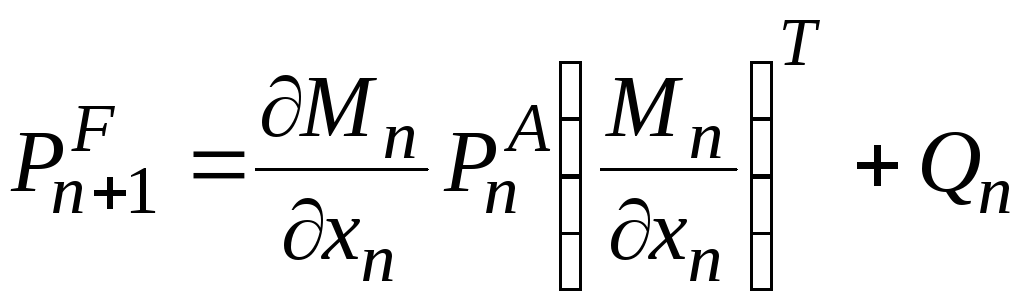
Вычислительная стоимость фильтра Калмана и его расширенного варианта получается достаточно большой, т.к. помимо собственно анализа, который, как было определено при исследовании оптимальной интерполяции, занимает много процессорного времени и памяти, нужно еще оценивать матрицы ковариаций анализа, делать прогноз вектора состояния, вычислять Якобиан для нелинейной модели и прогноз изменения матрицы ковариаций анализа. В результате вычислительная стоимость фильтра Калмана намного больше 4-мерного вариационного для той же задачи, даже для малых моделей.

Схема организации вычислений в фильтре Калмана