
- •Проверка статистических гипотез
- •Статистические гипотезы
- •1. Простые и сложные гипотезы и их проверка
- •2. Критерий согласия Пирсона
- •Поведение , когда гипотезаверна.
- •Поведение , когда гипотезаневерна.
- •Критерий проверки.
- •Границы применимости критерия на практике.
- •3. Критерий согласия для сложных гипотез
- •4. О критериях согласия Колмогорова и Смирнова
- •5. Проверка нормальности при помощи вероятностной бумаги
- •Статистические критерии.
- •[Править] Уровень значимости и мощность.
- •[Править] Состоятельность и несмещенность критериев.
- •[Править] Некоторые типовые задачи прикладной статистики [править] Статистические данные и прикладная статистика
- •[Править] Статистический анализ точности и стабильности технологических процессов и качества продукции
- •[Править] Задачи одномерной статистики (статистики случайных величин)
- •[Править] Непараметрическое оценивание математического ожидания.
- •[Править] Непараметрическое оценивание функции распределения.
- •[Править] Таблица 1
- •[Править] Проблема исключения промахов.
- •[Править] Многомерный статистический анализ
- •[Править] Корреляция и регрессия.
- •[Править] Дисперсионный анализ.
- •[Править] Методы классификации.
- •[Править] Дискриминантный анализ.
- •[Править] Кластер-анализ.
- •[Править] Задачи группировки.
- •[Править] Снижение размерности.
- •[Править] Статистика случайных процессов и временных рядов
- •[Править] Статистика объектов нечисловой природы
- •Лабораторная работа №14. Изучение критериев Колмогорова и омега-квадрат
- •Лабораторная работа №15. Изучение критерия хи-квадрат Пирсона
[Править] Проблема исключения промахов.
При первичной обработке статистических данных важной задачей является исключение результатов наблюдений, полученных в результате грубых погрешностей и промахов. Например, при просмотре данных о весе (в килограммах) новорожденных детей наряду с числами 3,500, 2,750, 4,200 может встретиться число 35,00. Ясно, что это промах, и получено ошибочное число при ошибочной записи — запятая сдвинута на один знак, в результате результат наблюдения ошибочно увеличен в 10 раз.
Статистические методы исключения резко выделяющихся результатов наблюдений основаны на предположении, что подобные результаты наблюдений имеют распределения, резко отличающиеся от изучаемых, а потому их следует исключить из выборки. Простейшая вероятностная модель такова. При нулевой гипотезе результаты наблюдений рассматриваются как реализации независимых одинаково распределенных случайных величин X1,X2,...,Xnс функцией распределенияF(x). При альтернативной гипотезеX1,X2,...,Xn − 1— такие же, как и при нулевой гипотезе, аXnсоответствует грубой погрешности и имеет функцию распределенияG(x) =F(x−c), гдеcвелико. Тогда с вероятностью, близкой к 1 (точнее, стремящейся к 1 при росте объема выборки),
![]() ,
,
то есть при описании данных в качестве возможной грубой ошибки следует рассматривать Xmax. Критическая область имеет вид
![]() .
.
Критическое значение d=d(α,n) выбирают в зависимости от уровня значимости ? и объема выборки n из условия
![]() .
(1)
.
(1)
Условие (1) эквивалентно при больших nи малых α следующему:
![]() (2)
(2)
Если функция распределения результатов наблюдений F(x) известна, то критическое значениеdнаходят из соотношения (2). ЕслиF(x) известна с точностью до параметров, например, известно, чтоF(x) — нормальная функция распределения, то также разработаны правила проверки рассматриваемой гипотезы[7].
Однако часто вид функции распределения результатов наблюдений известен не абсолютно точно и не с точностью до параметров, а лишь с некоторой погрешностью. Тогда соотношение (2) становится практически бесполезным, поскольку малая погрешность в определении F(x), как можно показать, приводит к большой погрешности при определении критического значенияdиз условия (2), а при фиксированномdуровень значимости критерия может существенно отличаться от номинального[2].
Поэтому в ситуации, когда о F(x) нет полной информации, однако известны математическое ожиданиеM(X) и дисперсия σ2=D(X) результатов наблюденийX1,X2,...,Xn, можно использовать непараметрические правила отбраковки, основанные на неравенстве Чебышёва. С помощью этого неравенства найдем критическое значениеd=d(α,n) такое, что
![]() .
.
Так как
![]() ,
,
то соотношение (3) будет выполнено, если
![]() .
(4)
.
(4)
По неравенству Чебышёва
![]() ,
(5)
,
(5)
поэтому для того, чтобы (4) было выполнено, достаточно приравнять правые части формул (4) и (5), то есть определить dиз условия
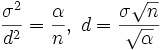 .
(6)
.
(6)
Правило отбраковки, основанное на критическом значении d, вычисленном по формуле (6), использует минимальную информацию о функции распределенияF(x) и поэтому исключает лишь результаты наблюдений, весьма далеко отстоящие от основной массы. Другими словами, значениеd1, заданное соотношением (1), обычно много меньше, чем значениеd2, заданное соотношением (6).
