
ОСАПР / Лабораторный_практикум_ОСАПР
.pdf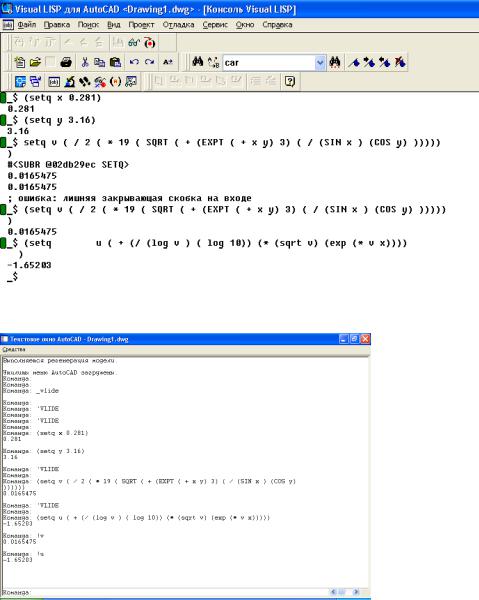
•«ALT+2» - окно «Трассировки»;
•«ALT+3, 4, 5…» - окно соответственно первого, второго, третьего… программных текстов (файлов) в алфавитном порядке.
4.Непосредственный набор программы AutoLISP в командной строке AutoCAD (см рис. 10.2).
В ответ на приглашение:
Команда:
набираются команды языка и последовательно выполняются.
Для перехода в AutoCAD из графического режима в текстовое окно
иобратно достаточно нажать клавишу F2.
Рисунок 10.1 Вычисление выражения в режиме Консоль
Рисунок 10.2 Непосредственный набор программы в AutoCAD
5. Набор Лисппрограммы в редакторе VisualLISP (см рис. 10.3).
171

Рисунок 10.3 Лисп –программа
6.Задача на этом этапе освоения VisualLISP начать изучать справочник операторов. Нажать клавишу F1. Все операторы упорядочены по алфавиту.
7.Сохранить набранную программу: Файл/Сохранить как… указать путь, дать имя файлу, которое необязательно должно совпадать с именем функции, расширение файла *.lsp.
Для запуска программы необходимо изучить панель «Инструменты».
На ней всего девять кнопок, по умолчанию панель расположена слеваот текстового поля.
Кнопки панели «Инструменты»
загрузка содержимого всего текущего файла в оперативную память



 то же для выделенного фрагмента файла
то же для выделенного фрагмента файла



 проверка синтаксиса во всём файле
проверка синтаксиса во всём файле



 то же для выделенного фрагмента файла
то же для выделенного фрагмента файла



 форматирования всего кода
форматирования всего кода



 то же для выделенного фрагмента файла
то же для выделенного фрагмента файла 


 комментирование выделенного фрагмента кода
комментирование выделенного фрагмента кода
раскомментирование выделенного фрагмента кода



 "быстрая справка"
"быстрая справка"
172
8.Нажать первую кнопку (загрузка содержимого всего текущего файла в оперативную память). После в автоматически открывшейся консоли набираем имя нашей функции в круглых скобках (prim1) и следуем указаниям в командной строке.
9.Загрузка и выполнения программы в AutoCAD
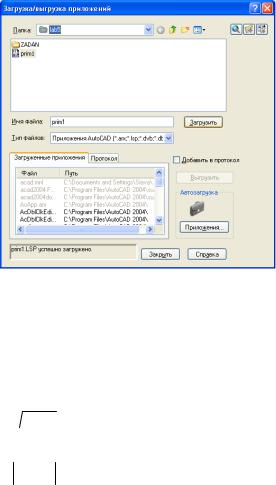
В AutoCAD выбрать из меню Сервис пункт AutoLISP/Загрузить.. (см рис. 10.4), затем в диалоговом окне «Загрузка/выгрузка приложений» найти файл, необходимый для загрузки и нажать кнопку «Загрузить», а затем «Закрыть». Затем в командной строке набираем имя нашей функции в круглых скобках (prim1) и следуем указаниям в командной строке.
Рисунок 10.4 Диалоговое окно загрузки приложений
II Разветвляющееся алгоритмы.
Используя функции IF, COND, написать лисп-программы вычисления заданной функции и номер формулы
 x + 2 , y = x −1 ,
x + 2 , y = x −1 ,
x2 + 4
если x ≥ 7 или x = −1 |
(1) |
если 0 < x < 7 |
(2) |
в ост. случаях |
(3) |
На рис. 10.5 и рис. 10.6 приведены соответствующие тексты программ
173

Рисунок 10.5 Пример использования функции IF
Рисунок 10.6 Пример использования функции COND
ТРЕБОВАНИЕ К ОТЧЕТУ
Отчет должен содержать титульный лист с названием лабораторной работы и включать следующие разделы.
1.Цель работы.
2.Линейный алгоритм
• вычисление выражения в режиме «Консоль» (копия экрана);
174
•непосредственный набор программы в AutoCAD (копия экрана);
•лисп-программа: отладка в режиме «Консоля» (копия экрана) и загрузка программы в AutoCAD (копия экрана).
3.Разветвляющийся алгоритм
•лисп-программа с использованием функции IF: отладка в режиме «Консоля» (копия экрана) и загрузка программы в AutoCAD (копия экрана);
•Лисп-программа с использованием функции COND: отладка
в режиме «Консоля» (копия экрана) и загрузка программы в AutoCAD (копия экрана).
Примечание Варианты индивидуальных заданий выбираются по списку студентов в журнале из таблиц 10.1 и 10.2.
Таблица 10. 1 Задания линейных алгоритмов
Вари- |
Вид функции |
Вари |
Вид функции |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
ант |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ант |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
b = |
1 |
+cos2 (x + z) |
16 |
b = x + |
|
|
|
3 |
zy |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
x |
3 |
|
−2y |
2 |
|
|
|
|
y |
+ cos x |
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
b = |
|
|
|
|
ln2 |
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x−y |
|
|
|
|
|
|
|
|
|
y |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
2 |
|
|
|
|
|
x |
|
+ |
|
y |
|
|
|
17 |
b =lg |
|
|
|
e |
|
|
+ x |
|
|
|
+ z |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
3 |
b = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y3 |
|
|
|
|
18 |
b =1+ |
|
x2 +1 |
+sin 2z |
|||||||||||||||||||||||||||||||
|
|
x + y3 cos2 z |
3 + y2 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
4 |
b = |
|
|
|
|
|
|
x + 4 |
|
y |
|
+cos2 z |
19 |
b = |
|
cos x +cos y |
|
+ 2sin2 z |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
5 |
|
3 |
|
|
esin x |
|
|
cos y |
20 |
b = |
ln(y3 )(z − x / 2) |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
b = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 cos2 x |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
z2 |
+1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
6 |
b = z(tg y −e−(x+3)) |
21 |
b = 10(3 z + x(y+2)) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
7 |
b = |
|
x−y |
|
|
(sin2 z +tg z) |
22 |
b = (sin z)2 |
|
+ |
|
|
x + y |
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
8 |
b = y +3 x −1+ 2z |
23 |
b = e2z −3 y |
|
x |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
9 |
b = x(tg z +cos2 y) |
24 |
b = e(x−1) +sin y |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
10 |
b = e |
|
x−y |
|
|
(tg 2 z +1)x |
25 |
b = |
|
z |
|
e−(y+x / 2) |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
175

Вари- |
Вид функции |
|
|
|
|
|
Вари |
Вид функции |
|
|
|
|
|||||||||||||||||||||||
ант |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ант |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11 |
b = cos |
2 |
z |
+tg 2x + |
|
y |
|
26 |
b = |
4y2e2 x sin 2 z |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
3z3 +ln x |
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
12 |
b = 5tg z −4y2 + |
|
xy |
|
|
|
|
27 |
b = |
|
|
|
y ln x − z x2 |
|
x |
||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
1 +tg 2 x2 |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
13 |
b = (z − x) |
|
y −lnz |
|
|
|
|
|
28 |
b = |
|
lg(y + z + x2 ) |
|||||||||||||||||||||||
|
+(y − x) |
2 |
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
y + x2 |
|
|
|
|
|||||||||||||||
14 |
b = y |
z |
+ |
|
|
x |
|
+ |
|
y |
|
|
|
|
|
29 |
b = |
|
|
x2 + 4 |
|
y |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
sin 2 z 2 |
+ x / 2 |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
15 |
b = |
lg( |
|
x + |
|
y + 2) |
|
|
|
|
|
30 |
b = |
sin x + |
|
z − y |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
2z |
|
|
|
|
|
|
|
|
|
|
|
|
|
y(x − 2)+ x2 |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 10.2 Варианты заданий разветвляющегося процесса
ВариВид функции ант
|
1/ x, |
|
|
если x ≥ −5, x ≠ 0 |
(1) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 , |
|
|
|
|
если x ≤ −10 |
(2) |
|||
y = x |
|
|
|
|
|||||||
|
|
|
x +1 |
|
в ост. случаях |
(3) |
|||||
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
, |
|
|
|
|
если x ≤ 0, x ≠ −10 |
(1) |
||
2 |
x |
|
|
|
|
|
|
||||
y = |
|
x +1, |
если x >1 |
|
(2) |
||||||
|
|
|
|
|
|
|
|
|
в ост. случаях |
(3) |
|
|
1/ x |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 x |
|
|
|
|
|
x +e |
, |
если x ≤ 0, |
x ≠ −1 |
(1) |
||||||
3 |
|
||||||||||
y = cos2 |
x, |
если 0 < x ≤ 3,14 |
(2) |
||||||||
|
x |
|
|
|
|
|
|
|
в ост. случаях |
(3) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
, |
|
|
|
|
если x >1, |
x ≠ 20 |
(1) |
|
4 |
x |
|
|
|
|
||||||
y = x2 , |
|
|
если −5 ≤ x ≤ 5 |
(2) |
|||||||
|
|
|
|
x |
|
|
|
|
в ост. случаях |
(3) |
|
|
|
|
|
|
|
|
|||||
|
lg |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
||||
|
|
|
x, |
|
|
если x ≥100, x ≠105 |
(1) |
||||
5 |
|
|
x, |
|
|
если x = 20 или x = 40 |
(2) |
||||
y = 3 |
|
|
|
||||||||
|
|
2 |
+1 |
|
в ост. случаях |
(3) |
|||||
|
x |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
176

Вари- |
|
|
|
|
|
Вид функции |
|
|
||||||||||||
ант |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
x, |
|
|
|
|
если x > 2 |
|
(1) |
|||||||||||
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
если x ≤ 2 и x ≠ 0 |
|
(2) |
||||
y = 1/ x, |
|
|
|
|
|
|||||||||||||||
|
|
2 |
|
−1 |
|
|
|
|
в ост. случаях |
|
(3) |
|||||||||
|
x |
|
|
|
|
|
|
|
||||||||||||
|
8x +1, |
|
|
|
|
если x ≥ 5, x ≠ 9 |
|
(1) |
||||||||||||
7 |
|
2 |
|
+ |
|
x |
|
, |
|
если x ≤1 |
|
(2) |
||||||||
y = x |
|
|
|
|
|
|||||||||||||||
|
|
3 + |
|
|
|
|
|
x |
в ост. случаях |
|
(3) |
|||||||||
|
x |
|
|
|
|
|
|
|||||||||||||
|
1−3x, |
|
|
|
|
если x > 0, x ≠ 8 |
|
(1) |
||||||||||||
8 |
|
2 |
|
−sin x, |
если x ≤1 |
|
(2) |
|||||||||||||
y = x |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
в ост. случаях |
|
(3) |
||||
|
cos x |
|
|
|
|
|
||||||||||||||
|
|
3 |
|
+1, |
|
|
|
|
|
|
|
если x ≥ 8, x ≠10 |
|
(1) |
||||||
9 |
x |
|
|
|
|
|
|
|
|
|
|
|||||||||
y = 2x2 + 3 x, |
если x ≤1 |
|
(2) |
|||||||||||||||||
|
|
x |
|
|
|
|
|
|
|
|
|
|
в ост. случаях |
|
(3) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
x, |
|
|
|
|
если x ≥ 4 |
|
(1) |
|||||||||||
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
если x ≤1 |
|
(2) |
||||
y = 2x +3, |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
x3 −4 |
|
|
|
|
|
|
в ост. случаях |
|
(3) |
||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
2 |
2x, |
если x ≥ 5 |
(1) |
|
|||||||||||||
11 |
lg |
|
|
|||||||||||||||||
y = 2x2 , |
|
|
|
|
если x < −2 |
(2) |
|
|||||||||||||
|
sin x |
|
|
|
|
в ост. случаях |
(3) |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
x, |
|
|
|
|
если x ≥ 4, или x =1 |
(1) |
||||||||||||
12 |
|
|
x +1, |
если x ≤ −2 |
|
(2) |
||||||||||||||
y = ln |
|
|||||||||||||||||||
|
e− |
x |
|
|
|
|
|
|
|
|
|
|
в ост. случаях |
|
(3) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
x / 3 , |
|
|
|
|
если −3 ≤ х ≤ 3 |
(1) |
|||||||||||||
13 |
|
|
|
|
|
|
|
|
|
+1) , |
если x < −3 |
|
(2) |
|||||||
y = lg (х2 |
|
|||||||||||||||||||
|
|
x3 −2 |
в ост. случаях |
|
(3) |
|||||||||||||||
|
|
|
||||||||||||||||||
|
|
|
|
x3 + 4 |
|
|
, |
если x ≤ −1 или x = 0 (1) |
||||||||||||
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
14 |
|
|
x / 2, |
|
|
|
|
если x ≥ 8 |
|
(2) |
||||||||||
y = |
|
|
|
|
|
|
||||||||||||||
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
в ост. случаях |
|
(3) |
||||
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
3x2 + 4, |
если x ≥ 2 |
|
(1) |
|||||||||||||||
15 |
|
|
x −2 |
|
, |
если x < 0 |
|
(2) |
||||||||||||
|
|
|
||||||||||||||||||
y = ln |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
в ост. случаях |
(3) |
|||||
|
cos x |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
177

Вари- |
|
|
|
|
Вид функции |
|
|
|
|||||||||||||||||
ант |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
tg x / 2, |
|
|
|
|
|
|
|
|
если 0 < x ≤ 2 |
|
(1) |
|||||||||||||
16 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
если x ≤ 0 |
(2) |
|||
y = x2 +1, |
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
x |
|
|
|
|
|
|
|
|
в ост. случаях |
(3) |
|||||
|
cos |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
x |
2 |
|
−2x, |
|
|
|
если x ≥10 |
|
(1) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
17 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
если x ≤1 |
|
(2) |
||
y = ex / 2 , |
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
/ 4 |
|
|
в ост. случаях |
|
(3) |
||||||
|
ln x + x |
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
2 x |
, |
|
|
|
|
|
|
|
|
|
|
|
|
если x ≤ 0 |
|
(1) |
|||||||
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
18 |
|
|
|
|
x2 |
|
|
−2 |
|
, |
|
|
|
|
если 0 < x < 7 |
|
(2) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
y = |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
/ 2 − x2 |
|
|
|
|
|
в ост. случаях |
|
(3) |
|||||||||||||||
|
x |
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
e2 x , |
|
|
|
|
|
|
|
|
если x ≥ 0 |
(1) |
|||||||||||||
19 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
если x < −1 |
(2) |
|||
y = cos x / 3, |
|
|
|
|
|
||||||||||||||||||||
|
|
|
x +1 |
|
|
|
|
|
|
|
|
|
|
в ост. случаях |
(3) |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
x / 3 + x2 , |
|
|
|
если 0 ≤ x ≤ 3 |
(1) |
|||||||||||||||||||
20 |
|
|
x |
|
+3 , |
|
|
|
|
|
|
|
|
если x < 0 |
(2) |
||||||||||
y = |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
2x |
|
|
|
|
|
|
|
|
|
|
|
в ост. случая |
(3) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
x +1, |
|
|
|
|
|
|
|
|
если x ≥ 8, x ≠10 |
|
(1) |
|||||||||||
21 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
если 0 < x < 8 |
|
(2) |
||
y = 0,6x, |
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
x |
|
+3 |
|
|
|
|
|
в ост. случаях |
|
(3) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
lg |
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
2 |
, |
|
|
|
|
|
|
|
|
|
|
|
если x > 0, x ≠ 3 |
|
(1) |
||||
|
2x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
22 |
|
|
x2 |
+1 |
|
|
|
|
|
|
|
|
если x ≤ −2 |
|
(2) |
||||||||||
y = |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
x +5 |
|
|
|
|
|
|
|
|
|
в ост. случаях |
|
(3) |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x −1, |
|
|
|
|
|
|
|
|
если x ≥10, x ≠ 20 |
(1) |
||||||||||||
23 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
если x < 0 |
|
(2) |
||
y = 1/ x +e2 x , |
|
|
|
|
|||||||||||||||||||||
|
ln (x +1) |
|
|
|
|
|
в ост. случаях |
|
(3) |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
2x − x2 |
−1 |
|
, |
если x ≤ −1, x ≠ −4 |
(1) |
|||||||||||||||
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
24 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
если x > 0 |
|
(2) |
||
y = ln (x +3), |
|
|
|
|
|||||||||||||||||||||
|
|
/ 2 |
|
|
|
|
|
|
|
|
|
|
|
|
в ост. случаях |
|
(3) |
||||||||
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
2 |
|
|
|
x / 2, |
|
|
|
если x > 3 |
|
(1) |
|||||||
25 |
cos |
|
|
|
|
|
|
|
|
||||||||||||||||
y = lg |
2x + 4 |
|
|
|
|
если −2,5 ≤ x ≤ 3 |
(2) |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
в ост. случаях |
|
(3) |
||
|
3/ x |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
178
Вариант
26
27
28
29
30
|
|
|
|
Вид функции |
|
|
|
||||
|
|
−x |
+1, |
если x ≥1 |
(1) |
|
|||||
|
e |
|
|
|
|||||||
y = |
lg 2x, |
если1 < x ≤ 5 |
(2) |
|
|||||||
|
|
2 |
|
|
|
в ост. случаях |
(3) |
|
|||
|
x |
|
|
|
|
|
|
||||
|
|
|
2 |
x / 2, |
если x > 0, x ≠ 2 |
(1) |
|
||||
|
lg |
|
|
||||||||
y = |
|
|
|
|
|
|
если x ≤ −1 |
(2) |
|
||
2ex+1 , |
|
||||||||||
|
|
5 + x2 |
в ост. случаях |
(3) |
|
||||||
|
|
|
|||||||||
|
x3 / 2, |
если x > 0, x ≠ 2 |
(1) |
|
|||||||
y = |
|
|
|
|
|
|
если x ≤ −1 |
(2) |
|
||
2ex+1 , |
|
||||||||||
|
|
5 + x2 |
в ост. случаях |
(3) |
|
||||||
|
|
|
|||||||||
|
|
x + 2 , |
если x ≥ 7 или x = −1 |
( |
|||||||
y = |
|
−1 , |
если 0 < x < 7 |
|
( |
||||||
x |
|
||||||||||
|
|
|
x2 |
+ 4 |
|
в ост. случаях |
|
(3 |
|||
|
|
|
|
||||||||
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
lg2 x +1, |
если x ≥1 |
(1) |
|
||||||
y = |
|
|
|
|
|
|
если x ≤ −1 |
(2) |
|
||
1/ x +ex , |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
2 |
|
в ост. случаях |
(3) |
|
||
|
0,5x |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
||
179
Лабораторная работа №11 AutoLISP. Попадание точки в область – 1
Цель работы. Дальнейшее изучения языка AutoLISP. Управление средой AutoCAD. Определение попадания точки в область, заданную рисунком.
Постановка задачи
1.Запрограммировать отображение заданной области на экране. Вариант задания находится в таблице 11.1.
2.Организовать ввод данных о точке в программу.
3.Осуществить проверку попадания точки в заданную область.
4.Показать введенную пользователем точку на экране и ее координаты
5.Вывести сообщение о попадании или не попадании точки в область.
6.Предложить повторить действия с пункта 2.
Требования к отчету
Отчет должен содержать титульный лист с названием лабораторной работы
1.Цель работы.
2.Краткие теоретические сведения.
3.Листинг программы.
4.Результаты работы программы.
Индивидуальные варианты задания находятся в табл. 11.1
Вопросы для защиты
1.Функции условного ветвления программы.
2.Функции цикла.
3.Арифметические функции.
4.Функции присваивания. Создание подпрограмм, запуск подпрограмм.
5.Управление средой AutoCAD.
Некоторые кирпичики для вашей программы
1. Изменение текущего рабочего цвета.
(command "_.color" "цвет")
180
