
154эл
.pdf
В данном случае х>0 соответствует сжатию пружины, а х<0 – растяжению пружины.
Итак,
x x0 |
x02 2x0h v2 |
x0 8 10 2 |
м. |
|
g |
|
|
Пример 4. Стержень массой m = 6 кг и длиной l = 2 м может вращаться в вертикальной плоскости относительно горизонтальной оси, проходящей через точку О (рис. 1.4). В конец стержня попадает
пуля массой m0 = 10 г, летевшая со скоростью v0 = 1·103 мс ,
направленной перпендикулярно стержню и оси, и застревает в нем. Определить кинетическую энергию стержня после удара.
Решение. Система состоит из двух тел: стержня и пули. Для решения применим законы сохранения.
По закону сохранения момента импульса m0v0l J ,
где m0v0l - момент импульса пули относительно оси вращения до удара,
J - момент импульса стержня и пули относительно оси вращения после удара.
m0Jv0l .
Момент инерции стержня
21

|
|
O |
|
|
|
|
|
|
|
|
|
Jcm |
1 ml2 . |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
v0 |
|
|
|
|
|
|
|
|
|
|
|
Момент инерции пули |
||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
J |
|
m l 2 . |
|
|
m0 |
|
|
|
|
|
|
|
|
|
|
п |
|
||
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
m |
|
|
|
0 |
|
|||||
|
|
|
|
|
|
|
т.к. m m0 , то |
|||||||
|
|
Рис. 1.4. |
|
|
||||||||||
Jn Jcm , то J Jcm |
|
1 ml 2 . |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
Кинетическая энергия стержня |
|
|||||||||||||
|
|
J 2 |
|
|
m2v2l2 |
|
3m2v2 |
|
|
|||||
Eк |
|
|
|
|
0 0 |
|
|
|
0 0 . |
|
||||
2 |
|
|
|
|||||||||||
|
|
|
|
|
|
2J |
|
|
2m |
|
|
|
||
Eк 25 Дж.
Заметим, что начальная кинетическая энергия пули до удара
E0 m02v0 5 103 Дж, что значительно больше кинетической энергии
системы после удара, т.е. в результате неупругого удара большая часть начальной механической энергии превратилась в немеханические виды энергии.
Пример 5. Материальная точка участвует одновременно в двух
колебаниях |
вдоль |
оси |
ОХ: |
x1 |
|
a |
|
2 t |
|
|
и |
|||||||
2 |
3 cos |
6 |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
x2 |
|
a |
|
2 t |
|
|
, а |
также |
вдоль |
оси |
ОY: |
y bcos t . |
Найти |
|||||
2 |
cos |
3 |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
траекторию результирующего колебания.
Решение. Сложим сначала колебания происходящие вдоль оси
ОХ
x x1 x2 , x Acos 2 t .
22
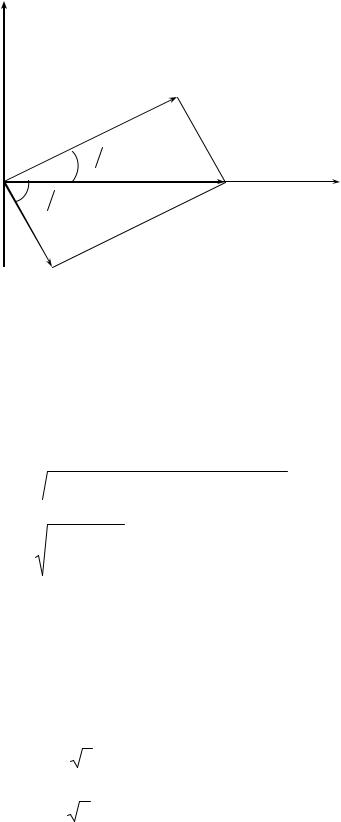
Y |
|
|
|
|
|
Для |
наглядности |
||
|
|
|
|
|
|
воспользуемся |
|||
|
|
|
|
|
графическим |
методом |
|||
|
|
|
A1 |
|
сложения |
колебаний. |
|||
|
|
|
|
Каждому |
колебанию х1 |
||||
|
|
|
|
|
и |
х2 |
поставим |
в |
|
|
|
6 |
A |
|
соответствие векторы A1 |
||||
0 |
|
|
|
X |
и A2 , длины |
которых |
|||
3 |
|
|
|
|
равны |
амплитудам |
|||
|
|
|
|
|
|
соответствующих |
|||
|
|
|
|
колебаний, |
а |
углы |
|||
A2 |
|
|
|
|
наклона к оси ОХ -– |
||||
|
|
|
|
|
|||||
|
Рис. 1.5. |
|
|
начальным фазам (рис. |
|||||
|
|
|
|
|
1.5). |
|
|
|
|
Тогда |
результирующему |
колебанию |
ставится в |
соответствие |
|||||
вектор |
|
|
|
|
|
|
|
|
|
A . |
|
|
|
|
|
|
|
|
|
Амплитуду результирующего колебания найдем по формулам:
A 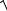 A12 A22 2A1 A2 cos 2 1 ,
A12 A22 2A1 A2 cos 2 1 ,
A |
3a2 |
|
a2 |
a . |
|
|
|
|
|
|
|
|
||||
4 |
4 |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Тангенс начальной фазы результирующего колебания |
|||||||||||||||
определим по формулам: |
|
|
|
|
||||||||||||
tg |
|
A1 sin 1 |
A2 sin 2 |
|
, |
|
|
|||||||||
|
|
|
|
|
||||||||||||
|
|
A cos |
1 |
A |
|
cos |
2 |
|
|
|
|
|
||||
|
1 |
|
|
|
2 |
|
|
|
|
|
|
|
||||
|
|
a |
3 sin |
|
|
a |
|
|
|
|
|
|
||||
|
|
2 |
6 |
2 |
sin |
|
3 |
|
|
|||||||
tg |
|
|
|
|
|
|
|
|
|
|
0. |
|||||
|
a |
3 cos |
|
|
a |
|
|
|
|
|||||||
|
|
|
|
|||||||||||||
|
2 |
6 |
2 |
cos |
3 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
||||||||
23

Итак, результирующее колебание вдоль оси ОХ
x a cos 2 t
складываем с колебанием вдоль оси ОY y bcos t .
Чтобы найти траекторию результирующего колебания исключим время.
Уравнение x a cos 2 t представим в виде:
x a 2cos2 t 1 ,
cos t |
y |
. |
|
|
|
|
|
|
|
|
|
|
|
||
|
b |
|
|
|
|
|
|
|
|
|
|
2 y2 |
|
|
|
Тогда |
|
|
|
|
- траектория представляет собой параболу |
||
|
2 |
||||||
x a |
b |
1 |
|||||
|
|
|
|
|
|
|
|
(рис. 1.6).
Y
b
 2
2
0 |
X |
|
-a |
||
|
b2
Рис. 1.6.
24
2. Основы молекулярной физики и термодинамики
2.1. Молекулярно-кинетическая теория
Основное уравнение молекулярно-кинетической теории связывает параметры состояния газа с характеристиками движения его молекул, т.е. устанавливает зависимость между давлением, объемом газа и кинетической энергией поступательного движения его молекул:
p 13 n m0 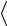 vкв
vкв 2 , (42) p n k T , (43)
2 , (42) p n k T , (43)
p 23 n 
 , (44)
, (44)
где  vкв
vкв - средняя квадратичная скорость молекул;
- средняя квадратичная скорость молекул;
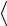
 - средняя кинетическая энергия поступательного движения молекул;
- средняя кинетическая энергия поступательного движения молекул;
n VN - концентрация молекул;
m - масса молекулы газа, m |
|
|
; |
|
|
||||
0 |
0 |
|
N A |
|
|
|
|
||
k 1,38 10 23 ДжК - постоянная Больцмана;
V - объем газа;
Nm N A - число молекул газа;
- молярная масса;
25

m - масса газа;
N A 6,02 1023 моль-1 – постоянная Авогадро; v m - количество вещества (число молей).
Средняя кинетическая энергия поступательного движения молекулы
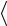
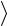 32 kT . (45)
32 kT . (45)
Средняя энергия молекул
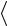
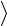 2i kT , (46)
2i kT , (46)
где i - число степеней свободы; i 3 - одноатомный газ;
i5 - двухатомный газ;
i6 - многоатомный газ; Сравнивая значения
|
|
|
|
|
m |
v2 |
|
|
|
|
3 kT |
|
|
|||
|
|
|
|
|
|
0 |
кв |
|
|
и |
|
получим: |
||||
|
|
|
|
|
2 |
|
|
|||||||||
|
|
|
v2 |
|
|
|
|
|
|
2 |
|
|
||||
|
m |
|
|
|
3 |
|
|
|
|
|
|
|
||||
0 |
|
|
кв |
|
|
kT |
откуда: |
|
|
|
||||||
|
|
2 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
||
|
vкв |
|
|
3kT |
3RT |
, (47) |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
m0 |
|
|
|
|
|
|
|
где |
|
|
vкв |
- средняя квадратичная скорость молекул; |
||||||||||||
|
|
|
k |
|
|
R ; |
|
R k N A ; R 8,31 |
Дж |
- универсальная газовая |
||||||
|
|
|
m0 |
|
моль К |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
постоянная.
|
Средняя арифметическая скорость молекул |
||
v |
8kT |
8RT |
. (48) |
|
m |
|
|
|
0 |
|
|
|
Наиболее вероятная скорость молекул |
||
vв |
2kT |
2RT |
. (49) |
|
m0 |
|
|
26
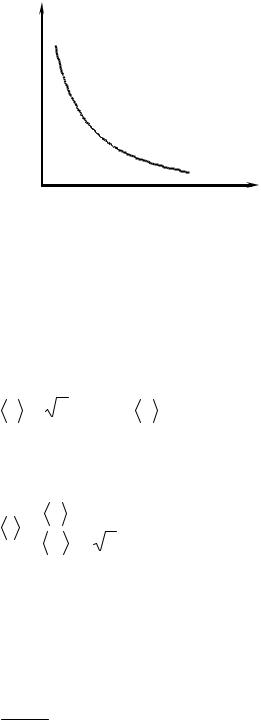
Распределение Больцмана для молекул во внешнем потенциальном поле (в поле силы тяжести). График приведен на рис. 2.1
|
|
|
|
|
|
|
|
|
n n0 e |
m0 g h |
n0 e |
g h |
, (50) |
||
n |
|
|
|
|
|
|
|
|
|
k T |
|
R T |
|||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
где n и n0 соответственно |
||||||
|
|
|
|
|
|
|
|
|
концентрация молекул на высоте h |
||||||
|
|
|
|
|
|
|
|
|
и h0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Выражение |
|
для |
||||
|
|
|
|
|
|
|
|
|
распределения |
Больцмана можно |
|||||
|
|
|
|
|
|
|
|
|
преобразовать в барометрическую |
||||||
|
|
|
|
|
|
|
|
h |
формулу, используя |
соотношение |
|||||
|
|
|
|
|
|
|
|
p nkT : |
|
|
|
|
|
||
|
|
|
|
Рис. 2.1. |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
p p0 e |
|
m0 g h |
p0 |
e |
g h |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
||||||||
|
|
k T |
R T , (51) |
|
|
|
|
|
|
|
|||||
где p и p0 |
соответственно давление газа на высоте h и h0 . |
|
|||||||||||||
|
Среднее число соударений испытываемых одной молекулой в |
||||||||||||||
единицу времени: |
|
|
|
|
|
|
|
|
|
||||||
z |
2 d 2n v , (52) |
|
|
|
|
|
|
|
|||||||
где d - эффективный диаметр молекулы; |
|
|
|
|
|
|
|||||||||
d 2 - эффективное сечение молекулы. |
|
|
|
|
|
|
|||||||||
|
Средняя длина свободного пробега молекулы газа: |
|
|
||||||||||||
l |
v |
|
|
|
1 |
|
. (53) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Z |
2 d 2 |
n |
|
|
|
|
|
|
|
||||||
|
Уравнения состояния идеального газа: |
|
|
|
|
|
|||||||||
для одного моля газа - |
p V R T , (54) |
|
|
|
|
|
|
||||||||
для произвольного числа молей газа - p V v R T , |
|
|
|||||||||||||
где v m - число молей.
p V const , (55) T
где V - объем одного моля.
Изотермический процесс (T const , m const ) p1 V1 p2 V2 или p V const . (56)
27

Изобарный процесс ( p const , m const )
V1 |
V2 |
или |
V |
const . (57) |
T |
T |
|
T |
|
1 |
2 |
|
|
|
Изохорный процесс (V const , m const )
p1 |
|
p2 |
или |
p |
const . |
|
T |
T |
T |
||||
|
|
|
||||
1 |
|
2 |
|
|
|
(58)
Для смеси идеальных газов справедлив закон Дальтона
n
p pi , (59)
i 1
где pi - парциальное
давление i-го компонента смеси, т.е. давление, которое производил бы газ, если бы только он один находился в сосуде занятой смесью.
2.2. Основы термодинамики
Первое начало термодинамики: количество теплоты, сообщаемое системе Q , расходуется на изменение внутренней
энергии dU и на совершение системой работы A против внешних сил:
Q dU A, (60)
где Q - элементарное количество теплоты;
A - элементарная работа;
dU - бесконечно малое изменение внутренней энергии. Внутренняя энергия произвольной массы газа:
Um i RT . (61)
2
Изменение внутренней энергии идеального газа:
dU m i RdT . (62)
2
28

Работа при изменении объема газа:
V2
A pdV , (63)
V1
где V1 и V2 начальный и конечный объем газа.
Работа газа:
при изобарном процессе ( p const )
A p V2 V1 m R T2 T1 , (64)
при изотермическом процессе (T const )
A |
m |
RT ln V2 |
|
m |
RT ln |
p1 |
|
, (65) |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
V |
|
|
|
|
|
p |
2 |
|
|
|
|
|
|
|
||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
при адиабатном процессе ( Q 0 ) |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
m i |
|
|
|
|
RT1 |
|
m |
|
|
|
|
|||||||
A |
R T1 T2 |
|
|
|
V1 |
|
|
|
|||||||||||
|
|
|
|
|
|
|
1 V |
|
|
|
, (66) |
||||||||
|
2 |
1 |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
где T1 , T2 и V1, V2 - соответственно начальная и конечная
температуры и объемы газа.
Процесс, протекающий без теплообмена с внешней средой ( Q 0) называется адиабатным.
pV
где
Уравнение адиабатного процесса:
const , |
TV 1 const , |
T p1 const , (67) |
C
p - показатель адиабаты.
CV
График адиабатного процесса рис. 2.3. p
Изотерма
Адиабата
 V
V
Рис. 2.3.
29

Количество теплоты при малом изменении температуры:
Q cmdT , (68)
где c - удельная теплоемкость. Теплоемкость массы газа:
C m dQT .
Удельная теплоемкость: c mdQT .
Связь между молярной C и удельной теплоемкостями газа:
C c .
Молярные теплоемкости газа при постоянном объеме и постоянном давлении:
CV 2i R , Cp i 2 2 R . (69)
Уравнение Майера:
Cp CV R i 2 2 R . (70)
Количество теплоты сообщаемое термодинамической системе в изопроцессах:
при изохорном процессе ( A 0 ): dQ m CV dT ; (71)
при изобарном процессе: dQ m CV dT m RdT . (72)
Термический коэффициент полезного действия для кругового процесса (цикла):
|
A |
|
Q1 Q2 |
1 |
Q1 |
, (73) |
|
Q |
|||||||
|
|
Q |
|
Q |
|
||
|
1 |
|
1 |
|
2 |
|
где Q1 - количество теплоты, полученное системой от нагревателя; Q2 - количество теплоты, отданное системой холодильнику;
A - полезная работа совершаемая за цикл.
Термический коэффициент полезного действия цикла Карно:
T1 T2 1 T2 , (74)
T1 T1
30
