Лекции / семестр4 / Лекции МП-2 (Альшина) / Pr1

§24. Изолированные особые точки однозначной аналитической функции. Особые точки.

Определение. Точка z₀ называется изолированной особой точкой функции f(z), если f(z) однозначная и f(z)C^(0<|z-z₀|<(z₀)), а точка z₀ является особой точкой функции f(z).

Другими словами, точка z₀ называется изолированной особой точкой функции f(z), если такая окрестность точки z₀ , в которой нет других особых точек функции f(z). В самой особой точке z₀ функция f(z) может быть не определена. Функцию f(z) в окрестности точки z₀ можно разложить в ряд Лорана, сходящийся в кольце 0<|z-z₀|<(z₀). Поведение функции f(z) в окрестности точки z₀ определяется главной частью ряда Лорана, т.к. регулярная часть ряда Лорана, очевидно, является непрерывной в окрестности точки z₀ и равна c₀ в ней.

1. Классификация изолированных особых точек

Возможны три случая:

Название особой точки		Коэффициенты ряда Лорана	Главная часть ряда Лорана
Устранимая особая точка	 конечный предел	,  n>0	отсутствует
Полюс порядка m	, но 	,  n>m	Содержит не более m членов
Существенно особая точка	не существует	 N>0  n>N:	Содержит бесконечно много членов

Проиллюстрируем их:

1) Определение. Если главная часть ряда Лорана с центром разложения в особой точке равна 0, то называется устранимой особой точкой.

Для n>0 c_-n=0  главная часть ряда Лорана =0;

Тогда .

Если функция не определена в точке z₀ , то ее можно доопределить по непрерывности, положив f(z₀)=c₀ .

Теорема 24.1 Если f(z)C^(0<|z-z₀|<(z₀)) и |f(z)|<M при 0<|z-z₀|<(z₀), то z₀ - устранимая особая точка.

Функция ограничена по модулю в окрестности устранимой особой точки.

Доказательство. Разложим f(z) в ряд Лорана и рассмотрим выражение для коэффициентов главной части.

, n>0

В качестве контура интегрирования выберем круг с центром в точке z₀ и радиуса 

С_: |-z₀|=. Тогда, сделав замену -z₀= e^i, d=ie^idи учтя, что |e^in|=1, получим оценку: |c_-n|< M^n-10 при 0. Т.к. значения c_-n не зависят от , то c_-n=0. 

Замечание. В окрестности устранимой особой точки верно представление , где и .

2) Определение. Если главная часть ряда Лорана функции f(z) в окрестности ее изолированной особой точки z₀ содержит конечное число членов:

для причем

то z₀ - называется полюсом порядка m.

В окрестности полюса верно представление

;

 и (z₀)0.

Из такого представления функции f(z) вблизи полюса порядка m видно, что f(z) неограниченно возрастает при zz₀. Верна и обратная теорема.

Теорема 24.2 Если f(z)C^(0<|z-z₀|<(z₀)), z₀ - изолированная особая точка f(z) и (независимо от способа стремления z к z₀ ), то z₀ - полюс f(z).

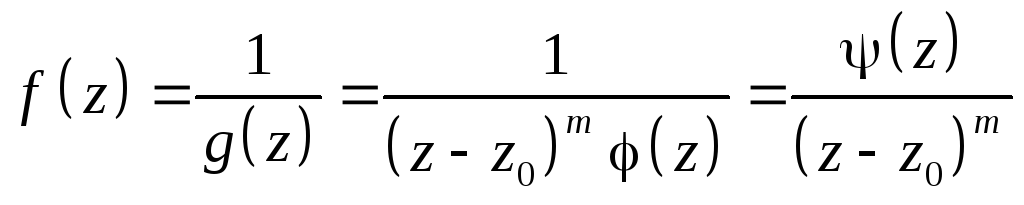Доказательство. => для A>0 : 0<|z-z₀|< , |f(z)|>A; Рассмотрим g(z)=1/f(z); g(z)C^(0<|z-z₀|<); |g(z)|<1/A=M => z₀ – нуль для функции g(z)  g(z)=(z-z₀)^m(z), m>0 , (z₀)0  , и (z₀)0 

Замечание. Точка z₀, являющаяся нулем порядка m для функции g(z), является полюсом того же порядка для функции f(z)=1/g(z)!

3) Определение. Точка z₀ называется существенно особой точкой функции f(z), если главная часть ряда Лорана функции f(z) в окрестности ее изолированной особой точки z₀ содержит бесконечно много членов.

Бесконечное число коэффициентов c_-n0.

Поведение аналитической функции в окрестности существенно особой точки описывается следующей теоремой.

Теорема Сохоцкого-Вейерштрасса Для комплексного числа B и >0, в  -окрестности существенно особой точки z₀ z₁: |z₁-z₀|< и |f(z₁)-B|<.

Доказательство . (От противного)

Пусть такие ₀ и ₀: для z 0<|z-z₀|<₀; |f(z)-B|>₀. Рассмотрим g(z)=1/[f(z)-B]. В указанной окрестности |g(z)|=1/|f(z)-B|<1/₀=M  g(z) – ограниченна по модулю. Т.о. z₀ - устранимая особая точка g(z) (по Теореме 24.1)  g(z)=(z-z₀)^m(z), m0 , (z₀)0. Т.о. f(z)=B+1/[(z-z₀)^m(z)]=B+(z-z₀)^-m(z); (z₀)0  z₀- либо полюс f(z) m>0, либо устранимая точка при m=0. Получили противоречие. 

 Замечание 1. {_n}0 =>{z⁽ⁿ⁾₁}z₀. {f(z⁽ⁿ⁾₁)}B  в окрестности существенно особой точки можно выбрать {z⁽ⁿ⁾₁}z₀ такую, что {f(z⁽ⁿ⁾₁)} сходится к наперед заданному числу B.

Пример . f(z)=e^1/z точка z=0 - существенно особая.

Важное замечание В окрестности точки ветвления и неизолированной особой точки вообще нельзя раскладывать в ряд Лорана!

2. Еще раз о бесконечно удаленной точке.

Определение. Точка z= является изолированной особой точкой функции f(z) если  R>0: f(z) не имеет особых точек при R<|z|<.

Т.к. f(z)C^( R<|z|<), то при R<|z|<.

Возможны три случая:

Название особой точки		Коэффициенты ряда Лорана	Главная часть ряда Лорана
Устранимая особая точка	 конечный предел	,  n>0	отсутствует
Полюс порядка m	, но 	,  n>m	Содержит не более m членов
Существенно особая точка	не существует	 N>0  n>N:	Содержит бесконечно много членов

Полезно помнить, что преобразование переводит точку в , характер же особой точки при таком преобразовании не меняется.

Примеры: Классифицировать особые точки, включая z=

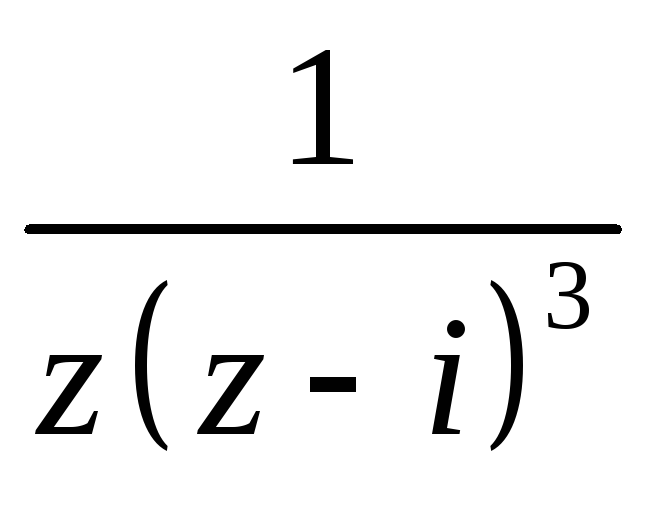1. z=0 полюс 1-го порядка, z=i - полюс третьего порядка, z= устранимая особая точка.

2. z=0 существенно особая точка, z= устранимая особая точка.

3. z_k=k полюса 1-го порядка, z= точка сгущения полюсов – неизолированная особая точка.

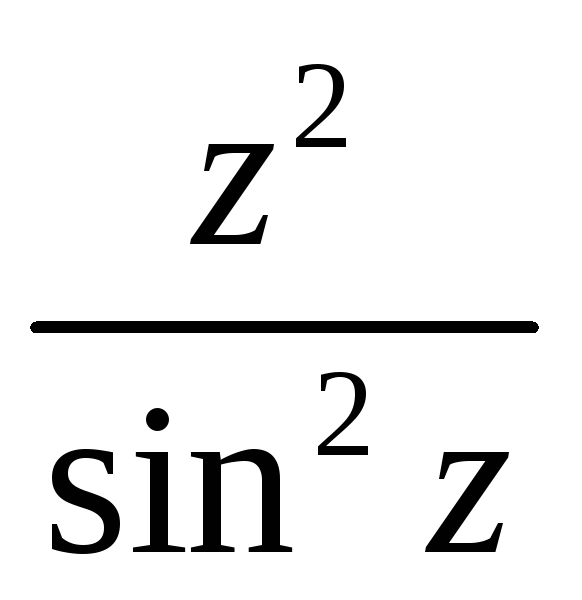4. z_k=k полюса 2-го порядка k0, z=0 – устранимая особая точка, z= точка сгущения полюсов – неизолированная особая точка.