
Лекция 1
.pdf
Проф. Власов А.Н. Материалы лекций по курсу «ОБЩАЯ ФИЗИКА» 2013/2014 |
21 |
|
1-й семестр. Лекция № 1 |
||
|
||
|
|
|
|
|
|
|
|
b |
cos |
||
a,b |
a |
|||
где — угол между векторами.
(1.4)
В координатной форме скалярное произведение равно сумме парных произведений одноименных координат векторов:
|
|
a b |
a,b |
||
|
|
x x |
ayby
azbz
.
(1.5)
Проекцией вектора |
|
a |
вектор которой равен произведение
a |
l |
|
|
|
на некоторую ось, единичный
|
|
|
|
|
l |
, называется |
скалярное |
|
|
. |
|
a,l |
(1.6) |
||
На рис. 1.4 изображены два случая: первый, когда проекция вектора положительна, и второй, когда она отрицательна (угол — тупой).
21
Проф. Власов А.Н. Материалы лекций по курсу «ОБЩАЯ ФИЗИКА» 2013/2014 |
22 |
|
1-й семестр. Лекция № 1 |
||
|
||
|
|
Скалярное произведение — коммутативно, т. Е. его величина не зависит от порядка сомножителей.
|
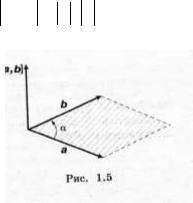
Векторным произведением |
|
|
|
двух векторов |
|
и |
||||
|
a, b |
a |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
b |
называется вектор, |
модуль которого равен, (рис. 1.5). |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b sin |
|
|
|
|
||||
|
a,b |
a |
. |
(1.7) |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
перпендикулярен плоскости, в которой |
|||||||||
Вектор a,b |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
лежат |
a |
и |
, а его направление определяется |
по |
|||||||||
|
|
||||||||||||
следующему |
правилу: если |
смотреть с |
конца |
вектора |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
векторного |
|
произведения |
на векторы |
a |
и |
|
, |
то |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
кратчайший поворот от вектора |
a |
к вектору |
будет |
||||||||||
|
|
||||||||||||
происходить против часовой стрелки.
Отметим, что такая тройка векторов называется
правой.
Модуль векторного произведения равен площади
параллелограмма, |
построенного |
на |
векторах- |
сомножителях. |
|
|
|
22

Проф. Власов А.Н. Материалы лекций по курсу «ОБЩАЯ ФИЗИКА» 2013/2014 |
23 |
|
1-й семестр. Лекция № 1 |
||
|
||
|
|
Векторное произведение – некоммутативно, оно меняет знак при перестановке сомножителей.
Векторное |
|
произведение |
при |
координатном |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
представлении векторов a |
|
и b : |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
e |
x |
e |
y |
e |
z |
|
|
|||
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
a, b |
|
ax |
|
ay |
az |
|
(1.8) |
||||||
|
|
|
|
b |
x |
|
b |
y |
b |
z |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|||
c
Двойное векторное произведение трех векторов , определяется по формуле:
a ,
b
и
|
|
|
|
a, b,c |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b a,c |
c a,b |
|||
.
(1.9)
|
|
|
|
|
|
|
Смешанное произведение трех векторов |
, |
b |
и |
|||
a |
c |
может быть найдено, если воспользоваться правилами для векторного произведения, которое выполняется в первую
очередь, |
и скалярного произведения, выполняемого |
во |
|||
вторую |
очередь. Смешанное произведение |
|
|
|
|
a, b,c |
|||||
численно равно объему параллелепипеда, построенного на |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
||
векторах |
a |
, |
и |
c |
. |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
ax |
ay |
az |
|
|
|
|
|
|
|
by |
bz |
|
|
|
|
|
|
a, b, c bx |
||||
|
|
|
|
|
|
|
cx |
cy |
cz |
23

Проф. Власов А.Н. Материалы лекций по курсу «ОБЩАЯ ФИЗИКА» 2013/2014 |
24 |
|
1-й семестр. Лекция № 1 |
||
|
||
|
|
8. Элементы математического анализа
Производная. |
||
Если |
f x |
— непрерывная функция |
|
||
переменной, |
то ее производной называется |
|
одной
f |
|
|
df |
lim |
f x x f x |
|
x |
dx |
x |
||||
|
|
x 0 |
||||
|
|
|
Частная производная.
.
Рассмотрим |
|
непрерывную функцию |
|
нескольких |
||||||
переменных |
— |
|
f x, y,z . |
Частной производной |
этой |
|||||
функции по |
|
одной из |
переменных, например, |
по |
||||||
переменной |
|
x |
называется: |
|
|
|
|
|
||
|
|
|
|
|
|
|
||||
f |
lim |
f x x, y,z f x, y,z |
|
|
|
|
||||
x |
|
x |
|
|
|
|
||||
|
x 0 |
. |
|
(1.10) |
||||||
|
|
|
|
|
|
|
|
|||
При вычислении частной производной по |
|
x |
согласно |
|||||||
|
|
|||||||||
(1.10) приращение испытывает лишь аргумент х, в то время как у, z остаются фиксированными. Частные производные по другим переменным вычисляются аналогично.
Итак, чтобы найти частную производную по какомулибо аргументу, нужно продифференцировать функцию
24

Проф. Власов А.Н. Материалы лекций по курсу «ОБЩАЯ ФИЗИКА» 2013/2014 |
25 |
|||||
|
1-й семестр. Лекция № 1 |
|
||||
|
|
|
||||
|
|
|
||||
f x, y,z |
по этому аргументу, считая при |
этом все |
||||
остальные аргументы фиксированными. |
|
|
||||
Полная производная сложной функции. |
|
|||||
Рассмотрим функцию |
f x, y,z,t , где |
x x t , |
||||
y y t , |
z z t , |
t |
— имеет смысл |
параметра |
||
(например, функции образом:
времени). Тогда
по параметру |
t |
полная производная этой вычисляется следующим
df |
|
f |
|
f |
|
dx |
|
f |
|
dy |
|
f |
|
dz |
|
|
dt |
t |
x |
dt |
y |
dt |
z |
dt |
|
|
|||||||
|
|
|
|
|
|
|
. |
(1.11) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Неопределенный интеграл. |
|
|
||
Если |
F x и |
f x непрерывны |
в некотором |
|
|
|
|
|
F x |
промежутке, причем производная F x f x , то |
|
|||
называется первообразной для f x в этом промежутке.
Множество всех первообразных F x C называется неопределенным интегралом:
f x dx F x C
где С — произвольная постоянная.
,
(1.12)
25

Проф. Власов А.Н. Материалы лекций по курсу «ОБЩАЯ ФИЗИКА» 2013/2014 |
26 |
|
1-й семестр. Лекция № 1 |
||
|
||
|
|
Определенный интеграл.
Понятие определенного интеграла введем на примере
вычисления площади криволинейной трапеции (рис. 1.6), |
||||||||||
т. Е. фигуры, ограниченной графиком функции |
y f x |
, |
||||||||
|
|
|
||||||||
осью |
x |
и прямыми, перпендикулярными |
оси |
x |
и |
|||||
|
|
|||||||||
проходящими через точки |
a |
и |
b |
. |
|
|
|
|
||
|
|
|
|
|
|
|||||
Разобьем отрезок |
a;b на бесконечно малые элементы |
||||||
длиной |
x |
1,2, ... N |
и обозначим некоторое |
среднее |
|||
i |
|
|
|||||
|
|
|
|
|
|
|
|
значение координаты i |
-го элемента |
~ |
|
|
|||
x . |
|
|
|||||
|
|
|
|
|
i |
|
|
На каждом элементе |
~ |
построим прямоугольник высотой |
|||||
x |
|||||||
|
|
|
i |
|
|
|
x . |
~ |
|
площадь |
|
которого |
|
~ |
|
f x , |
|
|
S f x |
||||
i |
|
|
|
|
i |
i |
i |
Просуммировав площади всех таких прямоугольников, мы приближенно найдем общую площадь криволинейной трапеции
|
|
i |
i |
S |
|
~ |
x . |
|
f x |
Очевидно, что точность вычисления площади будет тем выше, чем меньше длина каждого элемента xi , т. Е.
26
Проф. Власов А.Н. Материалы лекций по курсу «ОБЩАЯ ФИЗИКА» 2013/2014 |
27 |
|
1-й семестр. Лекция № 1 |
||
|
||
|
|
«мельче»
N )
разбиение отрезка a;b . В пределе ( получим точный результат:
x 0
и
|
N |
i |
i |
|
|
||
S lim |
|
~ |
x |
|
f x |
||
x 0 |
i 1 |
|
|
|
|
|
b
a
f
x dx
.
Этот предел в математике называется определенным интегралом. С геометрической точки зрения определен-
ный интеграл представляет собой площадь криволинейной трапеции. В механике с помощью определенного интеграла можно вычислять массу тела, момент инерции и другие величины.
Вычисление определенного интеграла производится по формуле Ньютона—Лейбница:
b
a
f x dx
F b
F
a
,
где
F x
— первообразная
f x
на отрезке
a;b
.
27
Проф. Власов А.Н. Материалы лекций по курсу «ОБЩАЯ ФИЗИКА» 2013/2014 |
28 |
|
1-й семестр. Лекция № 1 |
||
|
||
|
|
10.Литература
1.Детлаф А.А., Яворский Б.М. Курс физики: учеб пособие для втузов. – М.: Изд. Центр «Академия»,
2007. – 720 с.
2.Курс физики: Учебник для вузов: В 2 т. Т. 1 / Под ред. В.Н. Лозовского. – СПб.: Изд-во «Лань», 2003.
–576 с..
3.Яворский Б.М. Справочник по физике. М.: ООО
«Издательство Оникс», 2008. – 1056 с.
4.Бондарев Б.В. Курс общей физики. КН. 1.Механика.
–М.: Высш. Шк., 2005. – 352 с.
5.Савельев И.В. Курс общей физики: Т. 1. Механика.
–Изд-во «Лань», 2007. 432 с.
6.Валишев М.Г., Повзнер А.А. Курс общей физики: Учебное пособие. – СПб.: «Лань», 2009. – 476 с.
7.Курс физики / Г.А. Бордовский и др. – М.: Высш.
Шк., 2004. – 423 с.
_ _ _ _ _
28
