Решение.

1. Для доказательства того, что система векторов является базисом в пространстве , достаточно найти определитель матрицы, составленной из компонент этих векторов:

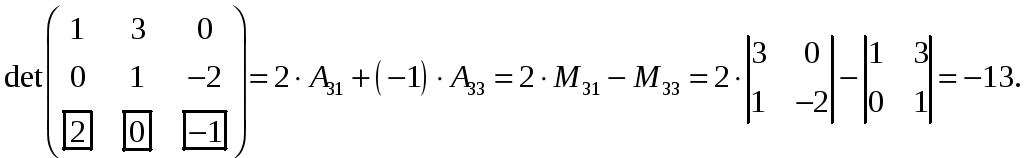
Так как определитель матрицы отличен от нуля, то система векторов является базисом в пространстве .

2. Напишем формулы преобразования координат при переходе от стандартного базиса :

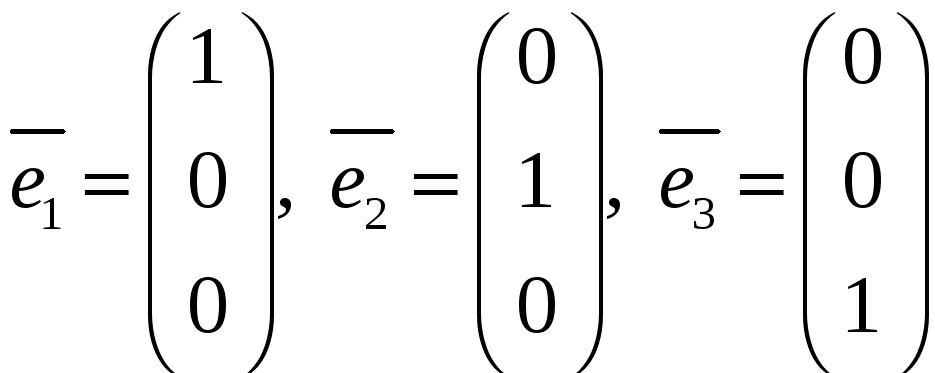
к базису .

Разложим векторы по векторам . Например, вектор раскладывается следующим образом:

.

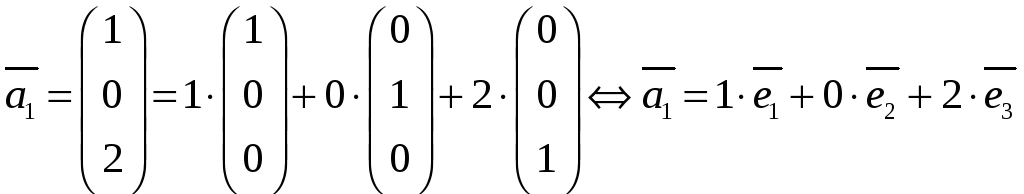Аналогично можно поступить и с остальными векторами. В результате получаем следующую систему

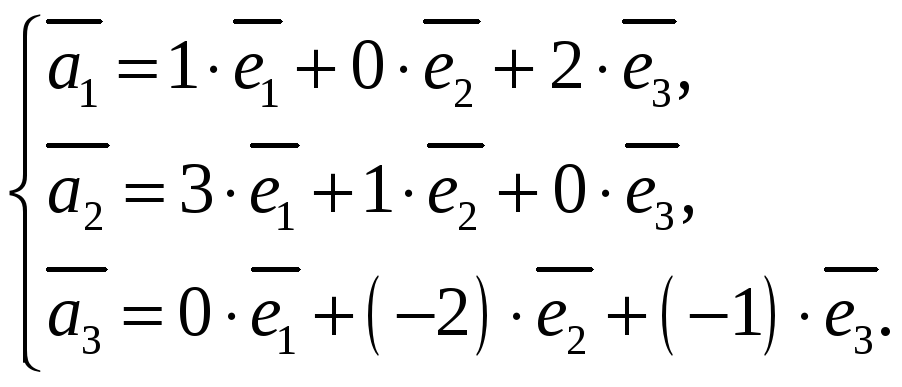
Составляем матрицу

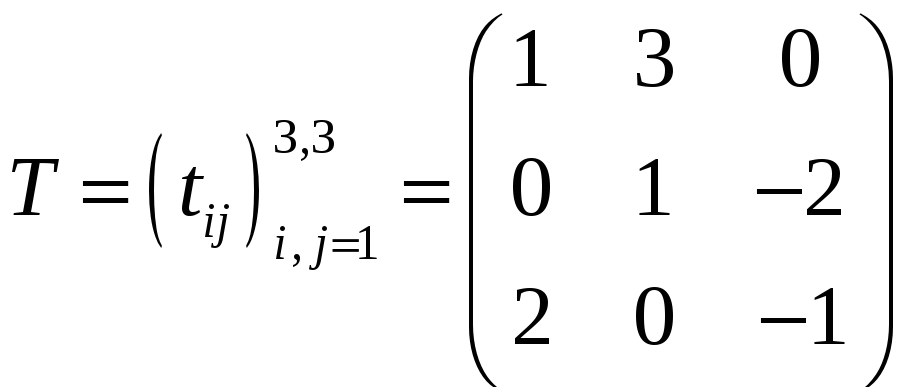
перехода от стандартного базиса к базису (ее столбцами являются компоненты вектор-столбцов , которые являются координатами этих векторов в стандартном базисе).

Теперь составим формулы преобразования координат при переходе от базиса к базису. Пусть вектор в базисе имеет следующий координатный вектор-столбец

,

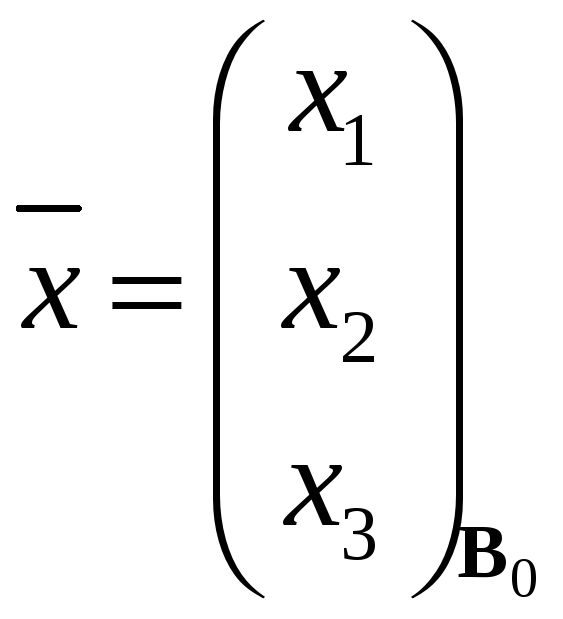а в базисе координатный вектор-столбец

.

Тогда имеет место формула

, (5)

где матрица, обратная к матрице перехода.

Найдем обратную матрицу по формуле

,

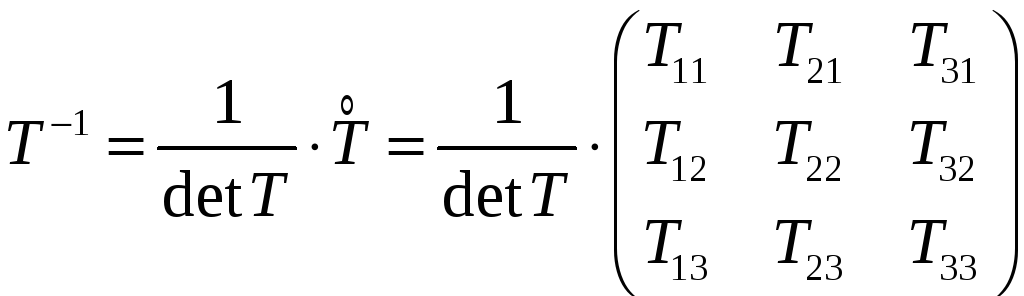где алгебраическое дополнение для элемента матрицы перехода (при этом ).

Для удобства вычислений составим таблицу алгебраических дополнений:

В результате обратная матрица к матрице перехода примет вид

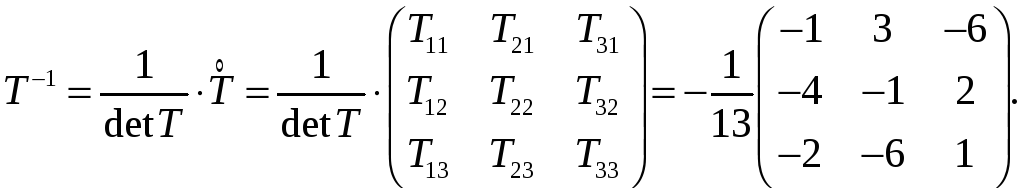
При этом формула (5) примет вид

.

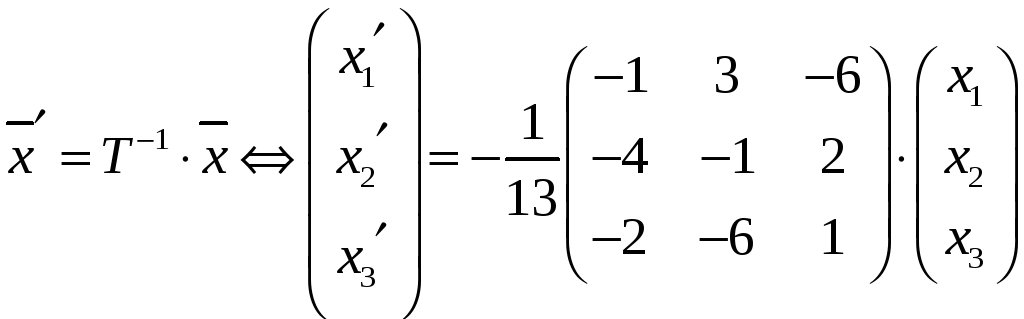Расписывая покоординатно последнее матричное равенство, получим систему, описывающую связь координат вектора в новом базисе с координатами вектора в старом базисе :

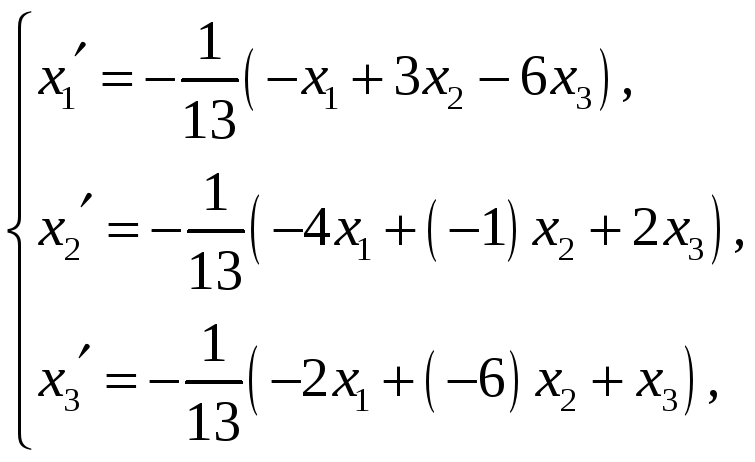
или

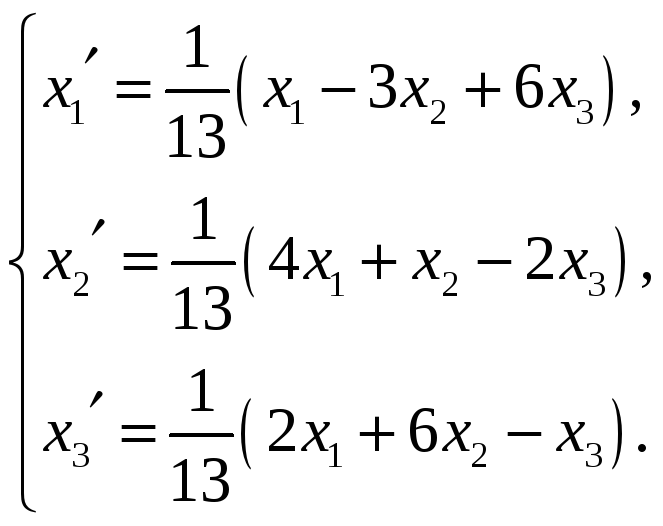(6)

Итак, формулы преобразования координат при переходе от базиса к базису имеют вид (6). Теперь если вектор имеет в базисе координатный вектор-столбец

,

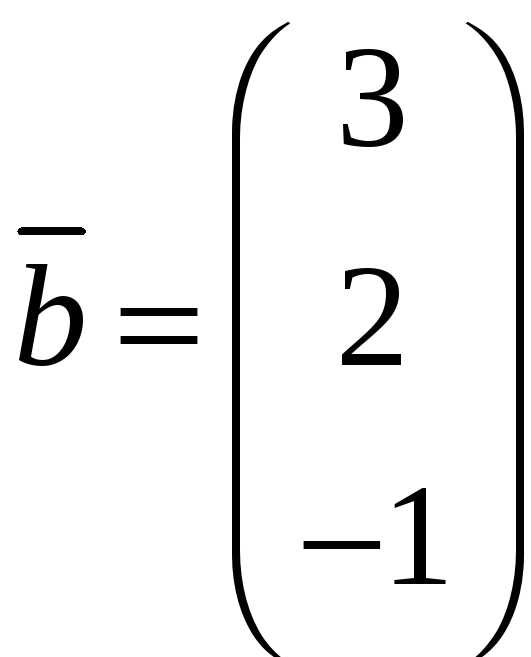то пользуясь формулами (6), найдем координатный вектор-столбец вектора в базисе (подставляем в формулы (6) )

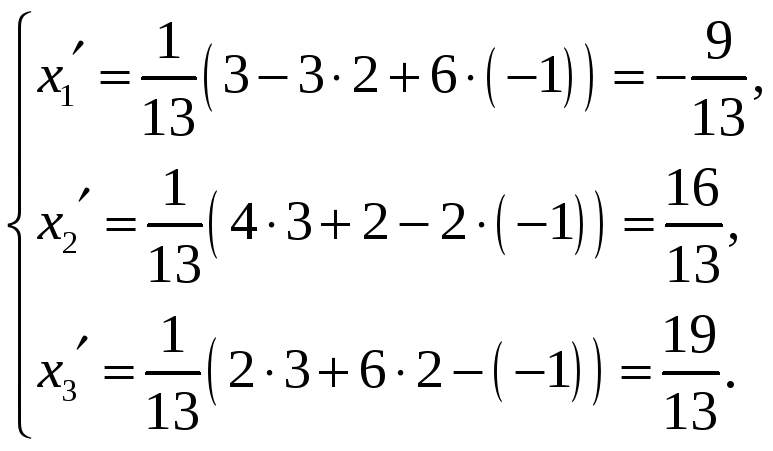
Пример 5. Даны векторы

.

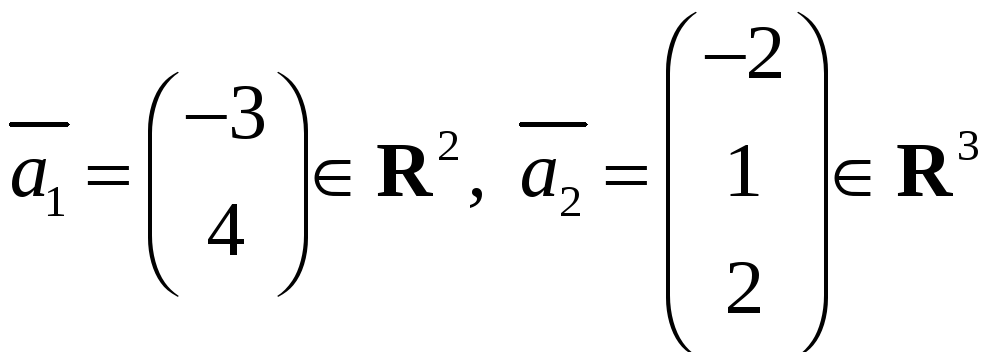Найти нормы этих векторов в соответствующих евклидовых пространствах, если скалярное произведение в каждом из них задано в стандартном виде

.

Пронормировать векторы согласно выбранной норме (построить соответствующие единичные векторы ).

Решение.

1) Норму вектора вычисляем по формуле

Вычисляем скалярное произведение

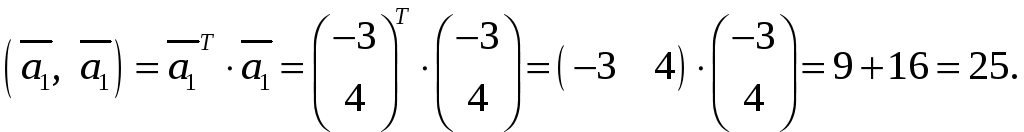
Тогда норма вектора равна

.

В результате нормированный вектор вычисляем по формуле

, .

2) Норму вектора вычисляем по формуле

Вычисляем скалярное произведение

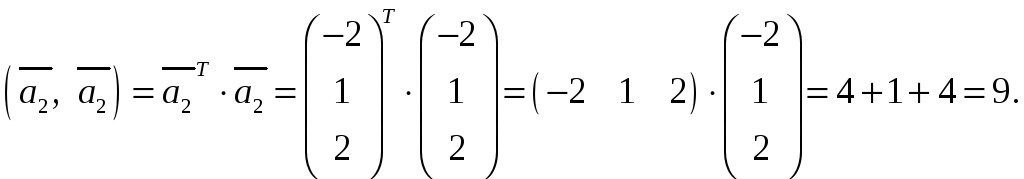
Тогда норма вектора равна

.

В результате нормированный вектор вычисляем по формуле

, .

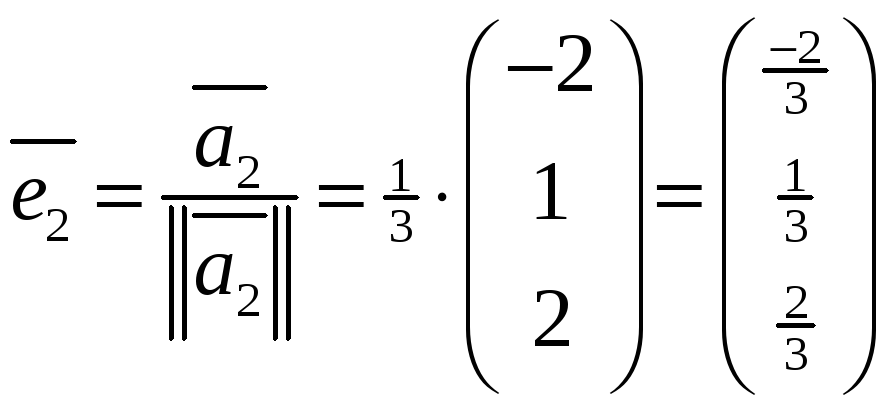Процесс ортогонализации Грама-Шмидта

Процесс построения ортонормированного базиса по произвольному базису называют процессом ортогонализации Грама-Шмидта. Процесс ортогонализации заключается в последовательном вычислении следующих векторов:

Составление ортогонального базиса	Процесс нормировки, получение ортонормированного базиса	Условия ортогональности векторов
	,
	,
	,	,
……………………………………	…………….……………	…………………
	, ,	, …………….

Пример 6. В пространстве со скалярным произведением задан базис :

.

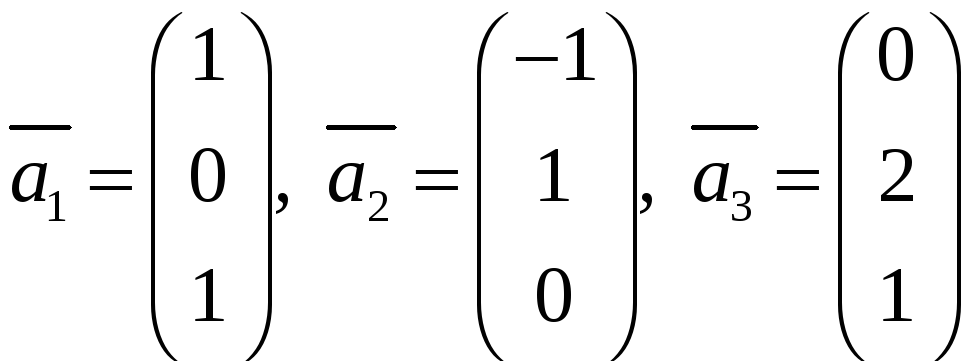Провести процесс ортогонализации Грама-Шмидта системы векторов базиса и составить ортонормированный базис .
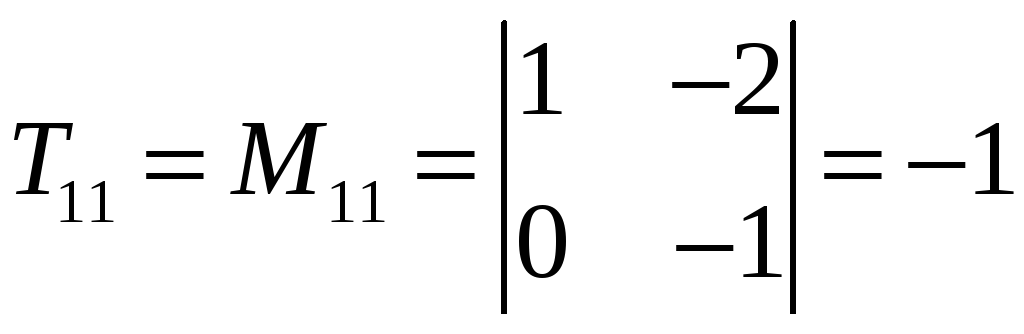
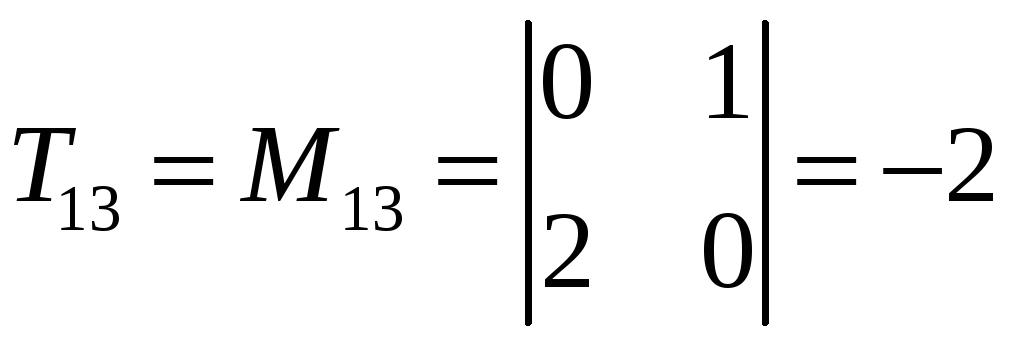
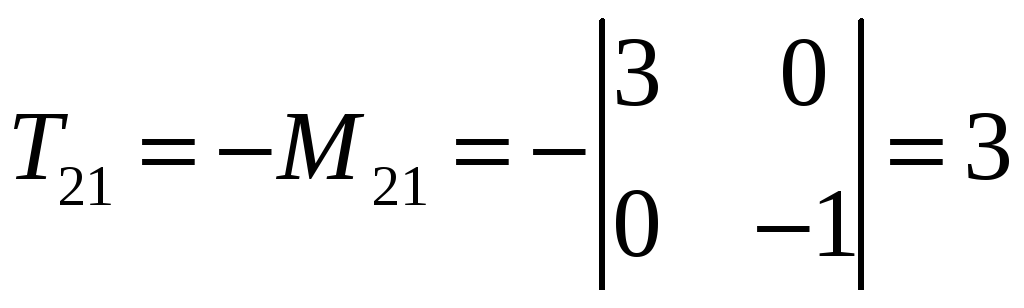
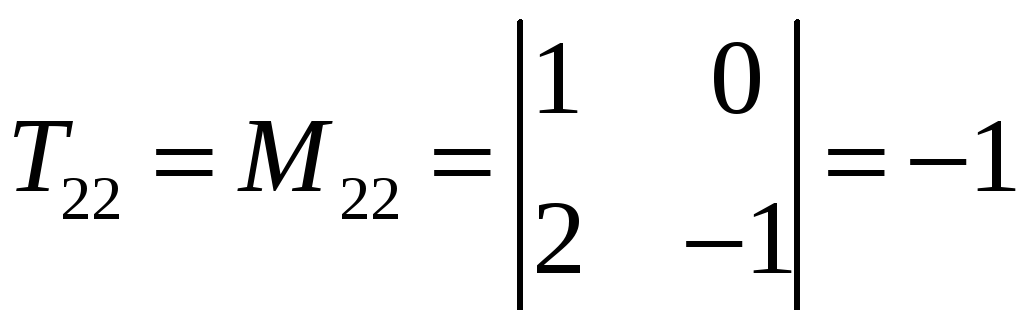
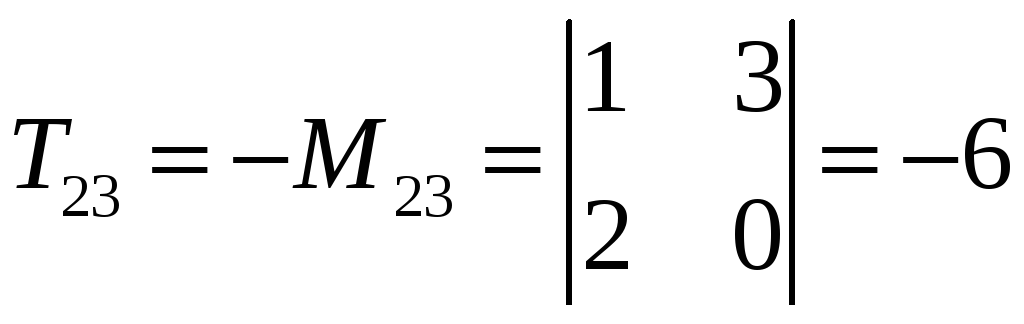
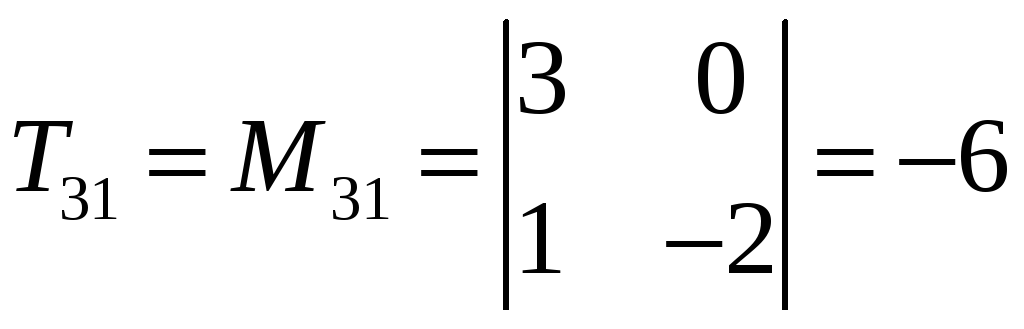
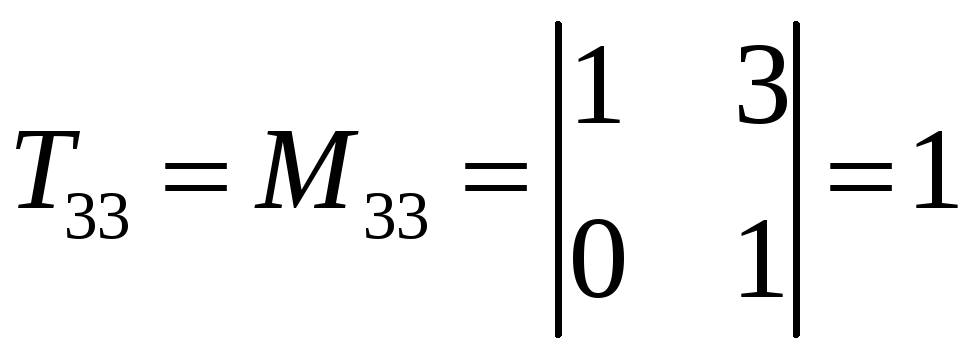
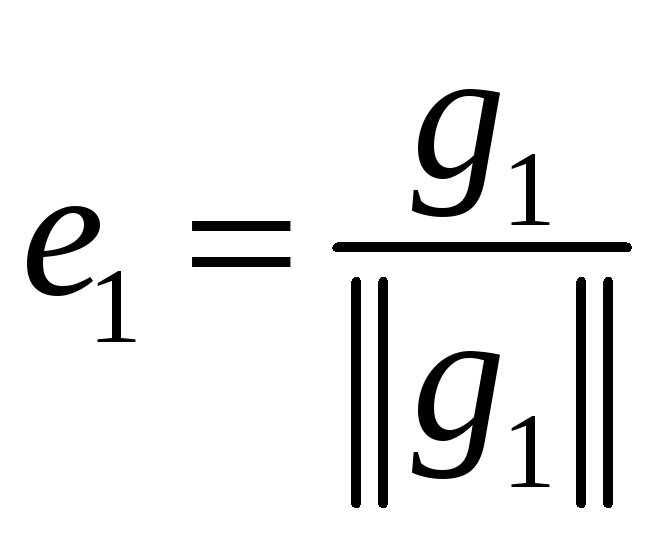
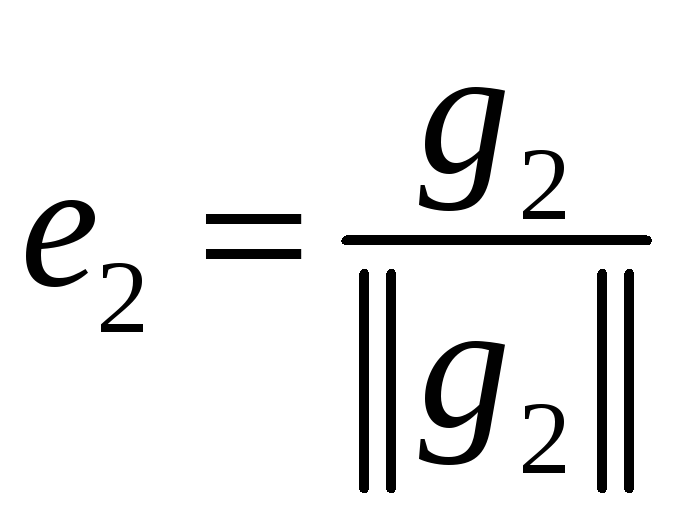
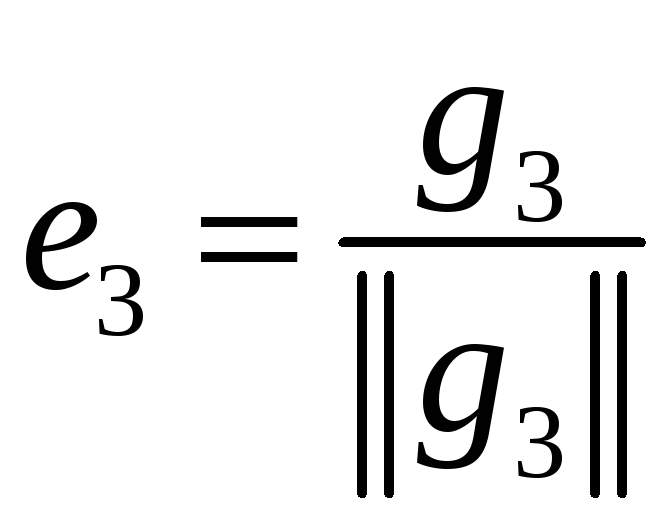
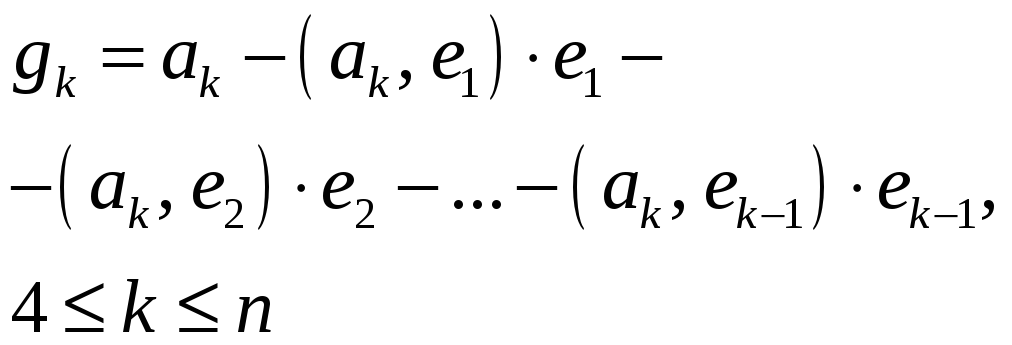