
Теоретические основы квантовых приборов
.pdf
числу нулей полинома |
Эрмита |
|
|
|
|
|
||||
по соответствующей |
|
координа- |
|
|
|
H0(x) |
|
|||
те. Они определяют распределе- |
1 |
|
|
|
|
|||||
|
|
|
|
|
||||||
ние поля в поперечном сечении |
|
H2(x) |
H1(x) |
|
|
|||||
пучка на зеркалах. |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|||
Мода резонатора |
обозна- |
0 |
|
|
|
|
||||
чается |
TEM mnq |
(Transverse |
|
|
|
H3(x) |
|
|||
|
|
|
|
|
||||||
Electromagnetic |
Wave |
– |
попе- |
– 1– 1 |
|
|
x |
1 |
||
речная электромагнитная волна) |
|
0 |
||||||||
|
|
|
|
|
||||||
и характеризуется тремя |
индек- |
|
|
Рис. 18 |
|
|
||||
сами. Продольный индекс q характеризует стоячую волну в направлении оси |
||||||||||
резонатора z, а индексы m и n характеризуют распределение интенсивности |
||||||||||
пучка света в поперечных направлениях x и y. Мода TEM 00q называется осе-
вой и имеет гауссовское распределение интенсивности (рис. 19). Примеры
распределения интенсивности света в модах TEM10q и TEM 21q также при-
ведены на этом рисунке. Чтобы определить распределение в конкретной моде, используют аналитическое представление уравнений (50) и (51) или же следующее правило: при чет-
ном индексе пятно находится |
y |
|
y |
|
|
y |
|
в центре по соответствующей |
|
|
|
|
|
|
|
координате, а число пятен в |
|
x |
|
x |
|
|
x |
направлении данной оси рав- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
но значению индекса попе- TEM00q |
TEM10q |
|
TEM32q |
||||
речной моды плюс единица. В |
|
|
|
|
|
|
|
случае круглых зеркал реше- |
|
|
Рис. 19 |
|
|
|
|
ние проводится в цилиндрической системе координат, ции выражаются через полиномы Лагерра.
2.3. Гауссовские пучки света в резонаторе
За пространственную границу пучка принимают поверхность, на которой при удалении от оси резонатора амплитуда поля падает в e раз (из-за
гауссовcкого множителя), а интенсивность поля при этом падает в e2 раз. Эта поверхность называется каустической поверхностью пучка света, для
31

продольной моды TEM 00q конфокального резонатора она представлена на
рис. 20. В случае прямоугольных зеркал она составлена из фрагментов четырех гиперболических цилиндров, а в случае круглых зеркал (случай осевой
|
|
|
|
|
симметрии) |
представляется |
|
|
|
|
|
гиперболоидом |
вращения. |
|
0 |
|
|
|
Волновые фронты поля пока- |
|
|
w |
|
|
|||
|
2 |
|
|
|
заны пунктирными линиями. |
|
2w |
|
0 |
L/2 |
z |
||
|
|
|
||||
-L/2 |
|
На зеркалах они совпадают со |
||||
|
|
|
|
|
||
|
|
|
|
|
сферической |
поверхностью |
|
|
|
|
|
зеркала, а в центре резонатора |
|
|
Рис. 20 |
|
|
фронт волны |
является плос- |
|
ким. Сечение пучка в центре резонатора, где оно минимально, называется перетяжкой гауссовского пучка. Полуширина пятна на зеркалах w определяется из (50) как
w = |
λL π |
. |
(52) |
Анализ собственных функций конфокального резонатора показывает, что гауссовские пучки обладают двумя основными свойствами – радиус волнового фронта в точке с продольной координатой z определяется только конфокальным параметром L
R(z) = z[1 + (L 2z)2 ]; |
(53) |
и радиус луча определяется радиусом перетяжки и конфокальным параметром
w(z) = w [1 + (2z L)2 |
]. |
(54) |
0 |
|
|
Используя эти свойства, можно определить основные параметры гауссовских пучков, представляющих моды конфокального резонатора. Из рис. 20 следует, что продольная координата места расположения зеркала резонатора z = L / 2 . Подставим это значение в (54) и, используя (52), найдем радиус перетяжки:
w0 = |
λL 2π |
. |
(55) |
Из (53) следует, что минимальное значение радиуса кривизны волнового фронта находится на зеркалах и составляет R(L 2) = L . Очень важным параметром является угол расходимости φ излучения в дальней волновой зоне (на большом расстоянии от резонатора – рис. 21). Значения этого угла составляют порядка нескольких угловых минут. Поэтому заменяем sin ϕ ≈ ϕ и вычисляем с учетом (53) – (60) угол расходимости
2) = L . Очень важным параметром является угол расходимости φ излучения в дальней волновой зоне (на большом расстоянии от резонатора – рис. 21). Значения этого угла составляют порядка нескольких угловых минут. Поэтому заменяем sin ϕ ≈ ϕ и вычисляем с учетом (53) – (60) угол расходимости
32

|
w(z) |
|
2w0 |
|
|
|
|
|
ϕ = lim |
= |
= |
|
2λ |
. |
|||
|
|
|
||||||
z →∞ R(z) |
|
L |
πL |
|||||
φ
2w
Таким образом, в резуль- |
z |
0 |
R |
тате анализа конфокального ре- |
|
зонатора можно получить пол- |
Рис. 21 |
ную информацию о структуре |
|
поля внутри и вне резонатора. Данные результаты являются основой для получения информации и о структуре поля произвольного резонатора. Для это-
го используют метод эквивалентного конфокального резонатора.
Рассмотрим волновые фронты гауссовского пучка (рис. 22). В любом резонаторе они должны совпадать с поверхностями зеркал. Пусть заданы параметры произвольного резонатора R1 , R2 и L. В нем существует гауссов-
ский пучок с конфокальным па- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
раметром Lэ, назовем это значе- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
R1 |
|
|
|
|
|
|
|
R2 |
|
|
|
|||||
ние |
эквивалентным |
конфокаль- |
|
|
|
|
|
|
|
|
|
|
|
|
||||
ным |
параметром |
резонатора. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Данное поле вместе с зеркалами |
|
|
|
|
|
|
|
|
|
|
|
|
z2 |
|
|
|||
резонатора представлено на рис. |
|
|
z1 |
|
|
|
|
|
|
0 |
|
|
|
z |
||||
2 Будем считать, что z1 и z2 по- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
ложительны, если |
перетяжка |
|
|
|
|
|
|
|
Lэ |
|
|
|
|
|||||
|
|
|
|
|
L |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
||||||||||
находится между зеркалами ре- |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
зонатора. Запишем радиусы кри- |
|
|
|
|
|
|
|
Рис. 22 |
|
|
|
|||||||
визны волновых фронтов в ме- |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
стах расположения зеркал: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
R = z [1 + (L |
э |
2z )2 |
], |
|
|
|
|
|
|
|
|
|||||
|
|
|
1 |
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
+ (Lэ 2z2 )2 ], |
|
|
|
||||||||||
|
|
R2 = z2 [1 |
|
|
|
|||||||||||||
|
|
L = z |
2 |
+ z . |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
В результате получим систему трех уравнений, решения которых можно записать через параметры конфигурации (45) (i, k = 1, 2):
L = |
2L |
|
|
|
, |
|
|||
gi gk (1 − gi gk ) |
|
||||||||
|
|
|
|
|
|
|
|||
э |
|
|
gi + gk |
− 2gi gk |
|
||||
|
|
|
(56) |
||||||
|
|
|
|
gk (1 |
− gi ) |
||||
|
= L |
|
|
||||||
zi |
|
|
. |
|
|
|
|||
gi + gk |
|
|
|
|
|||||
|
|
|
− 2gi gk |
|
|||||
|
33 |
|
|
|
|
|
|||

Параметры (56) полностью описывают гауссовский пучок, который формируется в резонаторе. Подставим зависимость w(z) в (50) согласно (54):
U m (x,
U n (y,
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
x 2 |
|
x |
||||
z)= C |
|
H |
|
exp − |
|
, |
||||
|
|
|
|
|||||||
|
m |
|
m w(z) |
|
w2 (z ) |
|||||
|
|
|
|
|
|
|
|
|
|
|
z )= C |
|
|
|
|
|
|
|
|
2 |
|
|
H |
|
2 |
y |
||||||
|
|
y |
exp − |
|
. |
|||||
|
n |
|
n |
w(z ) |
|
w2 (z ) |
||||
|
|
|
|
|
|
|
|
|
|
|
Данные выражения описывают распределение амплитуды электромагнитного поля гауссовского пучка в любой точке пространства. Это поле определяется только одним параметром – конфокальным параметром пучка L.
2.4. Частоты мод и потери в резонаторах
Анализ спектра частот резонатора методом, описанным в 3, дает для произвольного резонатора следующее выражение для частоты моды (из условия баланса фаз):
ν |
|
= |
c |
[q + π−1(1 + m + n)arccos |
|
|
] |
. |
(57) |
|
mnq |
g g |
2 |
||||||||
|
||||||||||
|
|
2L |
1 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
||
Отсюда получаем спектр частот конфокального резонатора
ν mnq = c [q + (1 + m + n)]. 4L
Из этого выражения следует, что частотный спектр конфокального резонатора является вырожденным. Интервал между соседними частотами спектра составляет c/4L, что связано с кратностью интервала между продольными модами (равного c/2L, как и в остальных типах резонаторов) интервалу между поперечными модами конфокального резонатора (равному c/4L).
Интересно сравнить этот спектр (рис. 23, б) со спектром плоскопараллельного резонатора (рис. 23, а), который не может быть получен из общего выражения (57), так как рассчитывается в приближении плоских волн. Результат этого расчета дается выражением
νmnq = |
c |
q |
+ |
1 |
|
(m2 + n |
2 ) L |
|
|
|||
|
|
|
|
|
|
|
|
|
. |
(58) |
||
|
|
2 |
|
q |
|
|
4a2 |
|||||
|
2 L |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
34
Спектры продольных мод TEM00q этих резонаторов совпадают, но поперечные моды в плоскопараллельном резонаторе располагаются группами вокруг продольной моды.
Частотные интервалы между соседними поперечными модами плоскопараллельного резонатора из-за нелинейности соотношения (58) по m и n не являются эквидистантными. Они определяются согласно выражению
νm = |
c |
|
L2 |
(m + 1/ 2) = νq |
m + 1/ 2 |
, |
|
2L 4qa2 |
|
||||||
|
|
|
8N |
||||
где N – число Френеля, а |
ν q = c / 2L . |
||||||
10q
00q 00q+1
 11q
11q
c/2L
a
00q |
10q |
00q+1 |
|
01q |
20q |
б
Рис. 23
Отметим, что в плоскопараллельном резонаторе тоже есть частотное вырождение мод (поперечных), поскольку частоты мод с одинаковым значе-
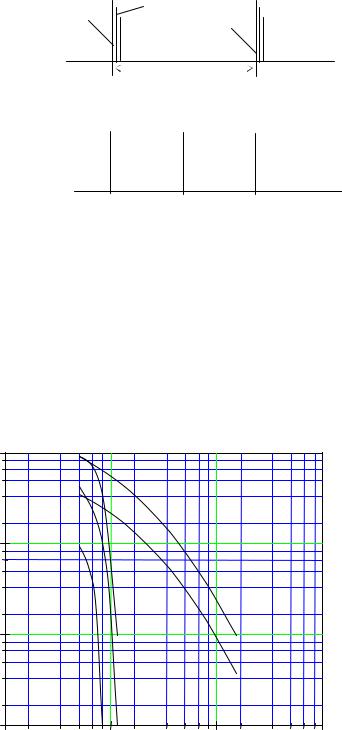
нием m2 + n 2 совпадают. Потери в резонато-
рах различного типа обычно определяются с помощью численных решений соответствующих уравнений. Результаты их решений для плоскопараллельного и конфокального резонаторов приведены на рис. 24.
На практике используют устойчивые резонаторы со значениями параметров конфигурации, находящимися в диапазоне
1
, % |
|
энергииПотери |
0.1 |
|
0.01
TEM20q TEM10q
TEM00q TEM10q TEM00q
1E-3
0.1 |
1 |
10 |
100 |
Рис. 24
35

0 < g1 < 1… 0 < g2 1< , которые имеют минимальные потери, почти не зависящие от слабой разъюстировки зеркал. Одно из зеркал резонатора (выходное) выбирается плоским, а второе – с радиусом кривизны R > L.
В кольцевых резонаторах используют симметричные схемы, чтобы избежать появления невзаимности встречных волн, – в треугольном резонаторе
– одно сферическое зеркало и два плоских, а в четырехугольном – два сферических и два плоских.
Для управления добротностью резонатора в режиме генерации импульсов широко используют электрооптические затворы. Основным звеном таких затворов являются электрооптические элементы, выполненные в виде ячейки Керра или ячейки Поккельса.
Ячейка Керра представляет собой конденсатор, диэлектрическая компонента которого обладает свойством приобретать двойное лучепреломление под действием электрического поля (эффект Керра). Вещество в ячейке под воздействием электрического поля становится в оптическом отношении подобным одноосному кристаллу с оптической осью вдоль направления электрического поля. Разность показателей преломления обыкновенного no и необыкновенного ne лучей пропорциональна квадрату напряженности элек-
трического поля E: no - ne = lBE 2 (l – длина волны света; B – постоянная Керра). В результате разность фаз, приобретаемая лучами на ячейке длиной l,
равна j = 2lπ l (no - ne ) = 2p B lE 2 . В ячейках Керра широко используется
нитробензол, имеющий большую постоянную Керра B = 4 ×10−5 B− 2 см. Ячейка Поккельса представляет собой помещенный в электрическое
поле кристалл, обладающий электрооптическим эффектом.. Наиболее часто в качестве рабочего тела используют одноосные кристаллы фосфида калия (КДР), его дейтерированный вариант (ДКДП) и ряд других. Кристалл устанавливают так, чтобы луч света проходил вдоль оптической оси z (рис. 25) При этом в отсутствие внешнего модулирующего поля свет любой поляризации распространяется с одной той же скоростью. Если приложить внешнее электрическое поле E вдоль оси z показатели преломления волн с ортого-
нальными поляризациями, направленными под углом ± 45 к кристаллографическим осям x и y, оказываются различающимися на величину, пропорциональную полю E. Таким образом, разность фаз, приобретаемая этими вол-
36

нами в кристалле, является линейной функцией поля, в отличие от эффекта Керра, где она пропорциональна квадрату поля.
Активный элемент |
Поляризатор |
Ячейка Поккельса |
||
|
|
|
|
|
|
|
|
|
|
x E
y
Рис. 25
Для управления добротностью резонатора ячейку и поляризационную призму помещают в резонатор вместе между активным элементом и зеркалом (рис. 25). Призму ориентируют так, чтобы ее главная плоскость составляла угол 45° с направлением поля в случае ячейки Керра. Если применяется ячейка Поккельса, призму ориентируют так, чтобы ее главная плоскость совпадала с одной из кристаллографических осей x или y электрооптического кристалла. К ячейке прикладывают напряжение такой величины, чтобы разность хода обыкновенного и необыкновенного лучей составляла половину длины волны. В результате плоскость поляризации света при прохождении лучом ячейки туда и обратно повернется на 90° относительно первоначального направления, задаваемого поляризационной призмой, и свет не сможет пройти через нее. Это соответствует закрытому состоянию затвора, т. е. разрыву обратной связи. При снятии напряжения с ячейки затвор открывается, потери в резонаторе резко падают и обратная связь в нем восстанавливается. Время переключения электрооптических затворов составляет единицы наносекунд.
Для осуществления режима генерации “ гигантского импульса” в твердотельных лазерах широко используются пассивные просветляющиеся затворы и насыщающиеся фильтры. Их действие основано на свойстве некоторых веществ изменять прозрачность под действием проходящего через них оптического излучения. В качестве пассивного затвора используют кювету, заполненную просветляющейся жидкостью (растворы фталоциана или полиметиловых красителей), или пластину из стекол с примесью селена и кадмия или же солей урана. В такой среде поглощение уменьшается с ростом интенсивности излучения. Введение в резонатор просветляющегося затвора увели-
37
чивает потери и, следовательно, повышает пороговый уровень накачки. В результате в активной среде происходит значительное накопление частиц на верхнем рабочем уровне. Одновременно растет и мощность спонтанного излучения с этого уровня, что приводит к увеличению прозрачности затвора. Когда она достигает такого значения, при котором выполняется условие самовозбуждения, происходит регенеративный лавинообразный процесс нарастания амплитуды колебаний и вся запасенная в активной среде энергия излучается в виде мощного импульса длительностью несколько наносекунд. По окончании импульса генерации молекулы затвора релаксируют в исходное состояние и он восстанавливает свои оптические свойства.
Из других методов управления добротностью резонатора отметим использование резонаторов, в которых модуляция добротности достигается вращением одного из зеркал вокруг оси, расположенной в плоскости зеркала.
3. ЭЛЕМЕНТЫ ТЕОРИИ ЛИНЕЙНОГО ЛАЗЕРА
3.1. Основные уравнения газового лазера
Задача анализа режимов работы и определения характеристик газовых лазеров решается в рамках полуклассической теории лазера, разработанной американским ученым У. Лэмбом. В этой теории электромагнитное поле рассматривается классически, а активное вещество – с точки зрения квантовой механики. Общая логика решения задачи состоит в том, что электромагнитное поле, существующее в резонаторе, рассматривается в качестве источника поляризации активной среды, которая, в свою очередь, является источником электромагнитного поля за счет процессов индуцированного излучения. Таким образом, задача является самосогласованной.
Самосогласованные уравнения электромагнитного поля в резо-
наторе лазера. Классическое электромагнитное поле описывается уравнениями Максвелла:
div D = 0; |
rot E = − |
∂B ; |
|
|
|
|
∂t |
∂D ; |
|
div B = 0; |
rot H = J + |
(59) |
||
|
|
|
∂t |
|
D = ε0E + P; B = μ0H; J = σE.
38
В качестве граничного условия используется периодичность поля при обходе резонатора. Потери энергии в резонаторе вводятся эквивалентной усредненной по длине резонатора проводимостью σ = ε0ω Q n .
Q n .
Анализ продольных мод оптических резонаторов показал, что зависимость электромагнитного поля от поперечных координат в масштабе, сравнимом с длиной волны, является слабой. Поэтому будем представлять электромагнитное поле как суперпозицию плоских волн, записывая пространственную часть моды резонатора в виде U n (z) = sin kn z , где индекс продольной моды здесь будет обозначен как n, а kn – волновое число моды. Тогда проекции напряженности поля и поляризации на ось резонатора можно разложить по продольным модам резонатора:
E(z,t ) = ∑ An (t )U n (z);
n |
(60) |
P(z,t ) = ∑ Pn (t )U n (z).
n
Напомним, что под поляризацией среды понимают значение дипольного момента единицы объема вещества. Для неполярных диэлектриков, какими являются газы, она полностью определяется суммарным значением дипольного момента квантовых систем, наведенного внешним электромагнитным полем. Из (60) для волны продольной моды можно получить волновое уравнение
∂ 2 A |
(t ) |
+ |
σ |
∂A |
(t ) |
+ fn2 An (t ) = − |
1 |
∂ 2 P |
(t ) |
|
n |
|
|
n |
|
|
n |
, |
(61) |
||
|
ε0 |
|
|
|||||||
∂ t 2 |
|
|
∂ t |
|
ε0 ∂ t 2 |
|
||||
где fn – круговая частота n-й моды резонатора. Поскольку источником поляризации является квазимонохроматическое электромагнитное поле моды
резонатора, с большой точностью можно сделать замену |
∂ 2 P (t ) |
= − f |
2 P (t ). |
n |
|||
|
∂ t 2 |
|
n n |
|
|
|
|
Для анализа волнового уравнения (61) воспользуемся приближением |
|||
медленно меняющихся фаз и амплитуд: |
|
|
|
An (t ) = En (t )cos[ωnt + ϕn (t )]; |
|
|
(62) |
Pn (t ) = Cn (t )cos [ωnt + ϕn (t )]+ Sn (t )sin [ωnt + ϕn (t )]. |
|
|
|
Здесь Cn (t) и Sn (t) – амплитуды синфазной и квадратурной по отношению к полю En (t) компонент поляризации. Эти величины вместе с ϕn (t) являются
39

медленно меняющимися по сравнению с периодом колебаний электромагнитного поля оптической частоты функциями времени.
Подстановкой (62) в (61) получаем самосогласованные уравнения электромагнитного поля в резонаторе:
(ωn |
+ ϕn (t ) − fn )En (t ) = − |
1 ωn |
Cn (t ), |
(63) |
|||||||||
|
ɺ |
|
|
|
|
|
|
|
|
||||
|
|
|
|
2 ε0 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
||||
Eɺn (t ) + |
1 |
|
ωn |
En (t ) = − |
1 |
|
ωn |
Sn (t ). |
(64) |
||||
2 Qn |
|
|
|||||||||||
|
|
2 |
|
ε0 |
|
|
|||||||
Эти уравнения определяют амплитуды и фазы электромагнитного поля в резонаторе лазера, если известны значения коэффициентов поляризации Cn (t) и Sn (t). Задача определения поляризации активной среды решается далее.
Квантовомеханическое описание взаимодействия активной среды и электромагнитного поля. В квантовой механике описание состояния вещества ведется с помощью волновых функций. Их физический смысл определяется следующим образом. Каждой физической величине приводится в соответствие определенный математический линейный эрмитовый оператор, собственными функциями которого являются волновые функции состояния Ψ , а собственными значениями – числовые значения физической величины. Описание состояний с помощью волновой функции дает информацию не о действительном состоянии системы, а о возможном, так как величина
ΨΨ = Ψ 2 имеет смысл вероятности нахождения системы в данном состоянии. Волновые функции являются решениями уравнения Шредингера
HΨ = i ∂Ψ . (65)
∂ t
где H – оператор Гамильтона, или оператор полной энергии системы. Для изолированной двухуровневой квантовой системы он имеет вид
|
E |
0 |
|
|
|
|
a |
|
|
H = |
0 |
E |
, |
|
0 |
|
|
||
|
|
|
b |
|
Ea и Eb – значения энергии квантовой системы, находящейся, соответственно, на верхнем или на нижнем уровне.
Так описываются так называемые чистые состояния – состояния, полностью характеризующиеся определенными набором квантовых чисел и значением энергии квантовой системы. Но в активной среде, представляющей
40
