
ДС Радиооптика_1 / Литература ч.1 / 72
.pdf
[( |
|
|
mez ) |
nez ]dl |
|
[ ( m n ) |
nez ( |
mez )]dl |
||
L |
|
|
|
|
|
|
|
L |
|
|
|
|
|
n |
|
|
m |
dl |
0. |
|
|
|
|
m |
n |
n |
n |
|
|
|||
|
|
|
|
|
|
|||||
|
L |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
Таким образом,
H |
m |
H* |
dS 0, m n. |
|
n |
|
S
Наконец, найдем
I |
EH |
(E |
m |
H* |
)e |
dS i |
* |
[ |
n |
( |
n |
e |
z |
)]e |
dS. |
|
|
n |
z |
|
m n |
|
|
|
z |
|
|||||
|
|
S |
|
|
|
|
|
S |
|
|
|
|
|
|
|
Раскрыв двойное векторное произведение, найдем:
I |
EH |
i |
m n |
[ ( |
m n |
e |
z |
) |
n |
e |
z |
2 |
]e |
dS i |
m n |
k 2 |
m n |
dS. |
|
|
|
|
|
|
m |
z |
|
m |
|
||||||||
|
|
|
|
S |
|
|
|
|
|
|
|
|
|
|
|
|
S |
|
(Первое слагаемое в квадратных скобках равно нулю, так как содержит
 Отформатировано: По ширине скалярное \ произведение двух взаимно перпендикулярных
Отформатировано: По ширине скалярное \ произведение двух взаимно перпендикулярных
векторов  m и
m и 
В результате имеем
(E m H* m )ez dS i |
m n k 2m m n dS 0 m n. |
(3.72) |
S |
|
|
S
Последнее равенство означает, в частности, что
 электромагнитные волны различных типов распространяются в ЛП независимо друг от друга, и суммарная мощность, переносимая всеми волнами, равна сумме мощностей, переносимых каждой волной.
электромагнитные волны различных типов распространяются в ЛП независимо друг от друга, и суммарная мощность, переносимая всеми волнами, равна сумме мощностей, переносимых каждой волной.
Действительно, пусть в ЛП распространяется N различных типов Е-волн. Тогда поле в ней представляет собой суперпозицию полей этих волн:
Отформатировано: По ширине
N |
N |
E |
Em ; H Hm . |
m 1 |
m 1 |
Переносимая мощность равна действительной части потока вектора
 Пойнтинга:
Пойнтинга:
Отформатировано: По ширине
|
|
|
N N |
|
|
|
N |
P 0.5Re (E H* )e |
dS |
0.5Re |
(E |
m |
H* )e |
dS |
P , |
z |
|
|
|
n z |
|
m |
|
S |
|
|
m 1 n 1 S |
|
|
|
m 1 |
где |
|
|
|
|
|
|
|
Pm 0.5 Re |
(Em |
H*m )ez dS — |
|
(3.73) |
|||
|
|
S |
|
|
|
|
|
102

мощность, переносимая волной с номером т. Величину
|
Nm |
(Em |
|
H*m )ez dS |
|
k k 2 e 2 z |
|
|
| |
|
m |2 |
|
dS, |
|
|
(3.74) |
|
||||||
пропорциональную |
S |
|
|
|
|
|
|
|
|
|
|
|
S |
|
нормой |
собственной |
|
||||||
мощности Рт, называют |
|
Отформатировано: По ширине |
|||||||||||||||||||||
волны. Используя первую формулу Грина (П1.26), найдем |
|
|
|
||||||||||||||||||||
|
|
|
Nm |
|
|
k m e 2 |
z |
| |
|
m |2 |
dS. |
|
|
|
|
|
(3.75) |
|
|||||
|
|
|
|
|
|
|
|
|
|
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
Можно |
убедиться, |
|
что |
|
соотношения |
|
ортогональности |
Отформатировано: По ширине |
|||||||||||||||
справедливы для Н-волн, а также и в том случае, когда одна из волн |
|
||||||||||||||||||||||
принадлежит к волнам Е-типа, а другая — к волнам Н-типа. Что |
|
||||||||||||||||||||||
касается гибридных волн, то, в силу граничных условий, оператор |
|
||||||||||||||||||||||
Лапласа для них не является самосопряженным и может иметь |
|
||||||||||||||||||||||
комплексные собственные значения. Поэтому для гибридных волн |
|
||||||||||||||||||||||
соотношения ортогональности, вообще говоря, не справедливы. |
|
||||||||||||||||||||||
Площадь поперечного сечения S открытых линий передачи не |
|
||||||||||||||||||||||
ограничена, поэтому поверхностные интегралы могут расходиться. |
|
||||||||||||||||||||||
Соотношения ортогональности в этом случае не выполняются. Однако, |
|
||||||||||||||||||||||
если поле собственных волн в открытой ЛП достаточно быстро |
|
||||||||||||||||||||||
убывает в поперечном направлении, интегралы при S |
|
имеют |
|
||||||||||||||||||||
конечный предел и такие волны обладают свойством ортогональности. |
|
||||||||||||||||||||||
Если в ЛП наряду с волнами, распространяющимися в |
|
||||||||||||||||||||||
положительном направлении оси z (падающими), имеются волны, |
|
||||||||||||||||||||||
распространяющиеся в обратном направлении (отраженные), то |
|
||||||||||||||||||||||
соотношение ортогональности (3.72) необходимо обобщить. |
|
||||||||||||||||||||||
Обозначим волны, распространяющиеся в отрицательном направлении |
|
||||||||||||||||||||||
оси z, отрицательными индексами. Так как распределение поля |
|
||||||||||||||||||||||
падающих и отраженных волн в поперечном сечении одинаково, – |
|
||||||||||||||||||||||
m = m, k –m = k m, k||–m= – k||m. Используя эти соотношения, вычислим |
|
||||||||||||||||||||||
|
|
|
I |
[(E |
m |
|
H* |
) (E |
n |
H* |
|
)e |
dS. |
|
|
|
|
|
|
||||
|
|
|
S |
|
|
|
n |
|
|
m |
|
z |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Воспользовавшись (3.72), получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
I i ( |
m n |
k 2 |
n m |
k 2 |
) |
|
m n |
dS i |
(k |
m |
k 2 |
|
k |
n |
k 2 |
) |
m n |
dS. |
|
||||
|
n |
m |
|
S |
|
|
|
n |
|
m |
S |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
103

Если m n, то интеграл в правой части равен нулю и I = 0. Если п = т,
 то выражение в круглых скобках равно нулю и I также равно нулю.
то выражение в круглых скобках равно нулю и I также равно нулю.
При п = –т
Отформатировано: По ширине
|
|
|
I 2 |
|
m |
| |
m |2 dS Nme |
|
0. |
|
|
|||
|
|
|
|
|
|
S |
|
|
|
|
|
|
|
|
Таким образом, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[(E |
m |
H* |
) |
(E |
n |
H* |
)e |
dS |
0, |
|
n |
m . |
(3.76) |
|
|
n |
|
|
m |
z |
|
e |
, |
n |
m |
|
||
S |
|
|
|
|
|
|
|
|
|
Nm |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Соотношение (3.76) есть обобщенное условие ортогональности
 Отформатировано: По ширине волн в ЛП. Проделав соответствующие выкладки, его нетрудно получить и для Н-волн, а также для случая, когда одна из волн принадлежит к волнам Е-типа, а другая — к волнам Н-типа.
Отформатировано: По ширине волн в ЛП. Проделав соответствующие выкладки, его нетрудно получить и для Н-волн, а также для случая, когда одна из волн принадлежит к волнам Е-типа, а другая — к волнам Н-типа.
Величину Nem называют обобщенной нормой волны. Сравнивая (3.75) и (3.76), видим, что в ЛП без потерь для распространяющихся
типов волн (k||m= m)
Nem = 2Nm.
Для не распространяющихся типов волн (k||m = – i m)
Nme 2 i | Nm | e2 z 2 i m |
| |
m |2 dS — |
|
S |
|
мнимая величина, не зависящая от координаты z. Заметим, что в линии
 Отформатировано: По ширине передачи с потерями обобщенная норма Nem в отличие от Nm также не
Отформатировано: По ширине передачи с потерями обобщенная норма Nem в отличие от Nm также не
зависит от координаты z. Поэтому обобщенную норму удобнее использовать при анализе распространения волн в линиях передачи.
3.8. Передаваемая мощность и затухание волн в линиях передачи
Мощность, переносимая падающей волной определенного типа в
 Отформатировано: По ширине линии передачи определяется потоком вектора Пойнтинга через ее
Отформатировано: По ширине линии передачи определяется потоком вектора Пойнтинга через ее
поперечное сечение S:
|
|
P |
|
1 |
Re (E H* )ez dS. |
(3.77) |
|
|
|
2 |
|
||||
|
|
|
S |
|
|
||
|
|
|
|
|
|
|
|
В общем случае напряженности электрического и магнитного полей |
Отформатировано: По ширине |
||||||
имеют |
как |
поперечные, |
|
|
так и продольные составляющие: |
|
|
E E |
Ezez ; |
H H Hzez . |
Подставив эти выражения в (3.77) и |
|
|||
произведя перемножение, получим |
|
|
|||||
104

|
|
P |
1 |
Re |
|
(E |
H* )ez dS, |
|
|
(3.78) |
|
||||
|
2 |
S |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Как видно, мощность передается только поперечными составляющими |
Отформатировано: По ширине |
||||||||||||||
электромагнитного поля волны. Поскольку вклад в энергию, |
|
||||||||||||||
запасенную в единице длины линии передачи W1, вносят |
все |
|
|||||||||||||
составляющие электромагнитного поля, скорость переноса |
энергии |
|
|||||||||||||
vэ = P/W1 у волн, |
имеющих продольные |
составляющие |
поля |
(и, |
|
||||||||||
следовательно, обладающих дисперсией), всегда меньше, чем у |
|
||||||||||||||
поперечных волн (волн типа T). |
|
|
|
|
|
|
|
|
|
|
|||||
Используя связь (3.49) между поперечными составляющими поля |
|
||||||||||||||
в ЛП, формулу (3.78) можно переписать следующим образом: |
|
|
|
||||||||||||
P |
|
1 |
|
| E | |
2 |
dS |
1 |
Re Zc |
S | H | |
2 |
dS. |
93.79) |
|
||
|
2 Re Zc S |
|
2 |
|
|
||||||||||
С помощью выражений (3.45) – (3.49), выразим передаваемую
 мощность через мембранную функцию. Для E- и T-волн имеем
мощность через мембранную функцию. Для E- и T-волн имеем
Отформатировано: По ширине
P |
0.5 Re(k*k / Z0 ) e 2 z |
| |
e |2 |
dS. |
(3.80) |
|
|
|
|
|
S |
|
|
|
|
Для H-волн получаем |
|
|
|
|
|
|
|
P |
0.5 Re(kk *Z0 ) e 2 z |
| |
m |2 |
dS. |
(3.81) |
|
|
|
|
S |
|
|
|
|
|
Для многих технических приложений важно |
максимальную |
Отформатировано: По ширине |
|||||
мощность, которую можно передать по данной линии передачи. Как |
|
||||||
следует из формул (3.45), (3.47), напряженность электрического поля в |
|
||||||
ЛП пропорциональна мембранной функции. Поэтому по мере |
|
||||||
увеличения передаваемой |
мощности |
растет |
напряженность |
|
|||
электрического поля в ЛП, что может привести к электрическому |
|
||||||
разряду (пробою) в заполняющей линию среде. Ввиду высокой |
|
||||||
концентрации электронов в области разряда ее сопротивление очень |
|
||||||
мало, и волна практически полностью отражается от разрядного |
|
||||||
промежутка, т. е. передача энергии по ЛП прекращается. Кроме того, |
|
||||||
высокая температура в области разряда может привести к разрушению |
|
||||||
линии передачи. Поэтому значение пробивной напряженности |
|
||||||
электрического поля Eth является одним из важных параметров ЛП. |
|
||||||
Оно зависит от заполняющей |
волновод |
среды, частоты и других |
|
||||
105

факторов. Для волноводов с газовым заполнением пробивная напряженность определяется, прежде всего, химическим составом газа и его давлением. Например, для сухого воздуха при атмосферном давлении и нормальной ионизации Eth = 30 кВ/см. Пробивная напряженность может быть повышена за счет увеличения давления и (или) использования газов с другим химическим составом. Так, элегаз (SF6) имеет, при прочих равных условиях, пробивную напряженность в 6 раз большую, чем воздух.
За счет потерь в среде и в стенках ЛП происходит нагрев элементов ее конструкции, и при определенной мощности они начинают разрушаться. Происходит так называемый тепловой пробой. Эти явления и ограничивают максимальную передаваемую мощность. Для расчетов вводят понятия предельной мощности Pth, при которой возникает электрический или тепловой пробой, и допустимой мощности Pmax, которая обычно в 3…5 раз меньше предельной. При передаче коротких импульсов электрический пробой наступает, как правило, раньше теплового, поэтому предельная мощность определяется пробивной напряженностью поля. Если ЛП работает в непрерывном режиме, предельная мощность, в зависимости от типа и конструкции ЛП, может быть ограничена как электрическим, так и тепловым пробоем.
Распространение электромагнитной волны в ЛП сопровождается рассеянием части ее энергии как в среде, заполняющей линию передачи, так и на поверхности входящих в ее конструкцию металлических проводников. Вследствие этого амплитуда волны по мере распространения уменьшается, т. е. волна, как это вытекает из выражений (3.80), (3.81), экспоненциально затухает.
При расчете затухания в ЛП необходимо учитывать, что диэлектрическая и (или) магнитная проницаемость заполняющей ее среды комплексны, так что волновое число k = k'-ik'' и характеристическое сопротивление среды Zc — комплексные величины.
106

На металлических поверхностях электромагнитное поле удовлетворяет граничному условию Леонтовича (5.14). Подставив в него выражения (3.58), (3.59) и спроецировав полученное векторное уравнение на ось z и направление касательной к направляющей еl, получим два скалярных уравнения
|
|
|
|
|
|
|
m |
|
|
e |
|
|
||||
|
|
k 2 |
e |
i k Z |
|
|
|
|
|
i kZ Y |
|
|
; |
|
|
|
|
|
|
s |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
l |
s 0 |
n |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
e |
|
|
m |
|
|
||||
|
|
k 2 |
m |
i k Z |
|
|
|
|
i kZ Y |
|
|
. |
|
|
||
|
|
|
s |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
l |
s 0 |
n |
|
|
||||||
из которых следует, что при Zs |
|
|
|
|
|
|
||||||||||
|
|
0 в ЛП распространяются гибридные |
Отформатировано: По ширине |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
волны. |
Этот |
эффект |
|
впервые |
был |
подробно |
исследован |
|
||||||||
Б. З. Каценеленбаумом в 1953 г. Отметим, что если для данной волны |
|
|||||||||||||||
/ l = 0, |
она |
распространяется |
в |
ЛП с |
конечной проводимостью |
|
||||||||||
стенок "в чистом виде", без примеси волн другого типа. |
Если |
|
||||||||||||||
поверхностное |
сопротивление |
|
Zs |
достаточно мало, то можно |
|
|||||||||||
пренебречь вторыми членами в левой части записанных равенств. В |
|
|||||||||||||||
таком приближении граничные условия для Е- и Н-волн разделяются: |
|
|||||||||||||||
|
|
|
e |
|
m |
|
||
k 2 |
e i kZ Y |
|
0; k 2 |
m i kZ Y |
|
0, |
(3.82) |
|
|
|
|||||||
|
s |
0 |
n |
s 0 |
n |
|
||
|
|
|
|
|
||||
«Примесь» волн другого типа при этом не учитывается. |
|
|||||||
Подставив |
(3.82) |
в |
формулу |
(3.68), |
найдем, |
что значения |
||
критических волновых чисел, получаемых в результате решения уравнения (3.25) с граничными условиями Леонтовича, комплексны: k =k' + ik'' Таким образом, постоянная распространения
k|| = – i = [k'2 – k' 2 – k''2 + k''2 -2i(k'k'' + k' k'' )]1/2
также комплексна.
В случае малого затухания (k'' << k', k'' << k' ) величинами
 второго порядка малости можно пренебречь. Предполагая, кроме того, что
второго порядка малости можно пренебречь. Предполагая, кроме того, что
k'2 – k' 2 >> 2(k'k'' + k' k''), т. е. что частота не слишком близка к критической, преобразуем выражение для постоянной распространения следующим образом:
Отформатировано: По ширине
Отформатировано: По ширине
107

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k k |
|
k k |
|
|
|
|||||
|
|
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
k |
|
k |
|
k ' |
1 i |
|
|
|
|
|
. |
|
|
|
|||||||||||
|
|
|
|
|
k 2 |
k 2 |
|
|
|
||||||||||||||||||
Отсюда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
k 2 |
|
k 2 ; |
|
|
|
|
|
(3.83) |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
д |
|
м , |
|
|
|
|
|
|
(3.84) |
|
|||||
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k k |
|
|
|
|
|
|
|
|
|
k tg |
|
|
|
; |
|
|
(3.85) |
|
|||
|
|
|
д |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
/ k )2 |
|
|
|
|||||||
|
|
|
|
2 1 |
|
(k |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
k k |
|
|
|
|
|
|
|
|
|
k k |
|
|
|
— |
|
(3.86) |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
м |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
)2 1 |
|
|
|||||||
|
|
|
|
2 |
(k / k |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
постоянные |
затухания, |
обусловленные |
|
потерями в диэлектрике и |
Отформатировано: По ширине |
||||||||||||||||||||||
металле. В данном приближении эти потери и их можно вычислить |
|
||||||||||||||||||||||||||
независимо. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
При |
0 |
постоянные |
|
д |
и |
|
|
м |
|
стремятся к бесконечности. |
|
||||||||||||||||
Однако следует отметить, что при малых |
становится неприменимым |
|
|||||||||||||||||||||||||
приближение, для которого получены соотношения (3.83) – (3.86). На |
|
||||||||||||||||||||||||||
высоких частотах |
k' и выражение для |
d упрощается: |
м |
0.5k'tg , |
|
||||||||||||||||||||||
что совпадает с формулой (3.36) для плоской электромагнитной волны. |
|
||||||||||||||||||||||||||
Для определения необходимо решить уравнение (3.25) с |
|
||||||||||||||||||||||||||
комплексными граничными условиями третьего рода (3.82). Несколько |
|
||||||||||||||||||||||||||
примеров решения этой сложной задачи для простейших случаев |
|
||||||||||||||||||||||||||
приведены в монографии Л. Левина [16]. Более простой метод |
|
||||||||||||||||||||||||||
вычисления |
m |
основан на |
|
том, |
|
что |
для металлов |
с |
высокой |
|
|||||||||||||||||
электропроводностью толщина скин-слоя в микроволновом диапазоне составляет доли микрометра, а модуль коэффициента отражения практически равен единице (см. раздел 5.5). Это позволяет предполагать, что структура поля в поперечном сечении реальной ЛП совпадает со структурой поля в линии, имеющей идеально проводящие поверхности.
Из формул (3.80). (3.81) следует, что изменение мощности, проходящей через поперечное сечение ЛП на длине dl, dP = –2 mPdl. Это изменение равно по абсолютному значению и противоположно по
108

знаку мощности потерь в этом отрезке ЛП: dP=–Pmdl, где Рm — |
|
|||||
мощность потерь в металле на единицу длины линии (потери в |
|
|||||
диэлектрике не учитываем). Сопоставив эти выражения, |
найдем |
|
||||
м = Pm/(2P). |
|
|
|
(3.87) |
|
|
Мощность потерь в единице площади |
металлической |
Отформатировано: По ширине |
||||
поверхности определяется по закону Джоуля-Ленца: |
|
|
||||
p |
0.5R | J |
s |
|2 |
0.5R | H |2 . |
|
|
м |
s |
|
s |
|
|
|
Отсюда мощность потерь в отрезке линии единичной длины |
|
|||||
|
P 0.5R |
|
| H |2 dl, |
|
|
|
|
м |
s |
|
L |
|
|
где H — касательная к металлической поверхности составляющая
— касательная к металлической поверхности составляющая
 напряженности магнитного поля. Интегрирование здесь ведется по контуру всех металлических тел, образующих ЛП.
напряженности магнитного поля. Интегрирование здесь ведется по контуру всех металлических тел, образующих ЛП.
Подставив это значение в (3.87) и учитывая (3.79), запишем
Отформатировано: По ширине
|
|
|
|
|
|
|
Rs |
|
|
|
|
| H |2 |
dl |
|
|
|
|
(3.88) |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
L |
|
|
|
|
|
. |
|
|
|
|
|
|||
|
|
|
|
м |
|
2 Re Zc |
|
| H |2 dS |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
s |
|
|
|
|
|
|
|
|
|
|
|
|
Описанный метод расчета называется энергетическим. Он справедлив |
Отформатировано: По ширине |
||||||||||||||||||||||||
при условии, что поля в реальной ЛП и ЛП с идеально проводящими |
|
||||||||||||||||||||||||
поверхностями совпадают, что, |
|
в |
|
свою |
|
|
очередь, справедливо при |
|
|||||||||||||||||
m << . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
С учетом соотношений (3.45) – (3.48) |
выразим H |
и H через |
|
||||||||||||||||||||||
мембранную функцию. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Для поля Е- и Т-типа |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
H i |
|
|
e / n; |
H i |
|
|
|
|
|
ee |
; |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
e |
|
|
Rs |
k |
| |
e / |
|
n |2 |
dl |
|
|
(3.89) |
|
|||||||||||
|
|
|
|
L |
|
|
|
|
|
|
|
. |
|
|
|
||||||||||
|
м |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
2 Re Z0 |
|
|
|
| |
|
e |
|2 dS |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
S |
|
|
|
|
|
|
|
|
|
|
|
|
Для H-волн |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| H |2 | Hl |2 |
|
|
| Hz |2 |
|
|
|
2 | |
m / l |2 |
| k2 m |2 ; |
|
|
||||||||||||||
m |
Rs |
|
|
| |
|
m / l |2 |
|
k |
4 |
|
|
|
| m |2 dl |
(3.90) |
|
||||||||||
|
|
L |
|
|
|
|
|
|
|
|
|
|
L |
|
. |
|
|||||||||
м |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
||
2 Re Z0 k |
|
|
| |
|
m |2 dS |
|
|
| |
|
m |2 dS |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
S |
|
|
|
|
|
|
|
|
|
S |
|
|
|
|
|
|
|||
109

Из полученных выражений следует, что по мере приближения
 частоты к критической постоянная затухания всех типов волн неограниченно растет. При этом нарушается условие справедливости
частоты к критической постоянная затухания всех типов волн неограниченно растет. При этом нарушается условие справедливости
энергетического метода ( м << ), |
т. |
е. на частотах, очень близких к |
критической, записанные выражения теряют смысл. |
||
С увеличением частоты (k |
, |
k) постоянная затухания E- и |
T-волн увеличивается пропорционально росту Rs, т. е. пропорционально 1/2. Для H-волн при k = const первое слагаемое в (3.90), обусловленное поперечным магнитным полем (продольными токами в стенках линии передачи), также растет пропорционально 1/2, а второе слагаемое, обусловленное продольной
составляющей магнитного поля (поперечными токами в стенках), изменяется пропорционально отношению Rs/ 2, т. е. уменьшается пропорционально  . Это объясняется тем, что с увеличением частоты структура поля волны приближается к поперечной, и
. Это объясняется тем, что с увеличением частоты структура поля волны приближается к поперечной, и
отношение Hz /H быстро убывает. Если на |
металлических |
поверхностях линии передачи функция m постоянна ( |
m/ l), Hl = 0 и |
продольные токи в стенках отсутствуют. Вследствие этого затухание H-волны с фиксированным кс по мере роста частоты, как следует из формулы (3.90), неограниченно уменьшается.
На величину затухания в ЛП существенно влияет качество
 обработки поверхности металлических проводников. Если высота шероховатостей (микронеровностей) больше глубины проникновения
обработки поверхности металлических проводников. Если высота шероховатостей (микронеровностей) больше глубины проникновения
, путь поверхностного тока повторяет профиль микронеровностей, его путь удлиняется, и потери энергии возрастают. Так как глубина проникновения уменьшается с ростом частоты, требования к гладкости поверхности возрастают по мере увеличения частоты, на которой работает ЛП.
Участь влияние шероховатостей можно введением дополнительного множителя, учитывающего увеличение поверхностного сопротивления стенки:
Rs1 = krRs,
Отформатировано: По ширине
Отформатировано: По ширине,
Отступ: Первая строка: 1,27 см
Отформатировано: По ширине
110

где kr = 1 + k (K–1), k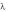 = th( /1.8 ) — частотный параметр, K —
= th( /1.8 ) — частотный параметр, K —
 коэффициент, учитывающий форму микронеровностей (для шлифованных поверхностей K 1.4), — средняя высота микронеровностей металлической поверхности.
коэффициент, учитывающий форму микронеровностей (для шлифованных поверхностей K 1.4), — средняя высота микронеровностей металлической поверхности.
Скорость уменьшения мощности по мере распространения волны принято характеризовать затуханием
A = 10lg(P2/P1),
где Р1, Р2 — потоки энергии в сечениях линии передачи, отстоящих
 друг от друга на единицу длины. В соответствии с формулой (3.80)
друг от друга на единицу длины. В соответствии с формулой (3.80)
A = 10lg(e2 ) = 8.68 Затухание измеряется в децибелах на единицу длины. Мощность P2 на выходе отрезка ЛП длиной l связана с мощностью на его входе P1 соотношением
Затухание измеряется в децибелах на единицу длины. Мощность P2 на выходе отрезка ЛП длиной l связана с мощностью на его входе P1 соотношением
P P 10 Al /10.
2 1
Контрольные вопросы
1.Какие признаки лежат в основе классификации направляющих систем и линий передачи.
2.Чем объясняется зависимость угла отражения плоской волны, распространяющейся между двумя параллельными идеально проводящими плоскостями, от частоты?
3.В чем заключается явление отсечки?
4.Поясните преимущества описания электромагнитного поля в регулярной ЛП с помощью векторов Герца.
5.Какие особенности имеют разделяющиеся системы координат? Приведите примеры таких систем.
6.Поясните, как используется метод разделения переменных для решения трехмерного скалярного уравнения Гельмгольца.
7.Каковы причины дисперсии волн в ЛП? Запишите дисперсионное уравнение волны в ЛП.
8.Какая связь существует между продольными составляющими электромагнитного поля волны и дисперсией?
9.Сформулируйте условия существования медленных волн в ЛП.
Отформатировано: По ширине
Отформатировано: По ширине
111
