
Лекция 3
.docЛекция №3. Механические колебания и волны
Колебания – это движение тела, в ходе которого оно многократно движется по одной и той же траектории и проходит при этом одни и те же точки пространства. Примерами колеблющихся объектов могут служить - маятник часов, струна скрипки или фортепиано, вибрации автомобиля. Колебания играют важную роль во многих физических явлениях за пределами области механики. Например, напряжение и сила тока в электрических цепях могут колебаться. Биологическими примерами колебаний могут служить сердечные сокращения, артериальный пульс и производство звука голосовыми связками. Хотя физическая природа колеблющихся систем может существенно отличаться, разнообразные типы колебаний могут быть охарактеризованы количественно сходным образом. Физическая величина, которая изменяется со временем при колебательном движении, называется смещением.Амплитуда представляет собой максимальное смещение колеблющегося объекта от положения равновесия. Полное колебание, или цикл – это движение, при котором тело, выведенное из положения равновесия на некоторую амплитуду, возвращается в это положение, отклоняется до максимального смещения в противоположную сторону и возвращается в свое первоначальное положение. Период колебания T – время, необходимое для осуществления одного полного цикла. Число колебаний за единицу времени - это частота колебаний.
Простое гармоническое колебание
В некоторых телах при их растяжении или сжатии возникают силы, противодействующие этим процессам. Эти силы прямо пропорциональны длине растяжения или сжатия. Таким свойством обладают пружины. Когда тело, подвешенное к пружине, отклоняют от положения равновесия, а потом отпускают, его движение представляет собой простое гармоническое колебание. Рассмотрим тело массой m, подвешенное на пружине в положении равновесия. Смещая тело вниз, можно вызвать колебание тела. Если - смещение тела от положения равновесия, то в пружине возникает сила F (сила упругости), направленная в противоположную смещению сторону. В соответствии с законом Гука, сила упругости пропорциональна смещению Fупр = -k·S , где k - константа, которая зависит от упругих свойств пружины. Сила является отрицательной, поскольку она стремится вернуть тело в положение равновесия. Действуя на тело массой m, сила упругости придает ему ускорение вдоль направления смещения. Согласно закону Ньютона F = ma, где a = d2S/d2t. Для упрощения последующих рассуждений пренебрежем трением и вязкостью в колеблющейся системе. В таком случае амплитуда колебаний не будет изменяться со временем. Если не действуют никакие внешние силы (даже сопротивление среды) на колеблющиеся тело, то колебания осуществляются с определенной частотой. Эти колебания называются свободными. Амплитуда таких колебаний остается постоянной. Таким образом, m·d2S/d2t = -k·S (1) . Перемещая все члены равенства и деля их на m, получим уравнения d2S/d2t +(k/m)·S = 0, а затем d2S/d2t +ω02·S = 0 (2), где k/m = ω02 Уравнение (2) является дифференциальным уравнением простого гармонического колебания. Решение уравнения (2) дает две функции: S = A sin(ω0t + φ0) (3) и S = A cos(ω0t + φ0) (4) Таким образом, если тело массой m осуществляет простые гармонические колебания, изменение смещения этого тела от точки равновесия во времени осуществляется по закону синуса или косинуса. (ω0t + φ0) - фаза колебания с начальной фазой φ0. Фаза является свойством колебательного движения, которое характеризует величину смещения тела в любой момент времени. Измеряется фаза в радианах. Величина называется угловой, или круговой, частотой. Измеряется в радианах, деленных за секунду ω0 = 2πν или ω0 = 2π/T (5) График уравнения простого гармонического колебания представлен на Рис. 1. Тело, первоначально смещенное на расстояние А – амплитуды колебания,а затем отпущенное, продолжает колеблется от -A и до A за время T - период колебания.
Р ис
1.
ис
1.
Таким образом, в ходе простого гармонического колебания величина смещения тела изменяется во времени вдоль синусоиды или косинусоиды. Поэтому простое гармоническое колебание часто называют синусоидальным колебанием. Простое гармоническое колебание имеет следующие основные характеристики: a) движущееся тело попеременно находится по обе стороны от положения равновесия; б) тело повторяет свое движение за определенный интервал времени; c) ускорение тела всегда пропорционально смещению и направлено противоположно ему; д) графически этот тип колебания описывает синусоида.
Затухающее колебание
Простое гармоническое колебание не может продолжаться сколь угодно долго при постоянной амплитуде. В реальных условиях через некоторое время гармонические колебания прекращаются. Такие гармонические колебания в реальных системах называются затухающим колебаниями (рис.2). К снижению амплитуды колебаний с последующим их прекращением приводит действие внешних сил, например, трения и вязкости. Эти силы уменьшают энергию колебаний. Они называются диссипативными силами, поскольку способствуют рассеиванию потенциальной и кинетической энергии макроскопических тел в энергию теплового движения атомов и молекул тела.
Р ис
2.
ис
2.
Величина диссипативных сил зависит от скорости тела. Если скорость ν сравнительно мала, то диссипативная сила F прямо пропорциональна этой скорости Fтр = -rν = -r·dS/dt (6) Здесь r - постоянный коэффициент, независимый от скорости или частоты колебаний. Знак минус указывает на то, что тормозящая сила направлена против вектора скорости движения. Принимаясь во внимание действие диссипативных сил, дифференциальное уравнение гармонического затухающего колебания имеет вид: m·d2S/d2t = -kS - r·dS/dt. Перенеся все члены равенства в одну сторону, разделив каждый член на m и заменяя k/m = ω2,r/m = 2β , получим дифференциальное уравнение свободных гармонических затухающих колебаний
|
|
где β - коэффициент затухания, характеризующий затухание колебаний за единицу времени. Решением уравнения является функция S = A0·e-βt ·sin(ωt + φ0) (8) Уравнение (8) показывает, что амплитуда гармонического колебания уменьшается экспоненциально во времени. Частота затухающих колебаний определяется уравнением ω = √(ω02 - β2) (9) Если колебание не может происходить вследствие большого , то система возвращается в свое положение равновесия по экспоненциальному пути без колебания.
Вынужденное колебание и резонанс
Если не сообщать колеблющейся системе внешнюю энергию, то амплитуда гармонического колебания уменьшается во времени из-за диссипативных эффектов. Периодическое действие силы может увеличить амплитуду колебаний. Теперь колебание не будет затухать со временем, поскольку потерянная энергия восполняется в течение каждого цикла действием внешней силы. Если будет достигнут баланс этих двух энергий, то амплитуда колебаний будет оставаться постоянной. Эффект зависит от соотношения частот вынуждающей силы ω и собственной частоты колебания системы ω0. Если тело колеблется под действием внешней периодической силы с частотой этой внешней силы, то колебание тела называется вынужденным. Энергия внешней силы оказывает наибольшее действие на колебания системы, если внешняя сила обладает определенной частотой. Эта частота должна быть такой же, как и частота собственных колебаний системы, которые бы эта система совершала в отсутствие внешних сил. В таком случае происходитрезонанс – явление резкого возрастания амплитуды колебаний при совпадении частоты вынуждающей силы с частотой собственных колебаний системы.
Механические волны
Распространение колебаний из одного места в другое называется волновым движением, или просто волной. Механические волны образуются вследствие простых гармонических колебаний частиц среды от их среднего положения. Вещество среды не перемещается при этом из одного места в другое. Но частицы среды, передающие друг другу энергию, необходимы для распространения механических волн. Таким образом, механическая волна является возмущением материальной среды, которое проходит эту среду с определенной скоростью, не изменяя своей формы. Если в воду бросить камень, от места возмущения среды побежит одиночная волна. Однако волны иногда могут быть периодическими. Например, вибрирующий камертон производит попеременные сжатия и разрежения окружающего его воздуха. Эти возмущения, воспринимаемые как звук, происходят периодически с частотой колебаний камертона. Существуют механические волны двух видов. (1) Поперечная волна. Этот вид волн характеризуется вибрацией частиц среды под прямым углом к направлению распространения волны. Поперечные механические волны могут возникать только в твердых веществах и на поверхности жидкостей. В поперечной волне все частицы среды осуществляют простое гармоническое колебание возле своих средних положений. Положение максимального смещения вверх называется "пиком", а положение максимального смещения вниз - "впадиной". Расстояние между двумя последующими пиками или впадинами называется длиной поперечной волны λ. (2) Продольная волна. Этот вид волн характеризуется колебаниями частиц среды вдоль направления распространения волны. Продольные волны могут распространяться в жидкостях, газах и твердых телах. В продольной волне все частицы среды также осуществляют простое гармоническое колебание около их среднего положения. В некоторых местах частицы среды расположены ближе, а в других местах - дальше, чем в нормальном состоянии. Места, где частицы расположены близко, называются областями сжатия, а места где они находятся далеко друг от друга - областями разрежения. Расстояние между двумя последовательными сжатиями или разрежениями называются длиной продольной волны. Выделяют следующие характеристики волн. (1) Амплитуда - максимальное смещение колеблющейся частицы среды от ее положения равновесия (A). (2) Период – время, необходимое частице для одного полного колебания (T). (3) Частота - количество колебаний, произведенных частицей среды, за единицу времени (ν). Между частотой волны и ее периодом существует обратная зависимость: ν = 1/T . (4) Фаза колеблющейся частицы в любой момент определяет ее положение и направление движения в данный момент. Фаза представляет собой часть длины волны или периода времени. (5) Скорость волны является скоростью распространения в пространстве пика волны (v). Совокупность частиц среды, колеблющихся в одинаковой фазе, формирует фронт волны. С этой точки зрения, волны делятся на два вида. (1) Если источник волны является точкой, из которой она распространяется во всех направлениях, то образуется сферическая волна. (2) Если источник волны колеблющаяся плоская поверхность, то образуется плоская волна. Смещение частиц плоской волны можно описать общим уравнением для всех типов волнового движения: S = A·sin ω · (t - x/v) (10) Это означает, что величина смещения (S) для каждой значения времени (t) и расстояния от источника волны (x) зависит от амплитуды колебания (A), угловой частоты (ω) и скорости волны (v).
Эффект Доплера
Эффект Доплера - изменение частоты волны, воспринимаемой наблюдателем (приемником) благодаря относительному движению источника волн и наблюдателя. Если источник волн приближается к наблюдателю, число волн, прибывающих к наблюдателю волн, каждую секунду превышает испускаемое источником волн. Если источник волн удаляется от наблюдателя, то число испускаемых волн больше, чем прибывающих к наблюдателю. Аналогичный эффект следует в случае, если наблюдатель перемещается относительно неподвижного источника. Примером эффекта Доплера является изменение частоты гудка поезда при его приближении и удалении от наблюдателя. Общее уравнение для эффекта Доплера имеет вид
|
|
Здесь νисточн - частота волн, испускаемых источником, и νприемн - частота волн, воспринятая наблюдателем. ν0 - скорость волн в неподвижной среде, νприемн и νисточн - скорости наблюдателя и источника волн соответственно. Верхние знаки в формуле относятся к случаю, когда источник и наблюдатель перемещаются друг к другу. Нижние знаки относятся к случаю удаления друг от друга источника и наблюдателя волн. Изменение частоты волн вследствие эффекта Доплера называют доплеровским сдвигом частоты. Этот феномен используется для измерения скорости перемещения различных тел, включая эритроциты в кровеносных сосудах.
|
Механические колебания
В
технике и окружающем нас мире часто
приходится сталкиваться с периодическими
(или почти периодическими) процессами,
которые повторяются через одинаковые
промежутки времени. Такие процессы
называют колебательными.К Механическими колебаниями называются движения тел, точно повторяющиеся через одинаковые промежутки времени. Закон движения тела, совершающего колебания, задается с помощью некоторой периодической функции времени x = f(t) (1). Графическое изображение этой функции дает наглядное представление о протекании колебательного процесса во времени. Примерами простых колебательных систем могут служить груз на пружине или математический маятник, изображенные на рисунке. |
|
Уравнение колебательного движения
Запишем
уравнение движения для случая
простейшего пружинного маятника,
расположенного горизонтально. Н
Пусть
сила трения пропорциональна
скорости, т.е.
Уравнение (3) – неоднородное линейное дифференциальное уравнение второго порядка, правая часть уравнения характеризует внешнее воздействие на систему.
При
отсутствии внешних сил (
и
в системе возникают свободные колебания.
При отсутствии трения уравнение
(4) упрощается:
В
этом случае полная механическая
энергия колебательной системы остается
постоянной, т.е. Решением уравнения (5) является функция вида x = xm cos (ωt> + φ0) (6). Здесь x – смещение тела от положения равновесия, xm – амплитуда колебаний, т. е. максимальное смещение от положения равновесия, ω – циклическая или круговая частота колебаний, t – время. Величина, стоящая под знаком косинуса φ = ωt + φ0 называется фазой гармонического процесса. При t = 0 φ = φ0, поэтому φ0 называют начальной фазой. |
|
Гармонические колебания Колебания, описываемые уравнением (6), являются гармоническими.
Минимальный
интервал времени, через который
происходит повторение движения тела,
называется периодом колебаний T.
Частота (величина, обратная периоду)
показывает, с На слева рисунке изображены положения тела через одинаковые промежутки времени при гармонических колебаниях. Такую картину можно получить экспериментально при освещении колеблющегося тела короткими периодическими вспышками света (стробоскопическое освещение). Интервал времени между последовательными положениями тела равен 1/12 периода. При колебательном движении тела вдоль прямой линии (ось OX) вектор скорости направлен всегда вдоль этой прямой.
Появление слагаемого + π/2 в аргументе косинуса означает изменение начальной фазы. Максимальные по модулю значения скорости vm = ω m достигаются в те моменты времени, когда тело проходит через положения равновесия (x = 0). Аналогичным образом определяется ускорение a тела при гармонических колебаниях:
На рисунке слева приведены графики координаты, скорости и ускорения тела, совершающего гармонические колебания.
Д
Таким
свойством обладает упругая сила в
пределах применимости закона Гука:
Круговую
частоту свободных колебаний ω0 груза
на пружине можно найти из уравнения (9): Частота ω0 называется собственной частотой колебательной системы. Все физические системы (не только механические), описываемые уравнением
способны совершать свободные гармонические колебания, так как решением этого уравнения являются гармонические функции вида (6). Уравнение (11) называется уравнением свободных колебаний. Следует обратить внимание на то, что физические свойства колебательной системы определяют только собственную частоту колебаний ω0 или период T. Такие параметры процесса колебаний, как амплитуда xm и начальная фаза φ0, определяются способом, с помощью которого система была выведена из состояния равновесия в начальный момент времени. |
|
Крутильный маятник
С Это соотношение выражает закон Гука для деформации кручения. Величина μ аналогична жесткости пружины k. Крутильный маятник широко используется в механических часах. Его называют балансиром. В балансире момент упругих сил создается с помощью спиралевидной пружинки. |
|
Затухающие колебания Рассмотрим колебания пружинного маятника, уравнение движения которого (согласно уравнению (4)) запишем в виде:
Первое слагаемое в данном уравнении характеризует силу трения, пропорциональную скорости маятника.
Введем
обозначения
Амплитуда и начальная фаза могут быть определены, если будут известны два значения смещения в произвольные моменты времени, т.е. так называемые начальные условия. Уравнение (14) описывает затухающие колебания.
Циклическая
частота затухающих колебаний
определяется выражением
Однако
во многих случаях, когда трение мало,
уменьшением частоты можно пренебречь,
и приближенно считать частоту свободных
колебаний равной частоте собственных
колебаний, т.е.
Характеристиками
затухающих колебаний являются
декремент затухания, определяемый из
условия
Наряду
с декрементом пользуются понятием
добротности
Затухающие
колебания происходят под действием
сил, характерных для колебательной
системы: силы упругости и силы трения.
Однако незатухающие колебания можно
получить с помощью внешних сил (см.
уравнение (3)).
Если внешняя сила периодична, то в
системе возникают колебания с частотой
изменения этой силы |
|
Механические волны Если в каком-нибудь месте твердой, жидкой или газообразной среды возбуждены колебания частиц, то вследствие взаимодействия атомов и молекул среды колебания начинают передаваться от одной точки к другой с конечной скоростью. Процесс распространения колебаний в среде называется волной. Механические волны бывают разных видов. Если при распространении волны частицы среды испытывают смещение в направлении, перпендикулярном направлению распространения, такая волна называется поперечной. Примером волны такого рода могут служить волны, бегущие по натянутому резиновому жгуту или по струне (рисунок слева). Если смещение частиц среды происходит в направлении распространения волны, такая волна называется продольной. Волны в упругом стержне (рисунок справа) или звуковые волны в газе являются примерами таких волн.
Механические волны могут распространяются в твердых, жидких и газообразных средах. Продольные механические волны могут распространяться в любых средах – твердых, жидких и газообразных. В жидкостях и газах упругая деформация сдвига не возникает. Если один слой жидкости или газа сместить на некоторое расстояние относительно соседнего слоя, то никаких касательных сил на границе между слоями не появляется. Силы, действующие на границе жидкости и твердого тела, а также силы между соседними слоями жидкости всегда направлены по нормали к границе – это силы давления. То же относится к газообразной среде. Следовательно, поперечные волны не могут существовать в жидкой или газообразной средах. Рассмотрим волну, которая распространяется в пространстве от источника, совершающего гармонические колебания. Если тело, являющееся источником колебаний, движется по закону y=ym cos (ωt) (20), то уравнение волны, распространяющейся от источника колебаний вдоль оси ОХ,будет иметь вид
где Длиной волны λ называют расстояние между двумя соседними точками на оси OX, колеблющимися в одинаковых фазах. Расстояние, равное длине волны λ, волна пробегает за период T, следовательно, λ = vT (23), где v – скорость распространения волны.
Обращаем
внимание, что волна, описываемая
уравнением (21),
движется вдоль оси ОХ, против
оси ОХ будет
двигаться волна, описываемая
уравнением
Скорость
распространения упругой волны зависит
от типа деформации и плотности среды,
и вычисляется как Например, при температуре 20 °С скорость распространения продольных волн в воде v ≈ 1480 м/с, в различных сортах стали v ≈ 5–6 км/с. |

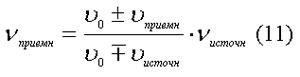
 олебательные
явления различной физической природы
подчиняются общим закономерностям.
Например, колебания тока в электрической
цепи и колебания математического
маятника могут описываться одинаковыми
уравнениями. Общность колебательных
закономерностей позволяет рассматривать
колебательные процессы различной
природы с единой точки зрения.
олебательные
явления различной физической природы
подчиняются общим закономерностям.
Например, колебания тока в электрической
цепи и колебания математического
маятника могут описываться одинаковыми
уравнениями. Общность колебательных
закономерностей позволяет рассматривать
колебательные процессы различной
природы с единой точки зрения.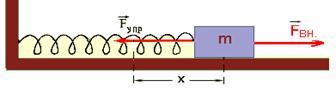 а
груз массой m, смещенный
из положения равновесия на расстояние
x, действует внешняя сила
а
груз массой m, смещенный
из положения равновесия на расстояние
x, действует внешняя сила 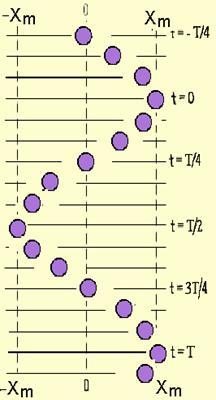 колько
колебаний совершается за единицу
времени:
колько
колебаний совершается за единицу
времени:  ля
того, чтобы свободные колебания
совершались по гармоническому закону,
необходимо, чтобы сила, стремящаяся
возвратить тело в положение равновесия,
была пропорциональна смещению тела
из положения равновесия и направлена
в сторону, противоположную смещению:
ля
того, чтобы свободные колебания
совершались по гармоническому закону,
необходимо, чтобы сила, стремящаяся
возвратить тело в положение равновесия,
была пропорциональна смещению тела
из положения равновесия и направлена
в сторону, противоположную смещению: или
или  (10).
(10). уществует
много разновидностей механических
колебательных систем, в которых
используются силы упругих деформаций.
На рисунке слева показан горизонтально
расположенный диск, висящий на упругой
нити, закрепленной в его центре масс.
При повороте диска на угол
уществует
много разновидностей механических
колебательных систем, в которых
используются силы упругих деформаций.
На рисунке слева показан горизонтально
расположенный диск, висящий на упругой
нити, закрепленной в его центре масс.
При повороте диска на угол 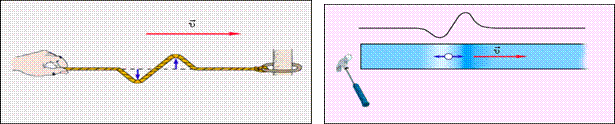 Волны
на поверхности жидкости имеют как
поперечную, так и продольную компоненты.
Волны
на поверхности жидкости имеют как
поперечную, так и продольную компоненты.