
fizika_dlja_flehshki_zaochniki / Final_1
.pdf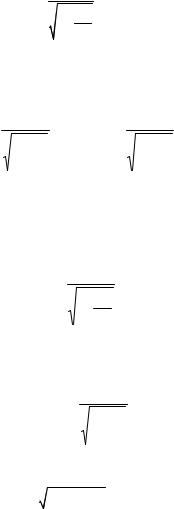
τ = τ0 , 1−Vc22
де τ0 – тривалість події для спостерігача, нерухомого відносно
об’єкта спостереження; τ– тривалість події для спостерігача, що рухається із швидкістю V .
29. |
Релятивістська маса, імпульс: |
|
G |
|
|
|
|
|
|||
|
m = |
m0 |
, |
G |
= |
m0υ |
, |
||||
|
|
V 2 |
p = mU |
|
|
V 2 |
|||||
|
1 |
− |
|
|
|
|
1 |
− |
|
||
|
c2 |
|
|
|
|
c2 |
|
||||
|
|
|
|
|
|
|
|
|
|
||
де |
m0 – маса спокою тіла; υ – швидкість руху в нерухомій системі |
||||||||||
відліку. |
|
|
|
|
|
|
|
|
|
|
|
30. |
Енергія спокою тіла: |
|
|
|
|
|
|
|
|
|
|
E0 = m0c2 .
Повна енергія в релятивістській механіці:
E = mc2 = m0c2 ,
1− V 2
c2
де m – релятивістська маса.
Кінетична енергія тіла в релятивістській механіці:
|
|
|
|
|
|
|
|
|
|
|
|
Wk = E − E0 |
|
1 |
|
|
|
= m0c |
|
|
2 |
−1 , |
|
|
|
1− |
V |
|
|
|
|
|
|
||
|
c2 |
||||
|
|
|
|
||
де E – повна енергія, E0 – енергія спокою тіла.
Релятивістське співвідношення між повною енергією та імпульсом:
E = p2c2 + E02 .
Механічні коливання і хвилі
31. Кінематичне рівняння гармонічного коливання матеріальної точки:
x(t) = Acos (ω0t +ϕ0 ) , ϕ(t) = ω0t +ϕ0 ,
29
де x(t) – зміщення частинки від положення рівноваги в момент часу t ; A – амплітуда коливань, ϕ(t) – фаза коливань; ϕ0 – початкова фаза коливань; ω0 – кутова швидкість або циклічна частота.
32.Швидкість та прискорення матеріальної точки, що виконує гармонічні коливання:
υ= −Aω0 sin(ω0t +ϕ0 ) , a = −A0ω02 cos (ω0t +ϕ0 ) = −ω02 x .
33.Диференціальне рівняння гармонічних коливань матеріальної
точки:
|
|
d 2 x |
+ω2 x = 0 , |
|
|||||||||||||
|
|
|
|
|
|
||||||||||||
|
|
dt2 |
0 |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
ω = |
|
|
k |
, |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|||||||||
|
|
0 |
|
|
m |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m – маса точки, k – |
|||
де ω0 – циклічна частота вільних коливань, |
|||||||||||||||||
коефіцієнт квазіпружної сили. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
34. Повна енергія |
матеріальної |
|
|
точки, що |
здійснює гармонічні |
||||||||||||
коливання: |
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
||||
|
E = |
mA2ω2 |
= |
kA2 . |
|
||||||||||||
|
|
2 |
|
2 |
|
||||||||||||
35. Періоди коливань маятників: |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
а) математичного |
|
|
T = 2π |
|
|
l |
; |
|
|
|
|||||||
|
|
|
|
g |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
б) пружного |
|
|
T = 2π |
|
|
m |
; |
|
|
||||||||
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
в) фізичного |
|
T = 2π |
|
|
Jz |
|
|
|
|
|
, |
|
|||||
|
|
mga |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||
де l – довжина математичного маятника; m – маса тіла; k – коефіцієнт пружності пружини; Jz – момент інерції тіла, що коливається;
a– відстань від центра мас до осі обертання.
36.Приведена довжина фізичного маятника:
lпр = maJz .
37. Амплітуда і початкова фаза результуючого коливання при складанні двох гармонічних коливань одного напрямку:
30
A = A2 |
+ A2 |
+2A A cos Δϕ |
0 |
; |
|
||
1 |
2 |
1 |
2 |
|
|
||
|
Δϕ0 = ϕ10 |
−ϕ20 ; |
|
|
|
||
tgϕ |
= |
A1 sin ϕ10 |
+ A2 sin ϕ20 |
. |
|||
|
|
||||||
0 |
|
A1 cos ϕ10 |
+ A2 cos ϕ20 |
||||
|
|
||||||
38. Рівняння траєкторії руху точки, перебуваючої одночасно у двох взаємно перпендикулярних коливаннях:
Ax22 + By22 −2 ABxy cos ϕ = sin2 ϕ , де x(t) = Acos ωt , y(t) = B cos (ωt +ϕ) .
39. Диференціальне рівняння загасаючих коливань: ddt22x + 2β dxdt +ω02 x = 0 ;
де β – коефіцієнт загасання, r – коефіцієнт опору, ω0 – циклічна частота вільних незгасаючих коливань, β = 2rm .
Розв’язок диференціального рівняння загасаючих коливань: x(t) = A0 e−βt cos (ωt +ϕ0 ) ,
де ω = ω02 −β2 , ω – частота загасаючих коливань.
Рівняння амплітуди загасаючих коливань:
A(t) = A0 e−βt .
Логарифмічний декремент загасання:
λ = ln |
A(t) |
= βT . |
|
A(t +T ) |
|||
|
|
40. Диференціальне рівняння вимушених коливань під дією періодичної зовнішньої сили:
ddt22x + 2β ddtϕ +ω02 x = Fm0 cos Ωt ,
де F0 – амплітуда періодичної сили, Ω – частота вимушуючої сили.
Частинний розв’язок диференціального рівняння вимушених коливань:
x(t) = Acos (Ωt −φ0 ) ,
де φ0 – зсув фази усталених коливань відносно вимушуючої сили. 41. Амплітуда вимушених коливань:
31

|
F |
|
|
A = m (ω02 −Ω20)2 + 4β 2Ω2 . |
|||
Зсув фази: |
2βΩ |
|
|
tgϕ0 = |
. |
||
ω2 −Ω2 |
|||
|
|
||
|
0 |
|
|
42.Резонансна частота і резонансна амплітуда:
ωрез = ω02 −2β2 ;
Aрез = |
|
F0 |
|
. |
2β |
ω2 |
|
||
|
−β2 |
|||
|
|
0 |
|
|
43. Зв’язок довжини хвилі з періодом і частотою коливань:
λ=υT = νυ .
44.Різниця фаз коливань двох точок середовища, в якому розповсюджується плоска хвиля:
Δϕ = 2λπ x ,
де x – найкоротша відстань між хвильовими поверхнями. 45. Рівняння стоячої хвилі:
ξ(x,t) = 2A0 cos kx cos ωt ,
де A = 2 A0 cos kx – амплітуда хвилі.
46. Швидкість поздовжньої хвилі в пружному середовищі:
υn =  Eρ ,
Eρ ,
де E – модуль Юнга, ρ – густина речовини. 47. Швидкість звуку в ідеальному газі:
|
|
υ = |
γ |
RT |
|
= γ |
p |
, |
|
|
|
|
M |
|
|
|
|
||||
|
|
|
|
|
|
ρ |
|
|
||
де γ = |
Cp |
– показник адіабати, |
|
R –універсальна газова стала, |
T |
– |
||||
C |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
υ |
|
M |
|
молярна маса, p – тиск газу, |
|
|
|||
термодинамічна температура, |
– |
ρ |
– |
|||||||
густина газу.
48. Середня об’ємна густина енергії пружної хвилі:
32

w = 12 ρξ02 = 12 ρω2 A2 ,
де ξ0 – амплітуда швидкості частинок середовища, ω – кругова
частота звукових хвиль.
49. Енергія звукового поля в об’ємі:
W = w V .
50. Потік звукової енергії:
Φ = Wt ,
де W – енергія, що переноситься через дану поверхню за проміжок часу t .
51. Інтенсивність звуку ( густина потоку енергії ):
I = w υ , G
де υ – швидкість звуку у середовищі; I – вектор Умова.
1.2 Приклади розв’язання задач.
Задача 1. Матеріальна точка рухається згідно рівнянням:
x = b t + d t3 , y = b t +c t2 , z = 0 , де b = 27 м/с; d |
1 |
= −1 м/с3; b = 32 м/с; |
||||||||
|
1 |
1 |
2 |
2 |
1 |
|
|
|
2 |
|
c |
= −8 м/с2. |
|
|
|
|
|
|
|
|
|
2 |
Знайти тангенціальне, нормальне прискорення та радіус кривизни |
|||||||||
|
||||||||||
траєкторії в момент часу t1 = 2 с. |
|
|
|
|
|
|
||||
|
|
|
|
Розв’язання |
|
|
|
|
||
|
За |
умовою |
задачі координата |
z = 0 , |
тобто рух |
відбувається в |
||||
площині xOy . |
|
|
|
|
|
|
|
|
||
|
Тангенціальне і нормальне прискорення можна знайти, якщо відомі |
|||||||||
модулі та напрямки векторів a та υ |
в заданий момент часу. Вектори a і |
|||||||||
υG |
можна знайти по їх проекціях на координатні осі. Проекції векторів a і |
|||||||||
υG |
можна одержати послідовним диференціюванням x(t) |
та y(t) : |
||||||||
|
|
|
|
aτ |
|
τ |
υ |
|
|
|
 n
n
a
 an
an
Рисунок 1.1
33

|
|
G |
|
dυ |
G |
|
G |
υ2 G |
|
||
|
|
aτ |
= |
|
τ , |
an = |
R |
n |
|
||
|
|
dt |
|
||||||||
де τG і nG – одиничні вектори (орти) спрямовані по дотичній і нормалі |
|||||||||||
до траєкторії відповідно. |
|
|
|
|
|
|
|
|
|
|
|
Проекції швидкості: |
|
|
|
|
|
|
|
|
|
||
υ |
x |
= b +3d t 2 , |
υ |
y |
= b + 2c |
2 |
t . |
||||
|
1 |
1 |
|
|
2 |
|
|
|
|||
Проекції прискорення:
ax = 6d1t , ay = 2c2 .
Вмомент часу t = 2c :
υx = 27 +3 4(−1) =15 (м/с),
υy = 32 −32 = 0 .
Отже, в момент часу t = 2 с вектор швидкості спрямовано по горизонталі υG =υx .
Прискорення в момент часу t = 2 с дорівнюють: ax = 6 (−1) 2 = −12 (м/с2), ay = 2 (−8)= −16 (м/с2).
Оскільки υy = 0 , то ax = aτ , |
ay = an . |
|
|
|
|
||||||
Таким чином, a = −12 м/с2, |
a |
n |
= −16 м/с2. |
|
|
||||||
|
τ |
|
|
|
|
|
|
|
|
|
|
Радіус кривизни R |
знаходиться |
із |
виразу |
для |
нормального |
||||||
прискорення: |
|
υ2 |
|
|
|
|
υ2 |
|
|
|
|
|
a = |
|
|
R = |
|
|
|
||||
|
|
|
=14 (м). |
|
|
||||||
|
n |
R |
|
|
|
|
an |
|
|
|
|
Задача 2. |
|
|
|
|
|
|
|
|
|||
Парашутист, |
маса |
|
якого |
m =100 кг, |
виконує затяжний |
||||||
стрибок. Його |
початкова швидкість υ0 = 0 . |
Знайти |
закон |
зміни його |
|||||||
швидкості до розкриття парашуту, якщо сила опору повітря пропорційна швидкості руху парашутиста: F0 = −kυG , де k = 20 кг/с.
Розв’язання
Парашутист починає рух із точки O . Вісь Ox спрямуємо вертикально вниз. На парашутиста діють дві сили: сила тяжіння mg та сила опору
повітря FGc = −kυG (рис 1.2).
34

o
h Fc
x
Рисунок 1.2
За другим законом Ньютона:
m ddtυ = mg −kυ
Звідки після розподілу змінних:
− |
|
dυ |
|
= |
k |
dt |
|
mg |
|
|
m |
||||
|
|
|
|
||||
|
|
k |
−υ |
|
|
|
|
|
|
|
|
|
|
|
|
|
mg |
|
|
|
||||
|
d |
|
|
−υ |
|
|||
|
|
|
|
|||||
або |
k |
|
|
|
= − |
k |
dt . |
|
mg |
−υ |
|
m |
|||||
|
|
|
|
|||||
|
|
k |
|
|
|
|
||
Після інтегрування одержуємо:
ln mgk −υ = − mk t +C .
Сталу C знаходимо з початкових умов (υ =υ0 = 0 при t = 0 ):
C= ln mg ,
k
|
mg |
|
|
k |
mg |
||||
тоді |
ln |
|
−υ |
= − |
|
t +ln |
|
|
|
k |
m |
k |
|||||||
|
|
|
|
|
|
||||
і закон зміни швидкості буде мати вигляд:
|
|
|
|
|
|
k |
|
|
|
mg |
|
|
|
− |
|
t |
|
|
|
|
||||||
υ = |
−e |
|
|
m |
||||
k |
1 |
|
|
|
|
. |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
При t → ∞ швидкість |
наближається до свого максимального |
|||||||
значення υmax = mg / k .
Задача 3. Потенціальна енергія частинки в центральному силовому полі задана рівнянням :
35
|
U (r) = |
A |
− |
B |
, |
|
r2 |
|
|||
|
|
|
r |
||
де A = 6 10−6 Дж·м2, |
B = 3 10−4 Дж·м, r – відстань від центра поля |
||||
до будь-якої точки поля. |
Знайти ті значення r , при яких потенціальна |
||||
енергія і сила, що діє на частинку, мають екстремальні значення; знайти ці
екстремальні значення; побудувати графіки залежності U (r) |
та Fr (r) , де |
||||||||||||
Fr – проекція вектора F на напрямок радіус-вектора r . |
|
||||||||||||
|
Розв’язання |
|
|||||||||||
Частинка знаходиться у потенціальному полі. Потенціальна енергія |
|||||||||||||
частинки в цьому полі – задана функція однієї координати |
r . Проекція |
||||||||||||
сили на напрямок радіус-вектора r : |
|
|
dU |
|
|
|
|
|
|||||
|
F = − |
. |
|
|
|
||||||||
|
|
|
|
|
|
||||||||
|
r |
|
|
|
dr |
|
|||||||
|
|
|
|
|
|
||||||||
Для заданої функції |
U (r) = |
|
A |
|
− |
B |
, |
|
|||||
|
r2 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
r |
|
|||||
|
F = 2 |
A |
− |
B |
. |
|
|||||||
|
|
|
|
|
|
|
|||||||
|
r |
r3 |
|
|
r2 |
|
|||||||
|
|
|
|
|
|||||||||
Оскільки A та B додатні величини, то перший член вiдповiдає силі відштовхування; другий – силі притягання.
Щоб знайти екстремальні значення потенціальної енергії, необхідно
знайти такі значення r , при яких перша похідна |
dU |
= 0 |
, тобто: |
||||||||||||||||||
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dr |
|
|
|
|
|
|
|
|
|
dU |
= −2 |
|
A |
+ |
B |
|
, |
|
|
|
||||
|
|
|
|
|
|
|
|
dr |
|
r2 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
r3 |
|
|
|
|
||||
|
|
|
−2 |
A |
+ |
B |
= |
1 |
|
(−2A + Br)= 0 . |
|
||||||||||
|
|
r2 |
r3 |
|
|||||||||||||||||
|
|
|
|
|
r3 |
|
|
|
|
|
|
|
|
|
|
|
|||||
Звідки |
|
|
|
|
|
|
|
|
|
dU |
|
= 0 , |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
dr |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
при r = r = |
2A |
= 4 10−2 |
м, U =U (r ) = −3,8 10−3 Дж. |
||||||||||||||||||
|
|
||||||||||||||||||||
1 |
B |
|
1 |
|
1 |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Очевидно, що |
dU |
> 0 при r не набагато більшим за r . |
|||||||||||||||||||
|
|||||||||||||||||||||
|
|
|
dr |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
U =Umin |
і при r = r1 дана |
|||||||
Отже, знайдене екстремальне значення |
|||||||||||||||||||||
частинка знаходиться в положенні рівноваги. |
|
|
|
|
|||||||||||||||||
При U (r) = 0 ( крім r → ∞ ): |
|
|
|
|
|
|
|
|
|
||||||||||||
36
|
|
|
|
|
|
A |
− |
B |
= 0 ; |
1 |
(A − Br )= |
0 , |
|
|
|
|||||||||||
|
|
|
|
|
|
r2 |
|
|
|
|
|
|
|
|
||||||||||||
|
|
A |
|
|
|
|
r |
|
|
|
r2 |
|
|
|
|
|
|
|
||||||||
при r = r |
= |
= 2 10−2 м; |
|
U (r ) = 0 . |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||
0 |
|
B |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
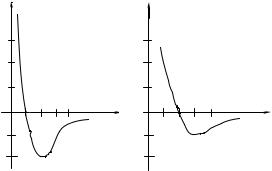
Графік U (r) |
наведений на рис. 1.3а. |
|
|
|
|
|
|
|||||||||||||||||||
Аналогічно для F (r) знайдемо такі r , при яких |
dFr |
= 0 ; |
||||||||||||||||||||||||
|
||||||||||||||||||||||||||
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dr |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dFr |
= − |
6A |
+ |
2B |
= |
2 |
(−3A + Br ), |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
r4 |
|
|
|||||||||||||||
|
|
|
|
|
dr |
|
|
|
r4 |
|
|
r3 |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
2 |
|
(−3A + Br)= 0 , |
|
|
|
|
|||||||||||
|
dFr |
|
|
|
|
|
|
r4 |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3A |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
r = r′ = |
|
−2 |
|
|
|||||||||
звідки |
|
|
= 0 |
|
|
при |
|
|
|
= 6 |
10 |
|
м. |
При цьому |
||||||||||||
dr |
|
|
|
|
|
B |
|
|||||||||||||||||||
Fr (r′) = −0,028 Н. Знак “-” показує, що при r = r′ |
на частинку діють сили. |
||||||
Значення r , при яких Fr |
= 0 , вже відомі; |
Fr = 0 |
при r → ∞ і при |
||||
r = r1 . Графік Fr (r) |
наведено на рис. 1.3б. |
|
|
|
|
||
U.1 0-3, |
|
|
F, H |
|
|
|
|
Дж |
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
4 |
|
0,05 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
0 2 4 6 8 |
r.1 0-2,H |
0 |
2 4 6 8 |
r.1 0-2,м |
|
||
-2 |
|
|
|
|
|
|
|
-4 |
|
-0,05 |
|
|
|
|
|
|
а) |
|
|
|
б) |
|
|
|
|
Рисунок 1.3 |
|
|
|
||
Задача 4. В однорідному диску |
, |
маса |
якого |
m =1 кг, |
радіус |
||
r = 30 см зроблено |
круглий |
отвір діаметром |
d = 20 см, центр |
якого |
|||
знаходиться на відстані l =15 см від осі диска. Знайти момент інерції J тіла відносно осі, яка проходить перпендикулярно площині диска через його центр.
37
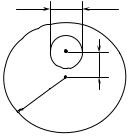
Розв’язання d
l
r O
Рисунок 1.4
Момент інерції тіла:
J = J0 − Jотв , |
(1) |
де J0 – момент інерції диска, якби він був заповнений речовиною; Jотв – момент інерції отвору.
Момент інерції отвору відносно осі диска знайдемо згідно з теоремою Штейнера:
|
|
Jотв = J ′+ mотв l2 , |
|
|
|
|
|
m r 2 |
|
|
|
d |
|
де J ′ = |
1 1 |
– момент інерції вирізаного диска радіусом |
r1 |
= |
|
|
2 |
2 |
|||||
|
|
|
|
відносно осі, що проходить через його центр мас; m1 ,r1 – маса і радіус цього диска.
Маси вирізаного диска та заданого відносяться як їх площини:
|
|
|
|
|
m |
|
= |
|
S |
; |
m |
= |
πr2 4 |
m = |
πd 2 |
m , |
|||||||||||||
|
|
|
|
|
m |
|
|
S |
|
m |
|
|
πd 2 |
|
|
|
1 |
|
4πr2 |
|
|||||||||
|
|
|
1 |
|
|
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
тобто |
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
= m = |
d 2 |
m . |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
отв |
|
|
1 |
|
|
4r2 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Момент інерції одержаного тіла дорівнюватиме: |
|
||||||||||||||||||||||||||||
|
mr |
2 |
|
|
d 2m d 2 |
|
d 2m |
|
|
|
|
mr |
2 |
|
d 2m |
|
|||||||||||||
J = |
|
|
|
|
− |
|
|
|
|
|
|
|
+ |
|
|
|
|
l2 |
|
= |
|
|
|
− |
|
|
(d 2 +8l2 )= |
||
|
2 |
|
|
|
|
2 |
2 |
|
|
|
|
2 |
|
2 |
|
32r |
2 |
||||||||||||
|
|
|
|
|
4r |
|
4 4r |
|
|
|
|
|
|
|
|
|
|
||||||||||||
= 4,19 10−2 кг м2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Задача 5. Маховик, маса якого |
m = 5 |
кг рівномірно розподілена по |
|||||||||||||||||||||||||||
ободу радіуса |
r = 20 |
|
см, |
вільно |
обертається |
з частотою n = 720 хв-1 |
|||||||||||||||||||||||
навколо горизонтальної осі, яка проходить через його центр інерції.
38
