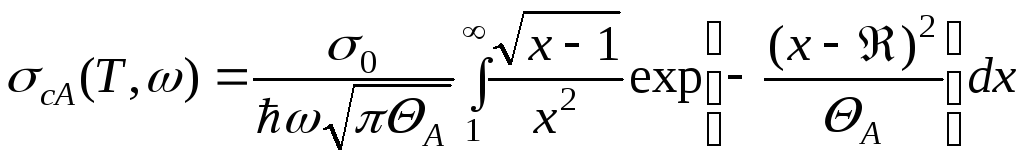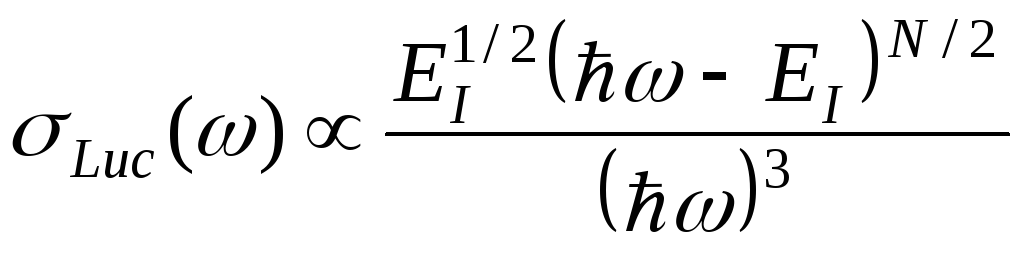3. О возможности прямого изучения локального электрон-фононного взаимодействия в полупроводниках
Локальное электрон-фононное взаимодействие в состояниях глубоких уровней дефектов полупроводников изучалось методами спектроскопии индуцированного поглощения света. На примере монокристаллов ZnS:Сu показано, что метод лазерной модуляции двухступенчатого примесного поглощения является эффективным инструментом для прямых исследований фононных релаксационных эффектов в состояниях глубоких дефектов. Показано, что локальные состояния в ZnS подвержены чрезвычайно сильной электрон-фононной связи.
Релаксация носителей в полупроводниках определяется, прежде всего, электрон-фононным взаимодействием (ЭФВ). С ростом степени локализации носителей сила ЭФВ резко возрастает, так как растет область перекрытия состояний носителей и фононов в k-пространстве волновых векторов. Известно, что спектры и эффективность излучательной рекомбинации существенно зависят от наличия и свойств глубоких локальных центров (ГЦ). Соответственно, явления локального ЭФВ в состояниях ГЦ имеют особое значение в формировании процессов безызлучательной рекомбинации.
Здесь мы сообщаем о прямом исследовании локального ЭФВ методами нелинейной спектроскопии ГЦ в широкозонных монокристаллах ZnS:Cu. Экспериментально показано, что метод лазерной модуляции двухступенчатого поглощения (ЛМДСП) является исключительно эффективным для прямого изучения процессов фононной релаксации локальных состояний глубоких дефектов. Получены основные параметры и построена модель конфигурационных координат для ГЦ в ZnS:Cu.
Выполнена теоретическая реконструкция полного спектра наблюдаемых ГЦ с применением лишь минимального набора их параметров. В результате удалось правильно описать не только энергии края оптических переходов, подверженные влиянию стоксовых потерь франк-кондоновского сдвига, но также и форму их длинноволнового поглощения, уширяемого электрон-фононным взаимодействием.
Ранее влияние локального ЭФВ обычно исследовалось косвенно, из температурных зависимостей уширения длинноволнового края спектров поглощения. Другой способ прямого изучения рассеяния свободных электронов фононами реализуется с использованием рамановской спектроскопии субпикосекундного разрешения.
Ч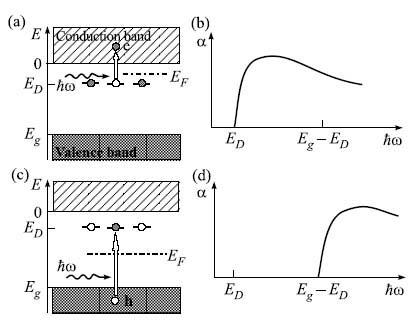 то
касается выбораZnS:Cu,
как объекта исследований, - это кристаллы,
открывшие начало изучения явлений
примесной люминесценции; двухступенчатые
процессы антистоксового возбуждения
ФЛ впервые наблюдались в них. Новейшие
нанотехнологии также не обошли этот
материал. Классический люминофор
оказывается затребованным в новых
разработках нано-полевых дисплеев и
световодных сенсоров.
то
касается выбораZnS:Cu,
как объекта исследований, - это кристаллы,
открывшие начало изучения явлений
примесной люминесценции; двухступенчатые
процессы антистоксового возбуждения
ФЛ впервые наблюдались в них. Новейшие
нанотехнологии также не обошли этот
материал. Классический люминофор
оказывается затребованным в новых
разработках нано-полевых дисплеев и
световодных сенсоров.
Для ГЦ характерным является
их проявление в спектроскопии поглощения
переходами лишь в одну из зон. Это либо
валентная, либо зона проводимости
(рис.1). Тип переходов (ионизация или
нейтрализация) определяется установившимся
заполнением ГЦ, или
Рис.1.
Схематическое представление формирования
спектров стационарного поглощения
глубокими центрами (ГЦ) с различной
степенью заселенности, то есть для
кристаллов с различным положением
уровня Ферми относительно состояний
ГЦ. (а), (Ь) Формирование спектров
фотоионизации Dc()
некомпенсированного
образца, (с), (d)
формирование
спектров фотонейтрализации D()
компенсированного
кристалла

Таким образом, традиционными методами стационарной спектроскопии практически невозможно исследовать полный спектр поглощения. Под словом "полный" имеем в виду возможность регистрации одновременно переходов как нейтрализации ("D") (рис.1b), так и ионизации ("D c") (рис.1а), так как они оба имеют место в отклике центров на их оптическую перезарядку.
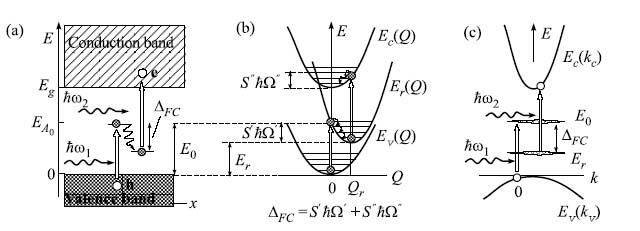
Во время оптической перезарядки локальных центров одновременно имеет место и релаксация решетки вблизи дефекта. Другими словами, локализованными носителями генерируются фононы. Это описывается правилом стоксовых потерь Франка-Кондона, которое иллюстрируется моделью диаграмм конфигурационных координат (рис.2b). При межзонном переходе через локальное состояние энергетические потери ES (затраты на образование фононов) равны ES=2FC, то есть двойному значению сдвига Франка-Кондона FC потому что фононы генерируются как на стадии локализации носителей, так и на стадии их освобождения (рис.2b).
 Таким
образом, мы хотели показать, что форма
полного спектра поглощения ГЦ
видоизменяется электрон-фононным
взаимодействием не только в виде уширения
длинноволнового края поглощения, но
также и коротковолновым сдвигом порогов.
При этом сумма пороговых энергий ED+EDc
будет больше ширины
запрещенной зоны Eg
на величину стоксовых
потерь ES=2FC.
Таким
образом, мы хотели показать, что форма
полного спектра поглощения ГЦ
видоизменяется электрон-фононным
взаимодействием не только в виде уширения
длинноволнового края поглощения, но
также и коротковолновым сдвигом порогов.
При этом сумма пороговых энергий ED+EDc
будет больше ширины
запрещенной зоны Eg
на величину стоксовых
потерь ES=2FC.
Определение стоксовых
потерь из измерений полного спектра
поглощения глубокими центрами и является
Рис.3.
Схема формирования спектра
фотоиндуцированного поглощения
для компенсированных ГЦ. (а), (b)
Проявление установившихся двухступенчатых
переходов, и (с) - их лазерной модуляции.
Здесь (d)
-спектр фотонейтрализации, а (е) - полный
спектр ДСП. Реакция двухступенчатых
переходов (b)
и их спектра (е) на дополнительную
модуляцию лазерным импульсом hL
показана
в форме изменения (f)
спектров
поглощения
и
как спектр (g)
индуцированного поглощения
Для измерения полного спектра ГЦ следует применять методы неравновесной спектроскопии, используя дополнительную импульсную подсветку. Это создает неравновесное частичное заполнение состояний дефекта. Рис.3 иллюстрирует формирование фотоиндуцированного спектра при наличии компенсированных ГЦ. Здесь рис.3а и 3b показывают появление двухступенчатых переходов, а рис.3с - их лазерную модуляцию. Здесь дана изначальная часть спектра фотонейтрализации (рис.3d) и полный спектр ДСП (рис.3е). Реакция двухступенчатых переходов (рис.3b) и их спектра (рис.3е) на дополнительную модуляцию лазерным импульсом ħL показана в виде изменений (рис.3f) спектров поглощения и (рис.3g) - спектра индуцированного поглощения .
Эксперименты проводились с использованием так называемого двухлучевого метода двухфотонной спектроскопии. В качестве зондирующего источника использовалась ксеноновая лампа (t 200 мкс) сплошного спектра, который монохроматизировался после прохождения через образец. Поглощение зондирующего света модулировалось импульсами рубинового лазера (ħL = 1.78 эВ, tL = 40нс). Экспериментальные результаты представлены на рис.4 и 5.
Идея метода определяется как ЛМДСП через глубокие уровни. Он дает возможность выделять спектральные вклады от разных ГЦ, используя различие их эффектов насыщения с ростом модуляции, даже в случае полного энергетического перекрытия их спектров. Определение основного набора феноменологических параметров и состава ГЦ также доступно.
Этот метод использовался ранее при исследовании и определении свойств ГЦ в кристаллах ZnTe, ZnSe, CdS и ZnO. Однако исследования (модуляция Nd3+-лазером с ħL = 1.17 эВ) были ограничены тем, что не было возможности регистрировать индуцированные сигналы с ħ<ħL, то есть в спектральной области, где могут наблюдаться пороги фотоионизации ГЦ. При использовании же рубинового лазера в данных материалах преобладало двухфотонное возбуждение кристалла и, соответственно, доминировала модуляция заселенности ГЦ захватом свободных носителей. В результате прямое изучение влияния ЭФВ реализовать на практике не удавалось.
Для более широкозонных кристаллов ZnS двухфотонное возбуждение отсутствует, так как ħL<Eg. Поэтому этот материал подходит для измерений полных спектров ЛМДСП и, соответственно, исследования локальной релаксации решетки при оптической перезарядке ГЦ.
Экспериментальные результаты рис.4 и 5 подтверждают, что индуцированное просветление с длинноволновой стороны спектров поглощения (рис.4) вместе с затянутой кинетикой сигналов и насыщающимися зависимостями от интенсивности (рис.5) являются типичными проявлениями ЛМДСП.
Как обычно, спектры (рис.4) сложны, образуясь из перекрытия сигналов индуцированного просветления и поглощения от каждого вида центров. Спектральные зависимости соответствуют комбинации спектров сечений фотоионизации и фотонейтрализации в форме [cA()A()] (см. рис.3g). Модуляция ДСП происходит вследствие изменения заселенности ГЦ прямым поглощением лазерного излучения с ħL > Ei примесным центром, как показано на рис.3c.
|
Параметры центров |
1 |
2 |
|
Сечение фотоионизации (A(L), см2) |
0.6310-17 |
0.47510-18 |
|
Времена жизни локализованных дырок (, мкс) |
1.2 |
0.5 |
|
Энергия связи дырок (EA, эВ) |
1.415 |
1.65 |
|
Край фотонейтрализации (EcA, эВ) |
2.83 |
2.67 |
|
Стоксовые потери Франка-Кондона (FC, эВ) |
0.515 |
0.59 |
|
Константа электрон-фононного взаимодействия (aA) |
6.55 |
7.0 |
Анализ насыщающихся
зависимостей (IL)
индуцированных сигналов от интенсивности
модулирующего лазерного излучения
позволяет определить абсолютные значения
сечений фотоионизации поглощения
лазерных квантов A
(см. таблицу). На рис.5 представлены
экспериментальные зависимости (IL)
для двух спектральных областей
фотоиндуцированного поглощения и
соответствующие теоретические
кривые. Как видим, сигналы с энергией
квантов выше 2.1 эВ
формируются обоими центрами, а ниже
2 эВ,
- только более глубоким ГЦ, что
позволяет у
Рис.5.
Зависимости амплитуды сигналов
индуцированного примесного поглощения
в ZnS:Cu
от интенсивности оптической модуляции,
измеренные при: ħ
= 2.1
и 2.5эВ.
Кривые 1
и
2
- рассчитанные
зависимости. Причем, 2
получена
в предположении, что зависимость при
2.5
эВ
обусловлена перекрытием сигналов от
обоих ГЦ (1+2)
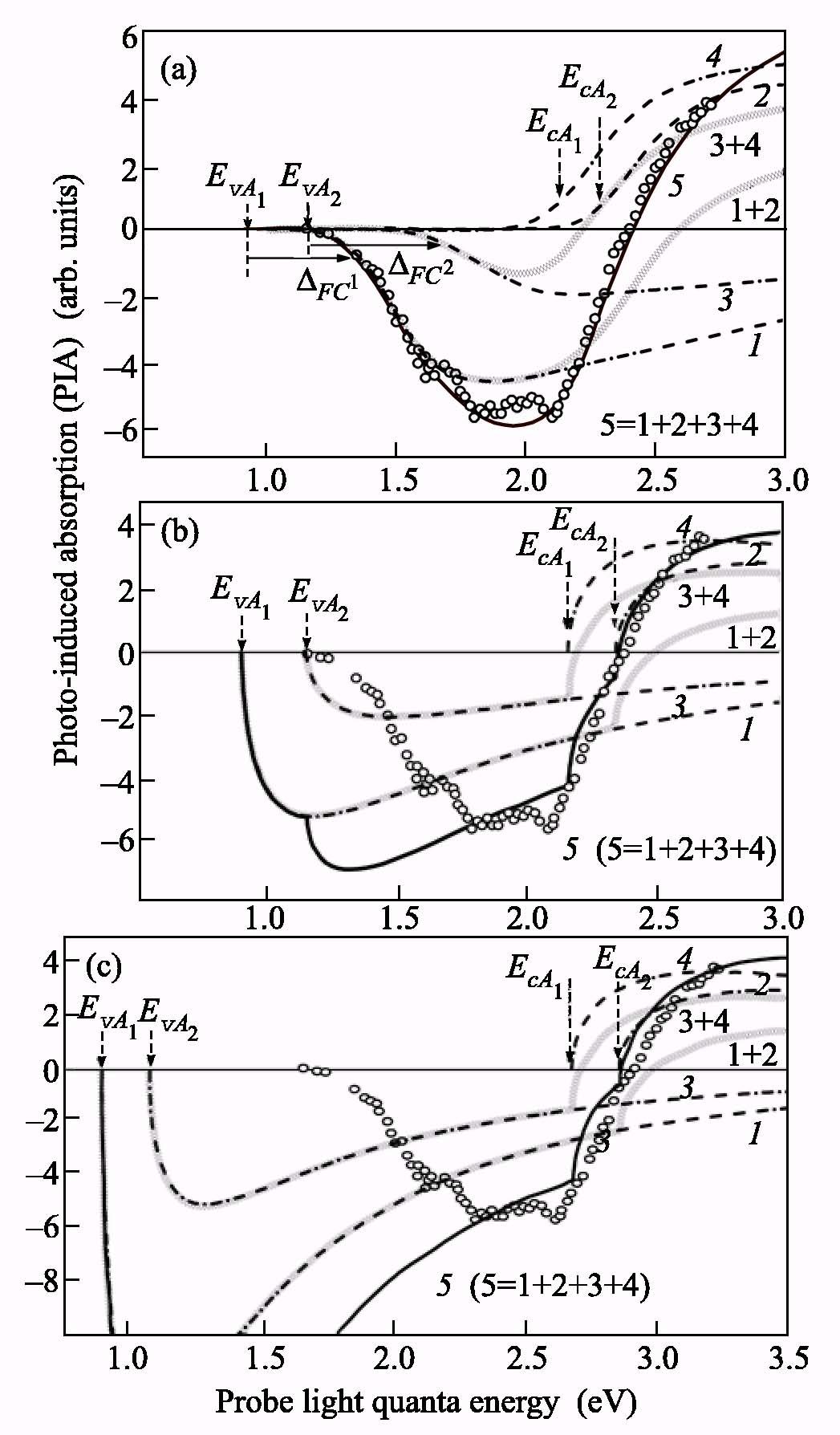
Рис.4.
Сравнение экспериментального спектра
фотоиндуцированного поглощения в
ZnS:Cu
при 300 К (точки), формируемого процессами
ЛМДСП, с рассчитанными спектрами в виде
комбинации Ac()-A()
спектров
фотоионизации A()
и
фотонейтрализации Ac()
двух
глубоких акцепторов с EcA
=
2.67
эВ и 2.83эВ. Представлены спектры для:
(а) переходов, подверженных фононной
релаксации, согласно формулам (1)-(3);
(b),
(с) те же самые ГЦ в жесткой решетке, в
модели Луковского согласно (4), для
состояний со стоксовым сдвигом (b),
когда EA+EAc+FC
= Eg,
и
для случая нерелаксированных
состояний (с) с EA+EAc
= Eg
Компоненты,
формирующие спектр оптическими
переходами A
(1 и
3) и Ac
(2 и
4) показаны отдельно, а также в форме их
естественной комбинации. Кривая 5 -
расчетные спектры результирующего
ЛМДСП.
Рис.4.
Сравнение экспериментального спектра
фотоиндуцированного поглощения в
ZnS:Cu
при 300
К
(точки), формируемого процессами ЛМДСП,
с рассчитанными спектрами в виде
комбинации Ac()-A()
спектров
фотоионизации A()
и
фотонейтрализации Ac()
двух
глубоких акцепторов с EcA
=
2.67
эВ и
2.83эВ.
Представлены спектры для: (а) переходов,
подверженных фононной релаксации,
согласно формулам (1)-(3); (b),
(с) те же самые ГЦ в жесткой решетке, в
модели Луковского согласно (4), для
состояний со стоксовым сдвигом (b),
когда EA+EAc+FC
= Eg,
и
для случая нерелаксированных
состояний (с) с EA+EAc
= Eg
Компоненты,
формирующие спектр оптическими
переходами A
(1 и
3) и Ac
(2 и
4) показаны отдельно, а также в форме их
естественной комбинации. Кривая 5 -
расчетные спектры результирующего
ЛМДСП.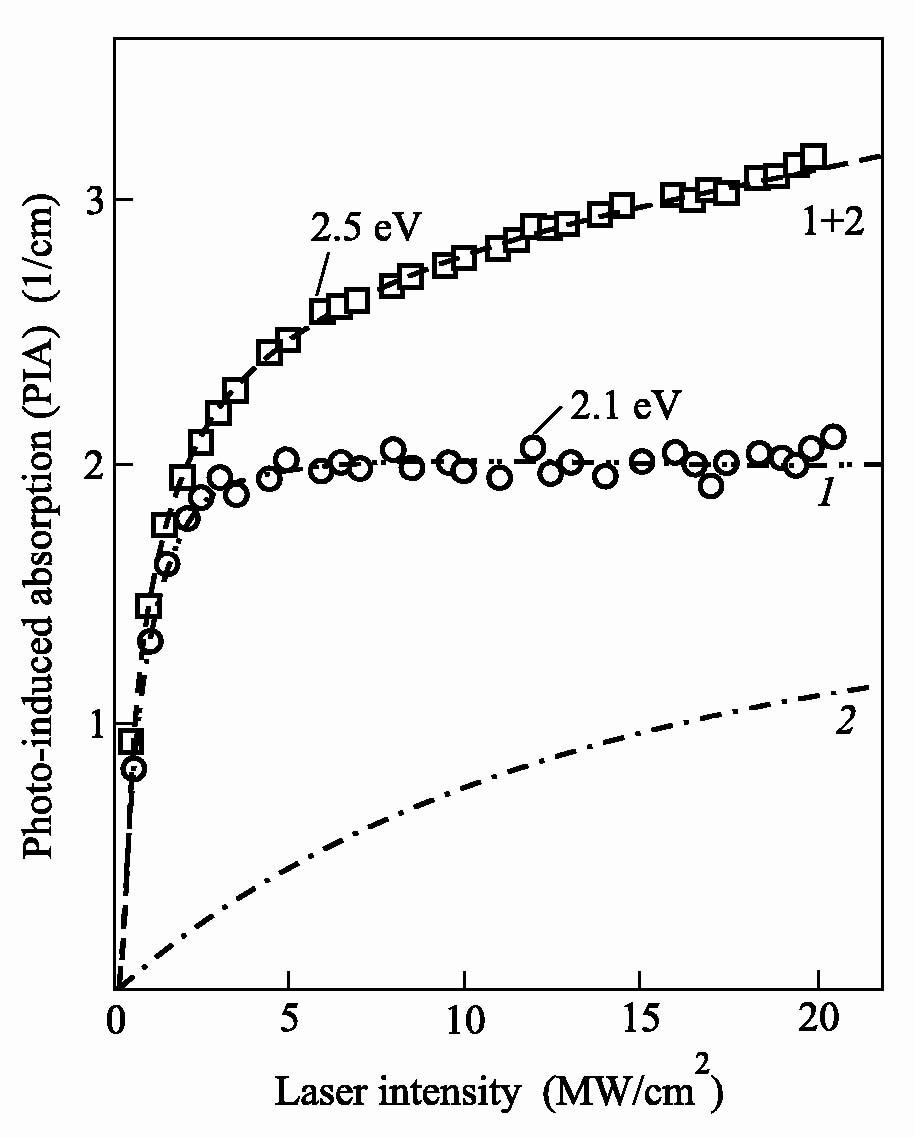 веренно
разделить их вклады в полный спектр.
веренно
разделить их вклады в полный спектр.
 спектра
и их интенсивные зависимости
сформированы главным о
спектра
и их интенсивные зависимости
сформированы главным о
В нашем случае край спектра существенно размазан, следовательно, возможно влияние фононов в формировании спектров. Удовлетворительное описание спектров ЛМДСП может быть выполнено в рамках модели -потенциала с учетом электрон-фононного взаимодействия. Теоретический спектр сечения фотонейтрализации и его температурные изменения можно получить следующим образом:
|
|
(3.1) |
Здесь A имеет смысл параметра сглаживания спектров из-за ЭФВ:
|
|
(3.2) |
aA безразмерная константа ЭФВ, ħ - энергия локальных колебаний решетки, ħ - энергия фотона;
|
|
(3.3) |
Для спектров фотоионизации получим подобное (1) выражение, но с другими =EA и = =ħ•EA-1. Выражение (3.1) может быть сравнено со спектром в простом приближении -потенциала Луковского для глубоких центров в "жесткой" решетке:
|
|
(3.4) |
Здесь N = 1 для разрешенных переходов и N = 3 для запрещенных переходов. ЕI энергия ионизации ГЦ.
Сравнение экспериментального
спектра (точки) и теоретических вычислений
представлено на рис.4. Кривая 5
на рис.4а - спектр с
полным учетом электрон-фононного
взаимодействия (3.1) для двух центров
с еcA
= 2.67
и
2.83 эВ. Кривые же на
рис.4Ь и 4с показываются для сравнения
и соответствуют случаю тех же центров,
но для гипотетической "жесткой"
решетки Луковского (4). Компоненты,
формирующие спектр посредством
оптических переходов A
 (1
и 3)
и Ac
(2 и
4)
показаны отдельно, а
также в форме их естественных комбинаций
1+2 и
3+4.
Кривые 5
- спектры результирующей
ЛМДСП согласно выражениям (3.1)-(3.3).
(1
и 3)
и Ac
(2 и
4)
показаны отдельно, а
также в форме их естественных комбинаций
1+2 и
3+4.
Кривые 5
- спектры результирующей
ЛМДСП согласно выражениям (3.1)-(3.3).
Спектры типа Луковского (4), представленные на рис.4b и 4c, отличаются включением эффекта стоксовых потерь (b), когда EA+EAc+FC = Eg. Кривые рис.4с соответствуют простым нерелаксированным состояниям с EA+EAc = Eg. Различия в расчетных спектрах на рис.4 демонстрируют, насколько сильно может быть влияние ЭФВ на формирование спектров ГЦ в широкозонных полупроводниках. Так, не учитывая ЭФВ, имеем ошибку в оценке энергии связи центра порядка FC 0.5-0.6 эВ, а при описании формулой Луковского (3.4), - вплоть до 1эВ и более.
П
Рис.6.
Модель конфигурационных координат для
исследованных глубоких центров в
линейной аппроксимации
Эти вычисления формируют базис для модели конфигурационных координат ГЦ (рис.6), которая может быть использована для определения энергии невозмущенных состояний Em и соответствующих стоксовых потерь FC из-за релаксации решетки при оптической перезарядке. Эти параметры и константа ЭФВ aA были получены (см. таблицу) при предположении, что энергия локальных колебаний ħLO равна ЗЗ мэВ.
Итак, преимущества нелинейной спектроскопии позволяют наблюдать полные спектры глубоких локальных центров в кристаллах, то есть регистрировать одновременно взаимосвязанные спектры, как фотоионизации, так и фотонейтрализации.
Наиболее важный результат - то, что непосредственно исследовано локальное электрон-фононное взаимодействие в кристаллах. Полученная информация позволила сделать теоретическую реконструкцию полного экспериментального спектра с использованием лишь минимального набора параметров. Далее, с использованием тех же параметров энергии связи ГЦ и силы электрон-фононного взаимодействия были описаны не только края оптических переходов, сдвинутых стоксовыми потерями, но также и форма длинноволнового края поглощения, уширенного электрон-фононным взаимодействием. Результаты показывают, что для глубоких локальных состояний в широкозонных кристаллах типа ZnS характерны чрезвычайно сильные эффекты электрон-фононной связи.