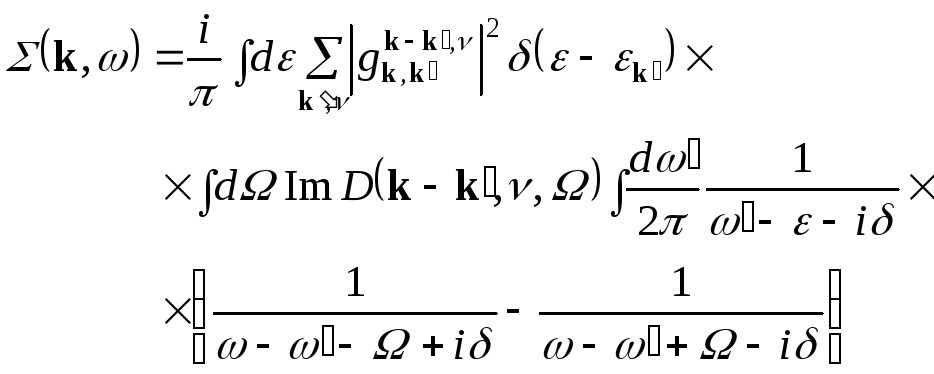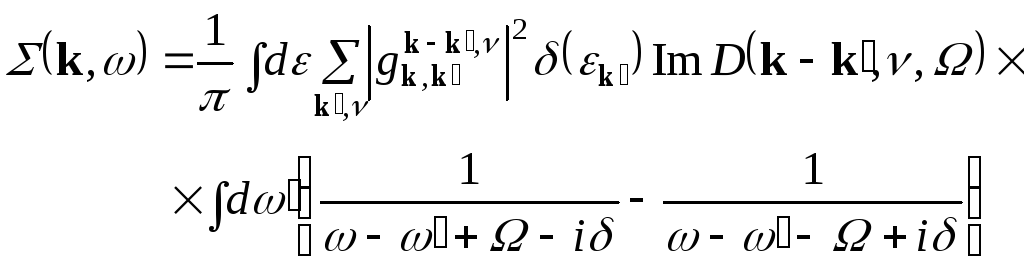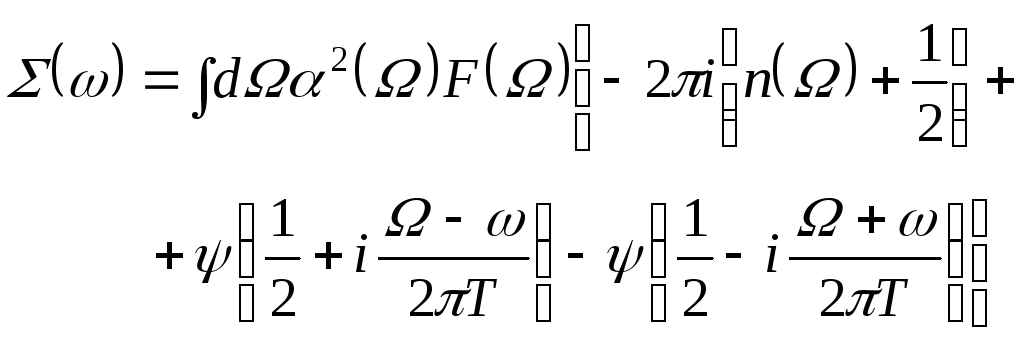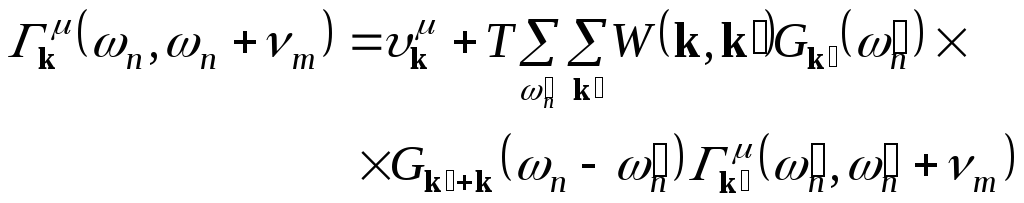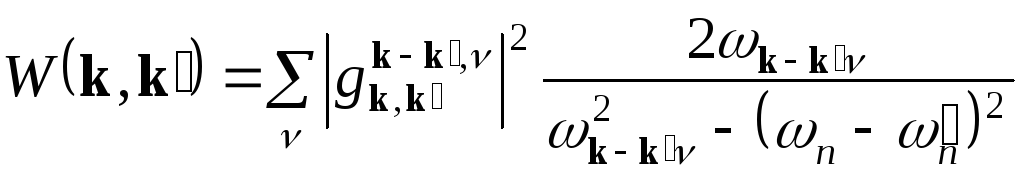2. Многочастичная теория электрон-фононного взаимодействия

Многочастичная теория ЭФВ изложена в большом количестве обзоров и книг, и мы не будем здесь останав­ливаться на ее подробном рассмотрении. Приведем лишь основные факты этой теории, а также формулы, которые будут использованы в дальнейших разделах этого обзора. Прежде всего, отметим, что в многочастич­ной теории для описания ЭВФ обычно используется так называемый гамильтониан Фрелиха

(2.1)

Здесь Н_е описывает квазистационарные состояния элект­ронов в жесткой решетке:

(2.2)

где H_e — энергия электронных квазичастиц, c⁺_k и c_k операторы рождения и уничтожения квазичастиц; гамильтониан невзаимодействующих фононов:

(2.3)

при этом _k — энергия фонона с поляризацией , a b⁺_q и b_q, — соответствующие фононные операторы; H_e-ph представляет собой гамильтониан электрон-фононного взаимодействия:

(2.4)

где g^q_k+q,k — матричный элемент ЭФВ. Позднее мы возвратимся к более подробному обсуждению возмож­ности использования гамильтониана Фрелиха для опи­сания ЭФВ и расчета входящих в него функций, таких как электронные и фононные энергии и матричный элемент ЭФВ.

В данный момент мы перейдем к изложению резуль­татов расчетов ЭФВ в рамках гамильтониана Фрелиха. Для соответствующих расчетов в многочастичной тео­рии ЭФВ используется обычно метод функций Грина. В задачи нашего обзора не входит изложение этого метода. Впервые расчеты ЭФВ с использованием функций Грина были проведены Мигдалом для нормального состояния металла и Элиашбергом для сверхпроводящего состояния. Наше рассмотрение мы начнем со случая температур Т = 0, поскольку при этом все соответствую­щие формулы выглядят гораздо проще и позволяют легко ввести определение необходимых для дальней­шего спектральных функций ЭФВ. Электронная функ­ция Грина G(k,) и фононная функция Грина D(q,,) могут быть записаны с помощью электронной (k,) и фононной (q,,) собственно-энергетических частей в виде

	(2.5)
	(2.6)

Здесь G₀(k,) — функция Грина невзаимодействующих электронов, определяемая гамильтонианом H_e:

(2.7)

Функция D₀(q,,) определяется гамильтонианом H_ph и имеет вид

(2.8)

Забегая вперед, отметим, что в общем случае само­согласованное вычисление функций Грина электронов и фононов в рамках гамильтониана Фрелиха не может быть строго обосновано. Точная функция D(q,,)должна вычисляться в рамках полного электрон-ионного гамильтониана. Для целого ряда задач, однако, гамиль­тониан Фрелиха можно использовать и для самосогла­сованного вычисления обеих функций Грина, определив соответствующим образом, затравочные фононы в функ­ции D₀(q,,). В любом случае затухание фононов, определяемое мнимой частью собственной энергии фононов (q,,), дается правильно в рамках этого гамильтониана. В дальнейшем мы не будем в этом обзоре обсуждать расчеты фононной функции Грина, считая, что во всех формулах, описывающих электронные свойства, определяемые ЭФВ, нужно ис­пользовать точные функции Грина фононов.

Один из основных результатов работы Мигдала состоит в том, что электронная собственно-энергетиче­ская часть может быть вычислена с учетом простейших вкладов первого порядка по ЭФВ, а слагаемыми более высокого порядка можно пренебречь, поскольку они малы в отношении _D/_F. Здесь _D — характерная фононная частота и _F — энергия Ферми. В аналитиче­ском виде выражение для (k,) можно записать как

(2.9)

Для дальнейшего удобно воспользоваться спектраль­ным представлением фононной функции D(q,,):

(2.10)

В адиабатическом приближении и без учета взаимодей­ствия фононов друг с другом Im(D(q,,)) имеет вид

(2.11)

Удобно также представить суммирование по векторам k в виде

(2.12)

Используя введенные обозначения, можно переписать выражение для (k,):

(2.13)

Можно убедиться исходя из формулы (2.13), что (k,) по абсолютной величине ~_D. Из этого следует, как было показано Мигдалом, что электронная функция Грина в выражении (2.13) может быть заменена на функцию Грина невзаимодействующих электронов G₀(k,). В результате (2.13) приобретает вид

(2.14)

Из анализа выражения (2.14), проведенного Мигдалом, следует, что существенные значения величин  и ' порядка _D. Это означает, что и для величины  сущест­венны тоже малые значения ~_D. В этом случае в величине (-_k) можно пренебречь . После этого интеграл по  берется тривиально, и окончательно для (k,) имеем

(2.15)

Вводя спектральную плотность ЭФВ _k²()F(), равную

(2.16)

выражение для (k,) получим в виде

(2.17)

Здесь

(2.18)

Заметим сразу, что в силу принятых приближений, а они верны при условии _D<<_F, функция (k,) зависит лишь от угловой части вектора k, лежащего на поверхно­сти Ферми. Интеграл (2.18) для функции L(,) может быть легко вычислен, но мы не будем этого делать здесь. Можно показать, что выражение для собственной энергии (k,) имеет в точности такой же вид, как и формула (17), и при любой температуре. Выражение для функции L(,) при T 0 записывается как

(2.19)

где (x) — дигамма-функция, n() — функция распреде­ления Бозе. Можно определить функцию (), дающую усредненное значение собственно-энергетической части по поверхности Ферми:

(2.20)

где N(_F) — плотность состояний электронов на поверх­ности Ферми;

(2.21)

Введенная выше функция _k²()F() называется обычно спектральной плотностью ЭФВ или функцией Элиашберга и имеет вид

(2.22)

Эта функция определяет, в частности, сверхпроводящие свойства металлов.

Как мы уже отмечали ранее, хотя гамильтониан Фрелиха в общем случае не пригоден для расчета точных фононных спектров, затухание фононов может быть вычислено в его рамках. С этой целью необходимо вычислить мнимую часть собственной энергии фононов (q,,). Подобные расчеты были проведены Алленом, где было показано, что затухание фононов _q с данной энергией _q есть

(2.23)

Сравнивая формулы (2.22) и (2.23), видим, что функция Элиашберга может быть выражена через величины затухания фононов следующим образом:

(2.24)

Собственно-энергетическая часть () имеет дей­ствительную и мнимую части и может быть предста­влена в виде

(2.25)

Как известно, функция (,Т) характеризует перенормировку массы электронов за счет ЭФВ, и (,Т) характеризует время жизни электрона. В этом легко убедиться, переписывая выражение для функции Грина в виде

(2.26)

где введено обозначение

(2.27)

Здесь m – масса невзаимодействующих зонных электронов. При T=0 и =0 величина (,Т) представляет собой константу электрон-фононной связи

(2.28)

Энергия квазичастицы определяется полюсом функции Грина, и мы имеем

(2.29)

где . Естественно, что хорошо определенные квазичастицы существуют лишь при условии

(2.30)

Это неравенство в металлах нарушается в довольно широком интервале энергий вблизи поверхности Ферми. Само же по себе выражение (2.26) для функции Грина электронов имеет гораздо большую область применимости в системах с ЭФВ и остается справедливым при наличии лишь малого параметра _D/_F. Мнимая часть функции Грина может быть непосредственно измерена в экспериментах по фотоэмиссии с угловым разрешением.

С использованием гамильтониана Фрелиха может быть вычислена и электропроводность () металлов, обусловленная ЭФВ. С этой целью не­обходимо вычислить электромагнитное ядро K_()=4_()/, где =x, y, z. В металлах с кубической решеткой, этот тензор сводится к скаляру K(). В технике температурных функций Грина K() дается следующим выражением:

(2.31)

Здесь _n=2Tmи _n=T(2n+1), _k^ — компоненты электронной скорости, Г_k^(_n,_n+_m) — вершинная функция. Для вершинной функции, в свою очередь, можно написать интегральное уравнение

(2.32)

Здесь W(k,k) — электрон-фононное взаимодействие:

(2.33)

Уравнение для вершинной функции Г_k^(_n, _n+_m) можно решить вариационным методом, выбирая для Г_k^(_n, _n+_m) пробную функцию в виде

(2.34)

Учитывая, как и при рассмотрении одночастичной функции Грина, что ЭФВ локализовано вблизи поверхности Ферми, где все остальные величины за исключением одночастичной функции Грина меняются слабо, можно получить окончательный ответ для проводимости () в виде, очень напоминающем одночастичную функциюГрина:

(2.35)

Функция _tr() по аналогии с собственно-энергетической частью. () также может быть выражена через пере­нормированную массу и время релаксации:

(2.36)

Выражения для транспортных перенормированной массы и времени релаксации, вообще говоря, отли­чаются от даваемых формулой (21). Впервые для Т=0 формулы для

и

были получены Алленом. Позднее они были об­общены на случай конечных температур. В общем случае эти формулы имеют вид

(2.37)

где

(2.38)

При описании процессов переноса и, в частности, оптиче­ской проводимости появляется еще одна спектральная плотность ЭФВ _tr²()F(), которая может быть пред­ставлена в виде

(2.39)

где

(2.40)

Здесь _x² — усредненный квадрат скорости электрона на поверхности Ферми. Эта величина непосредственно связана с плазменной энергией _p, входящей в опреде­ление оптической проводимости:

(2.41)

В заключении этого раздела мы приведем для справки без всякого вывода уравнения Элиашберга, описывающие сверхпроводящие свойства металлов. Эти уравнения включают две функции: параметр порядка () и функцию перенормировки Z(). В нормальном состоянии величина (), естественно, равна нулю, а функция перенормировки Z() переходит в ранее введенную функцию перенормировки массы Z^N(,T)=m*(,T)/m

	(2.42)
	(2.43)

Здесь f() — фермиевская функция распределения, (_F) — усредненное кулоновское межэлектронное взаи­модействие. К сожалению, до настоящего времени отсутствуют какие-либо разумные методы расчета вели­чины (_F), и чаще всего (_F) рассматривается как некоторая феноменологическая постоянная.