§ 29. Поперечные электромагнитные волны в незамагниченной плазме.

Вооружившись полученными в предыдущем параграфе результатами, рассмотрим процесс распространения электромагнитных волн в плазме. Как мы уже знаем (см. § 27), задача сводится к решению дисперсионных уравнений

,

или

в зависимости от того, какой конкретно тип волны нас интересует: чисто продольные или чисто поперечные волны. Последний случай особенно прост. С него и начнем обсуждение плазменных волн.

П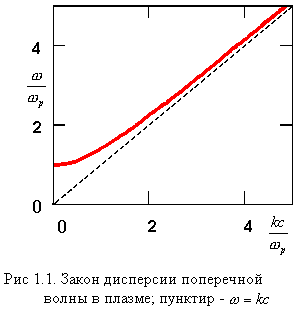оскольку для поперечных волн диэлектрическую проницаемость плазмы определяет соотношение (4.33), то дисперсионное уравнение будет таким:

.

Решением этого уравнения, очевидно, является

.

Это соотношение и определяет закон дисперсии поперечной волны в плазме (рис.1.1). Обратим внимание, что для коротких волн, когда , получаем , так что в этом пределе волна (4.36) становится обычной световой волной. Для длинных волн, когда , приближенно

.

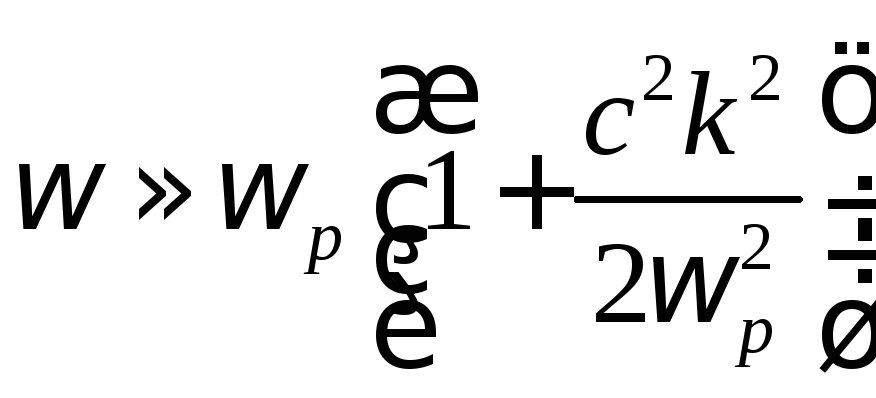Заметим также, что для фазовой скорости волны закон дисперсии (4.36) дает значение

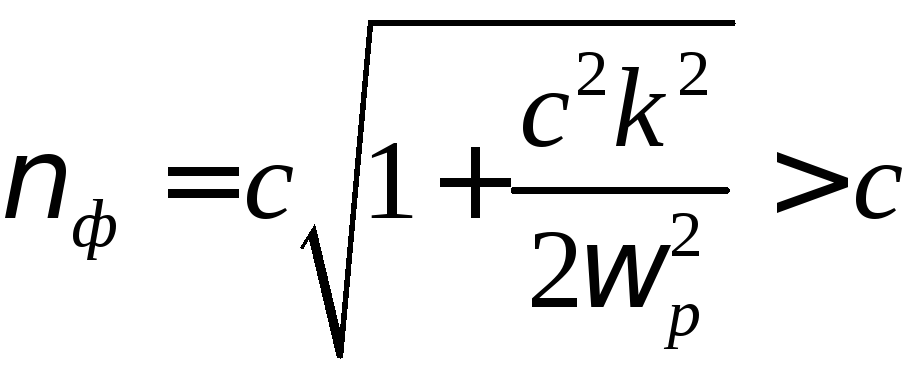
больше скорости света. Поэтому для таких волн несущественны резонансные эффекты. Просто потому, что их фазовая скорость заведомо превышает скорости частиц плазмы, всегда меньших скорости света. Подчеркнем, что групповая скорость поперечной волны, отвечающая за перенос волновой энергии,

,

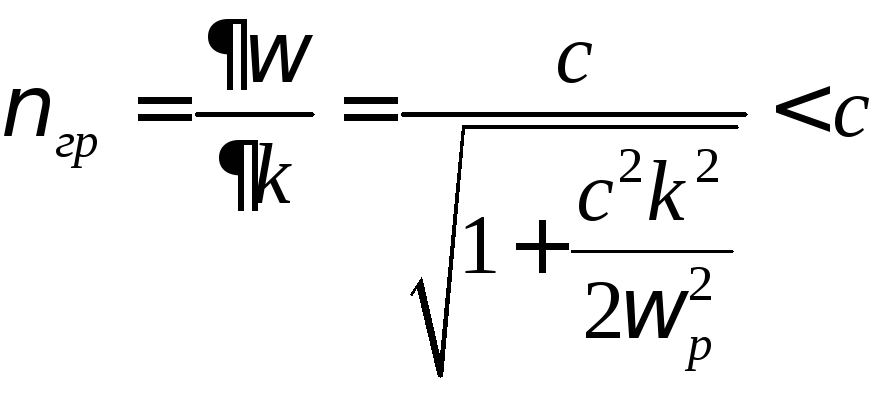оказывается, как это и должно быть, меньше скорости света в вакууме.

§ 30. Явление отсечки низкочастотной поперечной волны

Как мы видим из формулы (4.36), частота поперечной волны в плазме всегда больше плазменной частоты, поэтому поперечные волны, частота которых меньше плазменной частоты, не могут в ней распространяться. Это означает, что падающая из вакуума на границу плазмы поперечная волна с малой частотой должна отражаться. Имеет место, как говорят явление отсечки волны (в английской литературе – cut off). Критическая частота -частота отсечки

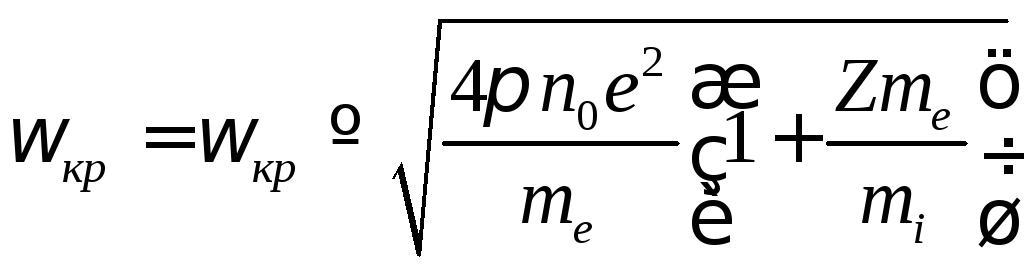
зависит от концентрации плазмы. Так что, измеряя критическую частоту, можно определить концентрацию плазмы. Это один из распространенных методов диагностики плазмы.

Электромагнитное поле низкочастотной волны частично все же проникает в плазму, но его амплитуда експоненциально уменьшается вглубь плазмы. Глубина проникновения в плазму поля поперечной волны с низкой частотой определяется толщиной вакуумного скин-слоя, которая обратно пропорциональна плазменной частоте:

.

Таким образом, глубина проникновения волны в плазму определяется инерцией ее частиц, главным образом электронов. В пренебрежении инерцией глубина проникновения поля была бы нулевой.

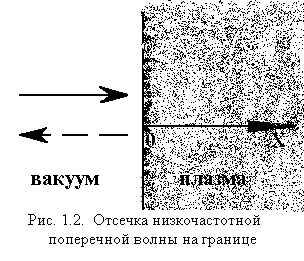
Проиллюстрируем сказанное простым примером. Пусть из вакуума на плоскую границу плазмы падает низкочастотная волна, слева направо, как это показано на рис. 1.2. Слева и справа от границы раздела законы дисперсии волны разные:

Эти соотношения можно записать в дифференциальном виде. Пусть частота волны фиксирована, заменив

получим уравнения

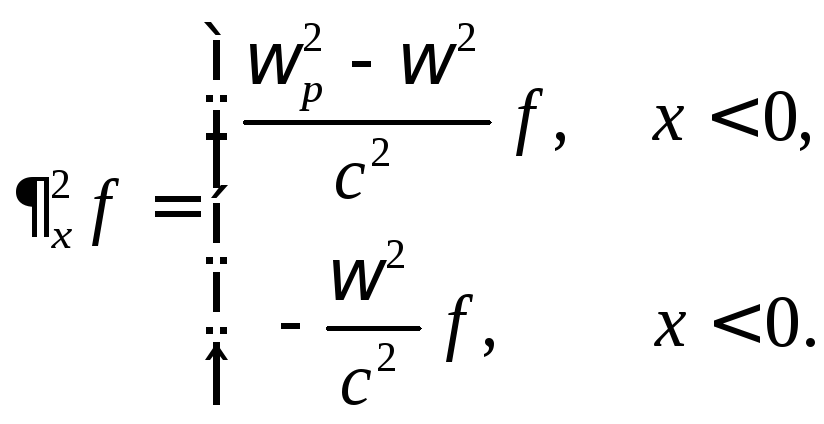
где функция f задает поле волны: например, это может быть компонента напряженности электрического поля. На границе раздела потребуем выполнения условий непрерывности:

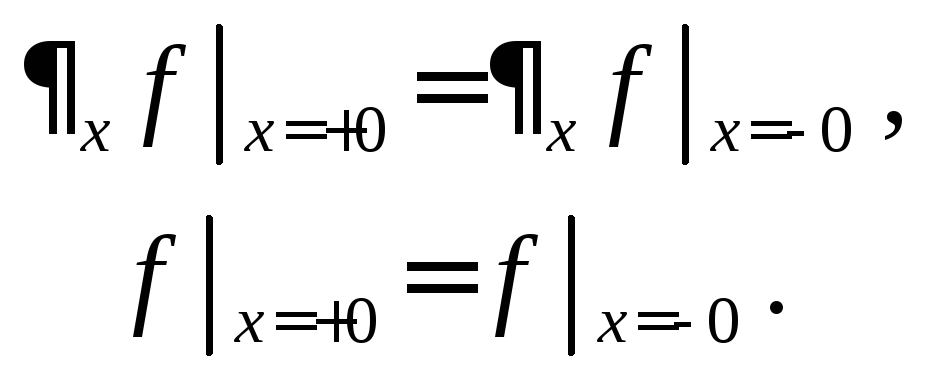
Нетрудно найти решение задачи (4.39), (4.40), удовлетворяющее этим условиям. Предлагаем читателю проверить, что таковым является решение, в котором в области вакуума поле складывается из поля падающей и отраженной волны, а в области плазмы волновое поле экспоненциально затухает:

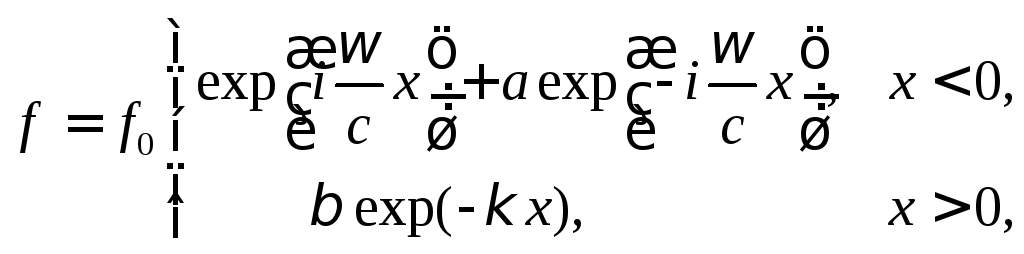
где

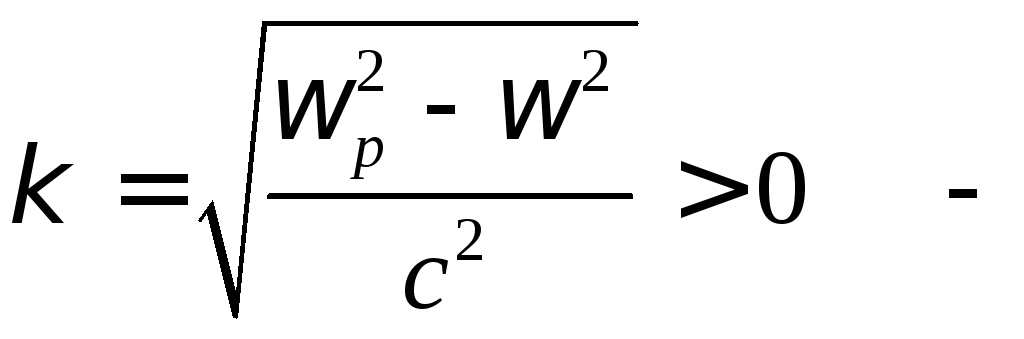
коэффициент пространственного затухания поля волны в плазме, - амплитуда падающей на границу раздела волны. Амплитудные коэффициенты для отраженной волны и для поля в плазме, как это вытекает из условий непрерывной сшивки (4.40), оказываются равными:

Обратим внимание, что числитель и знаменатель первой формулы являются комплексно-сопряженными. Поэтому получаем

,

и, следовательно, амплитуды падающей волны и отраженной совпадают. Это и означает наличие полного отражения падающей на плазму волны.

В пределе совсем низких частот, когда получаем приближенно

и длина затухания поля в плазме совпадает с длиной вакуумного скин-слоя.