§ 28. Метод малых колебаний. Диэлектрическая проницаемость незамагниченной плазмы.

Как следует из изложенного в предыдущем параграфе, все свойства волн, способных распространяться в данной среде, в том числе и в плазме, определяются ее диэлектрической проницаемостью. Поэтому наша ближайшая цель установить и исследовать диэлектрические свойства плазмы. Прежде чем перейти к рассмотрению конкретных плазменных волн напомним два результата, которые мы уже обсуждали ранее. Во-первых, диэлектрическая проницаемость холодной плазмы должна определяться соотношением:

,

где -частота колебаний, а -ленгмюровская (или плазменная) частота. Возникает вопрос, какую плазму можно назвать холодной? Для ответа на этот вопрос, очевидно, надо сопоставить характерные скорости движения частиц плазмы и фазовые скорости плазменных волн. Для равновесной плазмы характерная скорость движения частиц (в отсутствие волны!) это тепловая скорость (большая для электронов плазмы), поэтому, изучая условия распространения волн, плазму можно считать холодной при выполнении условия:

.

Поскольку это условие ограничивает частоту волн снизу, то оно отвечаетвысокочастотному пределу, а, следовательно, формула (4.19) определяет диэлектрическую проницаемость плазмы в высокочастотном пределе.

Во-вторых, напомним, что при обсуждении дебаевской длины экранирования было получено уравнение экранировки

где – радиус Дебая для плазмы. Экранировка здесь рассматривается как статический процесс, поэтому уравнение (4.21) отражает диэлектрические свойства плазмы в статическом пределе. Полагая в (4.21)

приходим к следующему результату:

,,

определяющему диэлектрическую проницаемость плазмы в статическом пределе, справедливом при выполнении условия, обратного по отношению к (4.19):

.

Подчеркнем, что в обоих предельных случаях структура оказывается следующей:

Первое слагаемое здесь единица вклад вакуума, а остальные два отвечают вкладу электронов и ионов соответственно. Вклад различных компонент оказывается аддитивным вследствие отсутствия взаимодействия между ними.

Чтобы составить более полную картину диэлектрических свойств незамагниченной плазмы, воспользуемся методом малых колебаний. Для упрощения, и здесь следует сразу оговориться, будем пренебрегать эффектами резонансных с волной частиц. Резонансные эффекты играют принципиальную роль во многих плазменных явлениях,например, в механизме бесстолкновительного затухания Ландау, но их учет требует усложнения описания плазмы, поэтому пока их не будем затрагивать.

Суть метода малых колебаний заключается в следующем. Привоздействии на первоначально невозмущенную плазму волны малой амплитуды логично ожидать появления малого отклика, поэтому можно воспользоваться разложением величины этого отклика по амплитуде волны,

пренебрегая нелинейными эффектами. Кроме того, без учета резонансных эффектов, движение частиц плазмы, индуцируемое волной, можно рассматривать с помощью гидродинамических уравнений, записав для каждого сорта частиц уравнения движения и уравнения сохранения вещества.

Рассмотрим простейший пример: идеальную холодную плазму без пучков. Это значит, что мы пренебрежем тепловой скоростью частиц по сравнению со скоростью, приобретаемой ими в самосогласованых полях. Этот простой пример является удобной отправной точкой для более сложных ситуаций. В невозмущенном равновесном состоянии полагаем, что плотность плазмы однородная , нет внешнего электрического поля и потоков частиц . Под воздействием поля волны частицы плазмы придут в движение, получив ускорение, определяемое уравнениями движения:

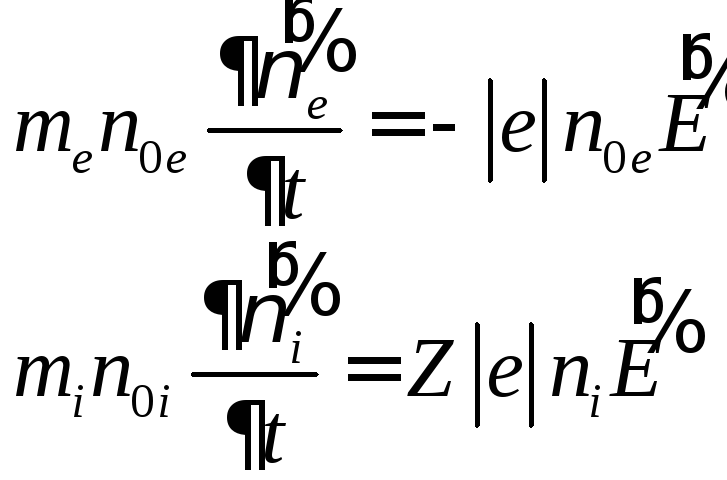
При записи (4.24) учли, что поле имеет малую амплитуду, поэтому все нелинейные слагаемые опущены. По этой же причине в правых частях фигурирует лишь действующая на частицы сила, обусловленная электрическим полем волны. Действуя по рецепту, предложенному в предыдущем

параграфе, считаем поле волны и скорости гармоническими,

.

Далее, с помощью (4.24) вычисляем скорости электронов и ионов, а затем и плотность тока, индуцируемого волной. Результат оказывается следующим:

.

Коэффициент пропорциональности между плотностью тока и напряжен ностью поля волны дает величину проводимости плазмы, которая в рассматриваемом пределе оказывается равной

Вклад в проводимость дают обе компоненты плазмы, но, естественно, не в равной мере. Обычно электронный вклад является доминирующим. Воспользовавшись теперь определением (4.10), можно вычислить диэлектрическую проницаемость, которая, как нетрудно проверить, совпадет с приведенной выше величиной (4.19).

Усложним модель плазмы, вводя в рассмотрение возможность передачи импульса в столкновениях между ионами и электронами. Учет этого эффекта приводит к появлению в уравнениях движения дополнительных слагаемых, происхождение которых взаимное трение компонент плазмы:

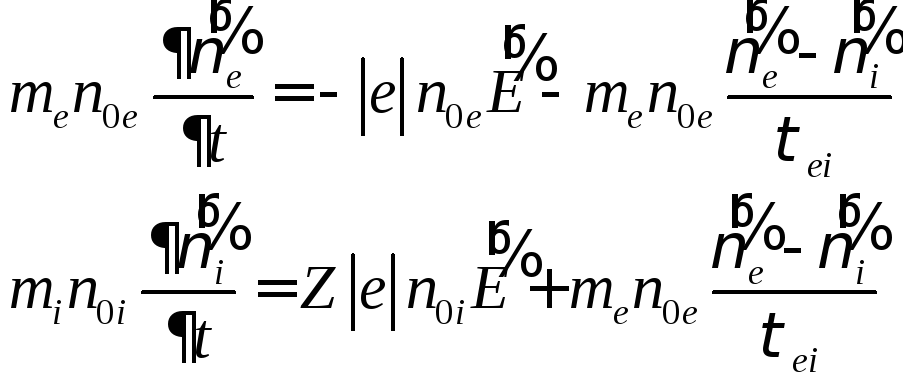
Вычисление скоростей компонент плазмы теперь несколько усложняется, но его можно упростить, если учесть следующее обстоятельство. Заметим, что любой выделенный единичный объем плазмы в нашей модели является нейтральным по заряду. Поэтому действующие на него электрические силы компенсируют друг друга. Кроме того, передача импульса между ионами и электронами не меняет в целом импульса выделенного объема плазмы! Поэтому, если импульс этого единичного объема первоначально был нулевым, то он остается таковым и в дальнейшем:

Это соотношение позволяет выразить одну скорость через другую, например ионную скорость через электронную скорость:

Уравнения (4.26) в результате сводятся к одному, например, уравнение движения электронов будет следующим:

и теперь уже несложно вычислить скорости и с их помощью плотность электрического тока. Для гармонической волны она оказывается равной:

,

и вновь пропорциональной полю волны. Здесь -частота электронионных столкновений, -проводимость плазмы. Для диэлектрической проницаемости:

.

Как мы видим, она становится величиной комплексной. Это является следствием того, что столкновения приводят к затуханию колебаний, то есть к диссипации энергии. Заметим, что в (4.28) теперь уже нельзя выделить отдельно вклад ионов и электроновАддитивность вкладов нарушается из-за взаимодействия компонент плазмы. Подчеркнем еще одно важное обстоятельство. Использованные в (4.26) выражения для плотности сил взаимного трения между электронами и ионами

,

или между ионами и электронами

,

отличаются по знаку - так и должно быть для сохранения импульса в целом в ионэлектронной системе, но, на первый взгляд, несимметричны при «буквенной» перестановке масс, зарядов и концентраций частиц. В действительности, необходимая симметрия имеет место. Достаточно вспомнить, что, как это было показано в § 9, эти параметры должны входить в выражение для времени между столкновениями ионов и электронов следующим образом:

,.

Теперь, после подстановки в выражения для плотностей сил трения, требуемая симметрия становится очевидной.

В уравнениях (4.24), (4.26) мы пренебрегли эффектами, связанными с конечностью температуры плазмы, что справедливо в высокочастотной области, когда выполнено условие (4.20). Чтобы продвинуться вобласть меньших частот, когда фазовая скорость волны оказывается одного порядка с тепловыми скоростями частиц, необходимо усложнить модель плазмы, включая эффекты конечного давления, что мы и собираемся теперь сделать. Вместе с тем для упрощения будем пренебрегать столкновениями ионов и электронов. Это возможно, если температура достаточно велика. Напомним, что частота ион-электронных столкновений быстро убывает с ростом температуры:

Если температура плазмы конечная, то в правые части уравнений движения (4.24) необходимо добавить слагаемые с градиентом давления.

Пусть температура компонент плазмы постоянная, тогда градиент давления определяется градиентом возмущения плотности:

,

следовательно, уравнения движения необходимо дополнить уравнениями, определяющими возмущение плотности плазмы. Если число частиц плазмы сохраняется, то необходимые нам дополнительные соотношения дают уравнения непрерывности. Для малых возмущений на фоне однородной плазмы это уравнения вида:

Кроме модели плазмы с постоянной температурой, часто используется модель политропы, в которой давление и температура плазмы предполагаются степенными функциями плотности:

,

где соответствующий показатель политропы. Для этогослучая градиент давления для малых возмущений будет равен

.

Объединяя вместе все вышесказанное, приходим к следующей модели для «теплой плазмы»:

Здесь индекс обозначает «сорт» частиц плазмы -ион или электрон. Так, заряд электрона, а заряд иона. Вновь предполагая волны гармоническими, вычисляем возмущение плотности и скорости компонент плазмы:

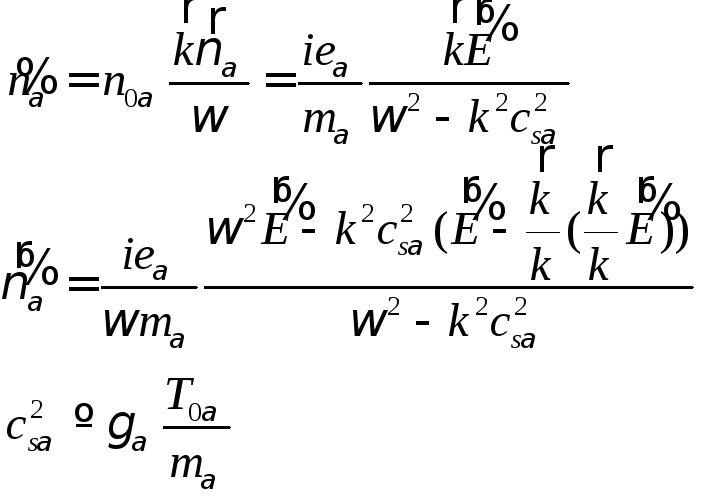
где, по аналогии с газом, для краткости введено обозначение для «скорости звука» соответствующей компоненты плазмы. Умножив найденные скорости компонент плазмы на заряд и невозмущенную плотность, просуммировав затем результат по сортам частиц, вычисляем плотность электрического тока:

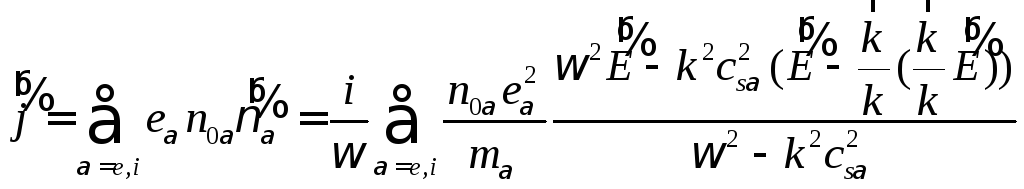
Воспользовавшись далее определениями (4.9), (4.10), получаем тензор проводимости:

а затем и тензор диэлектрической проницаемости:

В формулах (4.30), (4.31) индексы p, q нумеруют компоненты тензоров. Поскольку обсуждаемая нами сейчас модель плазмы в отсутствие волны является изотропной -нет никакого выделенного направления, то структура тензора диэлектрической проницаемости совпадает с предсказываемой формулой (4.14). Из сопоставления с этой формулой получаем продольную

и поперечную

диэлектрическую проницаемость. Они разные, поскольку учет теплового движения частиц плазмы приводит к появлению явной зависимости диэлектрической проницаемости от волнового числа. Сравнив (4.32), (4.33) с формулой (4.19) для холодной плазмы, мы видим, что изменение претерпевает только продольная диэлектрическая проницаемость, поперечная остается неизменной! Это связано с тем, что поперечная гармоническая волна малой амплитуды не изменяет плотности плазмы, следовательно, не появляется градиент давления, и конечность температуры несущественна.

В статическом пределе, т. е. в пределе , продольная проницаемость оказывается равной

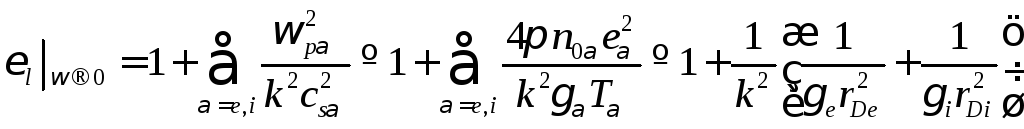
что совпадает с (4.22), если принять , т.е. считать компоненты плазмы изотермическими.

Подчеркнем, что, строго говоря, учет теплового движения частиц плазмытребует кинетического описания. Поэтому приведенные результаты дают качественно правильную, но упрощенную картину диэлектрических свойств плазмы. Можно добиться лучшего согласия с точными результатами, если входящие в приведенные формулы показатели ,рассматривать в качестве «подгоночных параметров», отбирая их в зависимости от конкретной решаемой задачи. Например, в случае, когда тепловые поправки можно считать малыми, но конечными, из формулы (4.32) приближенно получаем:

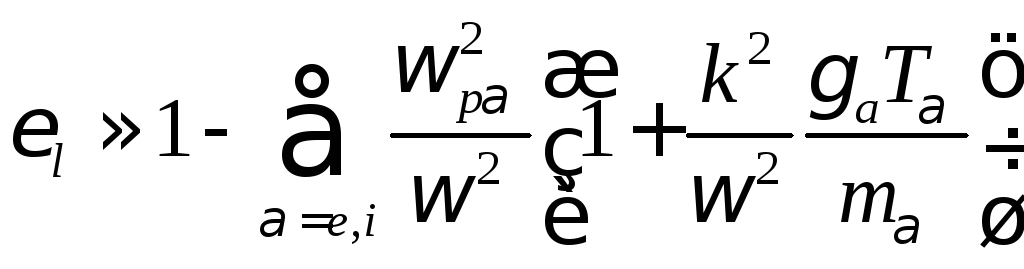
что совпадает с результатом кинетической теории [18] при выборе .