Глава 4
КОЛЕБАНИЯ И ВОЛНЫ В ПЛАЗМЕ. НЕУСТОЙЧИВОСТИ ПЛАЗМЫ.
Это очень интересный, но весьма сложный раздел физики плазмы. Плазма имеет много степеней свободы, ее свойства сильно меняются при наложении магнитного поля (возникает сильная анизотропия). По этой причине спектр возможных в ней колебаний и волн является весьма широким. Мы рассмотрим лишь некоторые, наиболее характерные примеры для изотропной (незамагниченной) плазмы и распространение простейших типов волн в замагниченной плазме. Более подробное изложение можно найти, например, в [18,19]. Обычно классификация типов волн начинается с разделения их на продольные и поперечные волны. Для механических волн продольность или поперечность волны связывают с характером движения в ней частиц − вдоль или поперек направления распространения волны. Например, звуковые волны, с помощью которых лектор доводит до своих слушателей информацию об обсуждаемом предмете, являются продольными – сгущения и разрежения газа, по сути дела и представляющие собой звуковую волну, происходят в направлении ее распространения. Для электромагнитной волны ее продольность или поперечность определяется взаимной ориентацией вектора распространения волны (волнового вектора) и вектора электрического поля волны. Если волновой вектор и вектор электрического поля волны коллинеарные, то такая волна является продольной. Если же плоскость колебаний вектора электрического поля перпендикулярна направлению распространения волны, то такая волна является поперечной. Примером строго поперечной волны может служить электромагнитная волна − свет в вакууме. Для поперечных волн в поперечной по отношению к направлению распространения волны плоскости, очевидно, можно ввести два независимых взаимно перпендикулярных направления. Соответственно, говорят о двух независимых поляризациях волны. В плазме, независимо от наличия или отсутствия внешнего магнитного поля, возможно распространение и продольных и поперечных волн, причем при наличии внешнего магнитного поля возможно распространение и продольных и поперечных волн как вдоль, так и поперек этого магнитного поля. В связи с этим важно не путать характер волны − продольная она или поперечная − и характер ее распространения: вдоль или поперек магнитного поля, в которое помещена плазма.
С возникновением и раскачкой колебаний и волн в плазме непосредственно связаны многие неустойчивости плазмы, которые будут обсуждаться в заключительном разделе этой главы.
§ 27. Дисперсионные уравнения для продольных и поперечных волн малой амплитуды.
Напомним кратко основные сведения из физики волновых процессов. Основным соотношением, определяющим условия распространения волны в данной среде, является закон дисперсии, устанавливающий связь частоты колебаний и волнового вектора:
.
Закон дисперсии позволяет определить фазовую скорость волны
и ее групповую скорость
.
Групповая скорость волны определяет перенос волновой энергии и поэтому никогда не может превышать скорость света в вакууме
.
Фазовая
скорость − скорость перемещения в волне
точек с постоянной фазой − не связана
с переносом волной энергии, а потому не
ограничена величиной скорости света.
В принципе, она может быть любой по
величине, в том числе и больше скорости
света, если это позволяет закон дисперсии.
Дисперсионные свойства данной среды,
если ограничиться областью волн малой
амплитуды, можно установить, рассматривая
отклик среды на малое воздействие. Для
волн конечной амплитуды ситуация
сложнее: такие волны изменяют свойства
среды, в которой распространяются.
Упрощенно это можно трактовать как
появление зависимости частоты колебаний
от амплитуды волны 
:
Такова ситуация для слабонелинейных волн, например, ленгмюровских солитонов [17]
Ограничимся
здесь рассмотрением волн малой амплитуды.
Универсальный подход, справедливый для
волн любой природы, заключается в
следующем. Электромагнитное поле волны
,
следует
определять из уравнений Максвелла:
Здесь 
,
−
наведенная в среде полем волны плотность
электрического заряда и плотность тока.
Эти величины не являются полностью
независимыми, а, как это следует из
(4.5), связаны соотношением
,
выражающем
собой закон сохранения заряда. В этом
нетрудно убедиться, применив операцию
дивергенции ко второму уравнению системы
(4.5).Поскольку коэффициенты уравнений
(4.5), (4.6) явно не содержат координат и
времени, можно искать решение в виде
гармонической волны 
.
Так как производные по времени и
координатам от гармонической волны
такого вида сводятся к алгебраическому
домножению на 
и 
соответственно,
,
,
то уравнения (4.5) при такой подстановке превращаются в алгебраические:
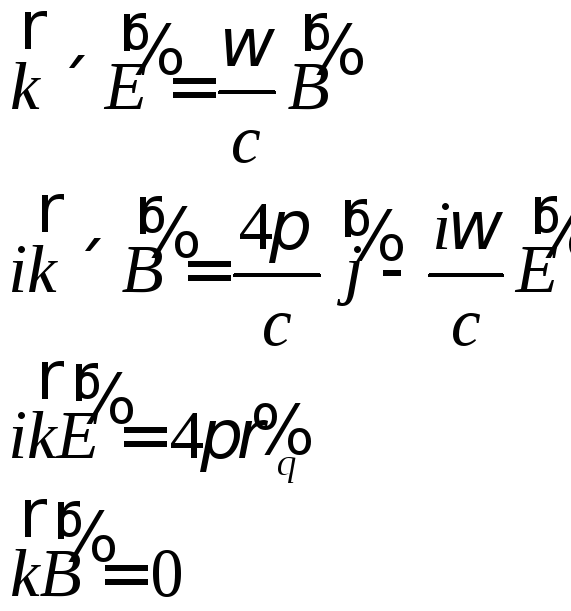
Первое из этих соотношений выражает магнитное поле волны через электрическое
,
и при таком определении, очевидно, последнее из соотношений (4.7) становится тождеством. Таким образом, соотношения (4.7) сводятся к следующим:
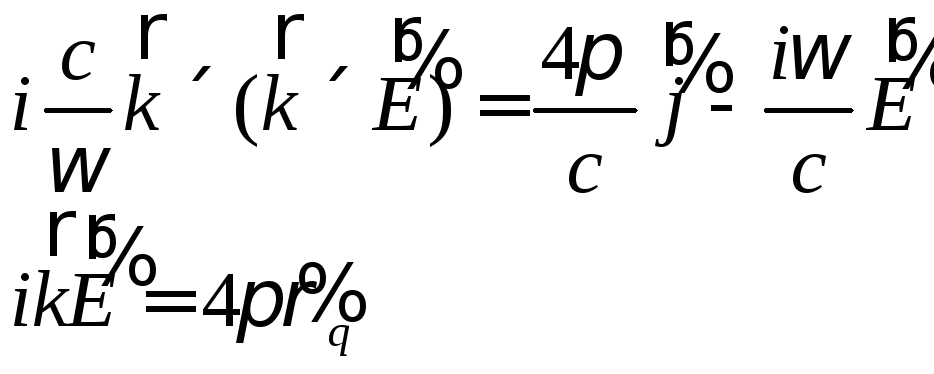
До сих пор мы не высказывали никаких предположений о связи наведенной волной в среде плотности тока (или заряда) и ее электромагнитного поля. Как это принято, для волн малой амплитуды эта связь предполагается линейной:
,
а набор
соответствующих коэффициентов
пропорциональности составляет тензор
проводимости 
, зависящий от свойств рассматриваемой
среды, а также, вообще говоря, от частоты
волны и волнового вектора. По определению
этот тензор связан с тензором
диэлектрической проницаемости 
среды
соотношением:
,
где первое слагаемое − единичная диагональная матрица. Поскольку, в силу (4.6), наведенная плотность заряда должна быть связана с наведенной плотностью тока соотношением
,
то второе из соотношений (4.8) фактически является следствием первого. По этой причине, с учетом определения тензора диэлектрической проницаемости, после простых преобразований приходим к однородной алгебраической задаче:
,
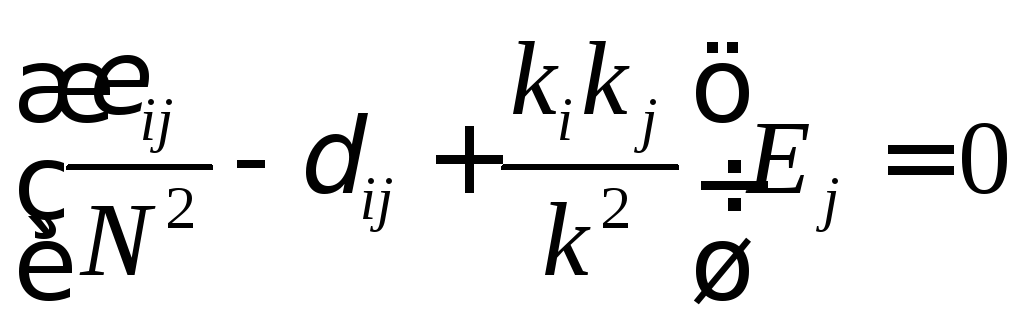где величина
представляет собой квадрат показателя преломления волны. Однородная задача (4.11), как известно, имеет ненулевое решение не всегда, а только при выполнении дополнительного условия. А именно, детерминант входящей в (4.11) матрицы должен быть равен нулю:
.
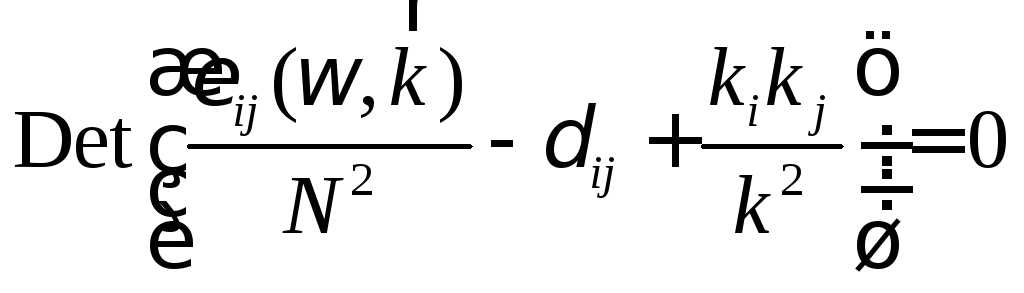Это условие и представляет собой дисперсионное уравнение, определяющее закон дисперсии (4.1) волн, способных существовать в данной среде. Если дисперсионное уравнение имеет несколько решений, то о них говорят как о ветвях или о модах собственных колебаний.
Если
среда, в которой рассматривается
распространение волны, изотропна, так
что единственным выделенным направлением
является направление распространения
самой волны, то среди всех компонент
тензора диэлектрической проницаемости
отличны от нуля лишь две компоненты −
продольная 
и поперечная 
по отношению к направлению распространения
волны (здесь индексы 
и 
– начальные буквы английских терминов
longitudinal
– продольный и transversal
- поперечный). Тогда этот тензор оказывается
следующим:
,
а дисперсионное уравнение, как легко проверить, приводится к виду:
.
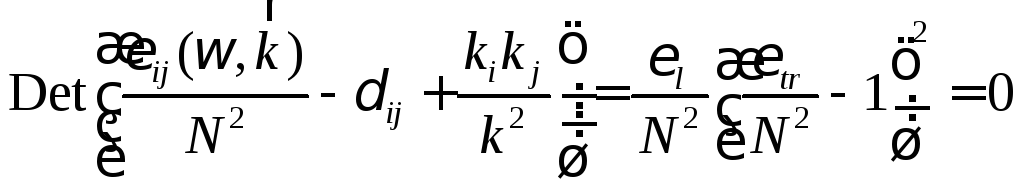Таким образом, как мы видим, существуют две возможности выполнить это условие:
,
.
Первая
из них отвечает продольным волнам, а
вторая − поперечным. Полезно отметить,
что если пространственная дисперсия
(т.е. зависимость компонент тензора
диэлектрической проницаемости от
волнового вектора) несущественна, то
продольная и поперечная компоненты
совпадают 
и можно
говорить лишь об одной величине 
– диэлектрической проницаемости среды.
Она и определяет дисперсионные уравнения
для продольных
,
и поперечных волн
.
Например, в вакууме, когда, очевидно, проводимость равна нулю, получаем из (4.10)
,
поэтому, согласно (4.17), продольные волны невозможны, а закон дисперсии поперечных волн, как это следует из (4.18) и (4.12), оказывается следующим
.
Напомним, что поперечные волны могут иметь два независимых направления поляризации. Подчеркнем в заключение, что если плазма анизотропна, например, помещена в магнитное поле, или в ней распространяется пучок частиц, так что существует явно выделенное направление, то представление (4.14) для тензора диэлектрической проницаемости не справедливо, но закон дисперсии для продольных (или, точнее, «почти» продольных, подробнее см. [20]) волн по-прежнему определяется уравнением (4.15), если под «продольной» диэлектрической проницаемостью понимать величину
.