Курсовые / курсач по КТиСФ, ЭКТ-2, 2-ой семестр, Фокин

Московский институт электронной техники.

Кафедра КФН.

Курсовая работа

по курсу:

Квантовая теория и

статистическая физика.

Москва 2004

Введение.

Одной из основных задач механики армированных материалов является определение макроскопических упругих постоянных и исследование их зависимости от соответствующих постоянных компонентов, их объемных концентраций, виде армирования и т. п. Первым приближением в этом вопросе является применение схем В. Фойхта и Э. Рейсса, согласно которым предполагается, что при воздействии однородной нагрузки на структурно неоднородное тело деформации или напряжения соответственно постоянны. Определяемые таким путем макроскопические упругие постоянные представляют математические ожидания соответственно упругих модулей и податливостей.

Результаты, полученные З. Хашиным и С. Штрикманом на основе вариационных принципов, представляют верхние и нижние границы макроскопических модулей. Они значительно улучшены по сравнению с границами Фойхта и Рейсса.

В работе Р. Хилла рассмотрен так называемый «самосогласованный метод» определения макроскопических постоянных многокомпонентных сред, в основу которого положена дополнительная гипотеза о средних деформациях компонентов.

Применение теории случайных функций в задачах об определении макроскопических упругих постоянных проводилось в работах. При этом результаты, полученные на основе уравнения равновесия и уравнения совместимости, оказались различными.

В настоящей работе показывается, что все перечисленные выше результаты могут быть получены на основе методов теории случайных функций, причем достаточно рассматривать лишь уравнения равновесия.

Зернистые среды.

Стохастически армированный материал можно рассматривать как твердое тело, механические характеристики которого являются случайными функциями координат. Будем предполагать, что компоненты материала изотропны и зависимости между напряжениями, деформациями и температурой описываются законом Дюамеля-Неймана:

(1.1)

Здесь постоянные Ламе и коэффициент температурного расширения являются случайными функциями координат (будем считать их статистически однородными).

Если тело находится под воздействием однородных нагрузок и постоянной температуры, то напряжения и деформации в теле также будут статистически однородными случайными функциями координат.

Дадим определение математическому ожиданию функции и флуктуаций физической велечины. Математическое ожидание (среднее значение) одномерного распределения случайной величины x есть сумма произведений каждого значения x_i этой величины на ее вероятность (или интеграл по всей области определения в непрерывном случае):

Флуктуация физической величины­ – дисперсия:

или среднеквадратичное отклонение:

,

где

-единичный оператор.

Представим случайные функции в виде суммы математических ожиданий и флуктуаций:

,

, , (1.2)

Тогда, подставляя (1.1) и (1.2) в уравнение равновесия

(1.3)

получим уравнение относительно флуктуаций перемещений:

(1.4)

Положим, что характерный размер неоднородностей является микроскопическим, т.е. пренебрежимо малым в сравнении с размерами тела. В этом случае тело можно рассматривать как бесконечную среду, а флуктуации должны обращаться в нуль на бесконечности. При этом случайные функции , , , , будут удовлетворять свойству эргодичности. (Случайный процесс эргодичен, если с вероятностью, равной единице, все его статистические характеристики можно предсказать по одной реализации из ансамбля процесса с помощью усреднения по времени; иными словами, средние значения по времени почти всех возможных реализаций процесса с вероятностью единица сходятся к одной и той же постоянной величине (среднему значению по ансамблю). Или, среднее по времени равно среднему по реализациям. Благодаря свойству эргодичности значительно упрощается математический анализ случайных процессов.) Будем также заранее предполагать, что случайные поля статистически изотропны.

Для определения макроскопических упругих постоянных тела достаточно найти зависимость между математическими ожиданиями напряжений и деформаций, которые вследствие эргодичности равны средним по объему напряжениями и деформациям.

Подставляя (1.2) в (1.1), получим выражения для средних напряжений:

(1.5)

Поэтому для определения макроскопических постоянных необходимо на основе уравнения (1.4) найти моменты и как функции средних деформаций и подставить их в выражение (1.5).

Для определения моментов и удобно уравнение (1.4) привести к интегральному уравнению относительно флуктуаций деформаций. При этом коэффициентами главной части уравнения (1.4) можно взять некоторые произвольные постоянные l и m. Тогда придем к интегральному уравнению

, (1.6)

где функция Грина имеет вид

, (1,7)

Умножим уравнение (1.6) на выражение и проведем статистическое осреднение. Затем, интегрируя правую часть в пренебрежении угловыми составляющими двухточечных моментов, содержащих деформации, получим бесконечную систему уравнений относительно одноточечных моментов :

, (1.8)

Здесь введены следующие обозначения:

(1,9)

Система (1.8) может быть решена с помощью теории бесконечных определителей. Однако для двухкомпонентной среды задача существенно упрощается. В этом случае, исходя из общих свойств совместной плотности случайных функций легко установить, что моменты и имеют следующую структуру:

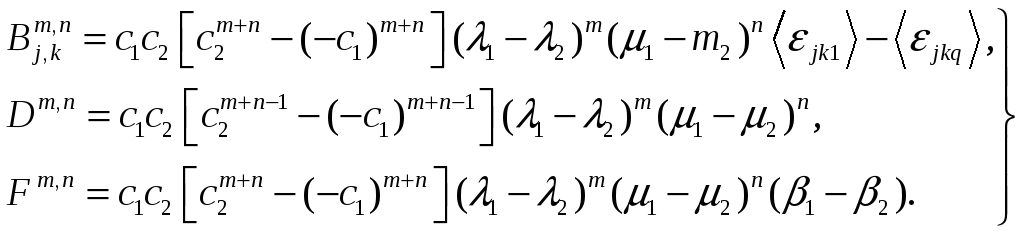(1.10)

Здесь и – соответственно объемные концентрации, термоупругие постоянные и средние деформации первого и второго компонентов.

Отсюда следует, что между моментами различных порядков существуют зависимости

. (1,11)

Соотношения (1.10) позволяют замкнуть бесконечную систему уравнений (1.8), на основе чего определим моменты и , входящие в выражение (1.5). Тогда зависимости между средними напряжениями, деформациями температурой можно представить в виде

, (1.12)

где макроскопические объемный модуль , модуль сдвига и коэффициент температурного расширения определяются формулами

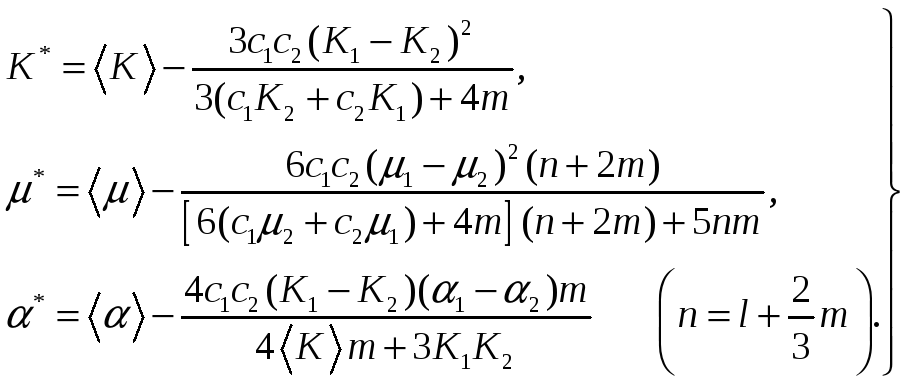(1.13)

Таким образом, несмотря на эквивалентность уравнений (1.4) и (1.6), выражения (1.13) оказались зависящими от постоянных и , что обусловлено допущенными пренебрежениями при решении уравнения (1.6).

Из выражений (1.13) могут быть получены следующие известные решения. При получим постоянные Рейсса, при – постоянные Фойхта.

Пусть ; тогда, полагая поочередно и , получим соответственно верхние и нижние границы Хашина – Штрикмана.

При получим решения, соответствующие общепринятому представлению, когда коэффициентами главной части уравнения равновесия (1.4) являются математические ожидания упругих моделей, т.е. будем иметь

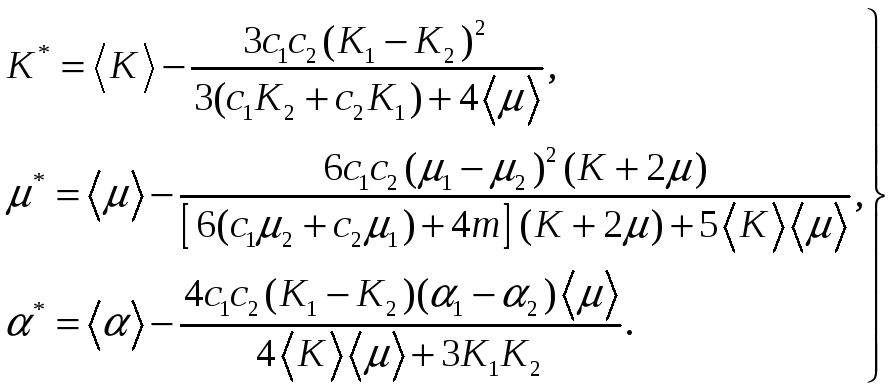(1.14)

Если в (1.13) положить , то получим формулы

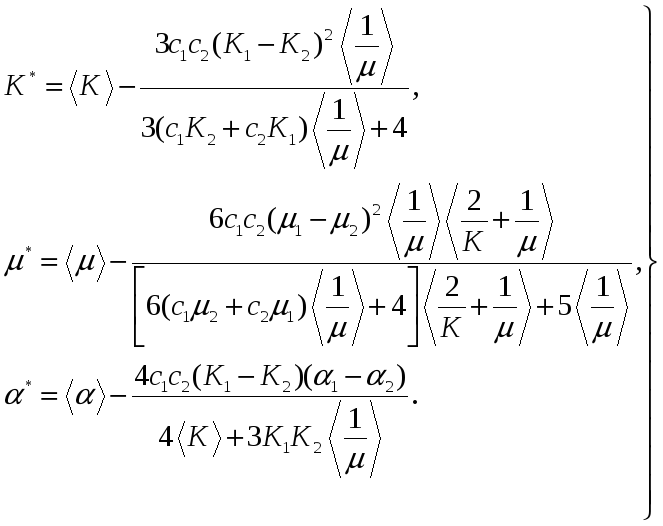(1.15)

которые совпадают с решением, полученным на основе уравнения совместности деформаций. При этом, как известно, оно соответствуют схеме композита, включения которого более жестки в сравнении с матрицей, в то время как формулы (1.14) соответствуют схеме композита с более жесткой матрицей.

Если в формулах (1.13) положить и , то после некоторых преобразований получим для определения макроскопических модулей , систему нелинейных уравнений

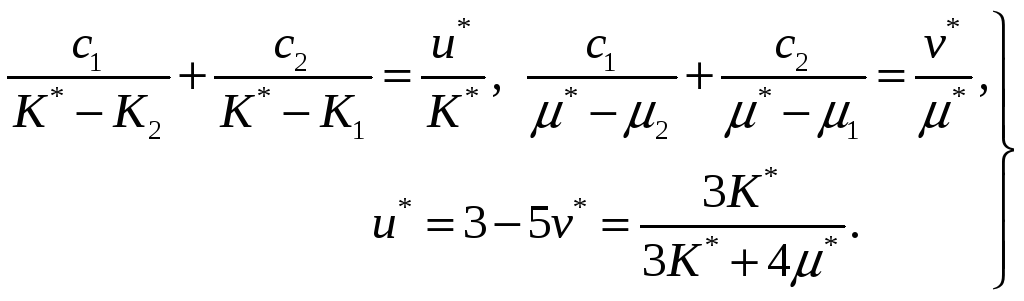(1.16)

которая совпадает с результатом применения «самогласованного метода».

При определении макроскопических постоянных на основе уравнения совместности деформаций можно также вместо математических ожиданий упругих податливостей взять коэффициентами главной части уравнения некоторые постоянные и , представив уравнение относительно флуктуаций напряжений в виде

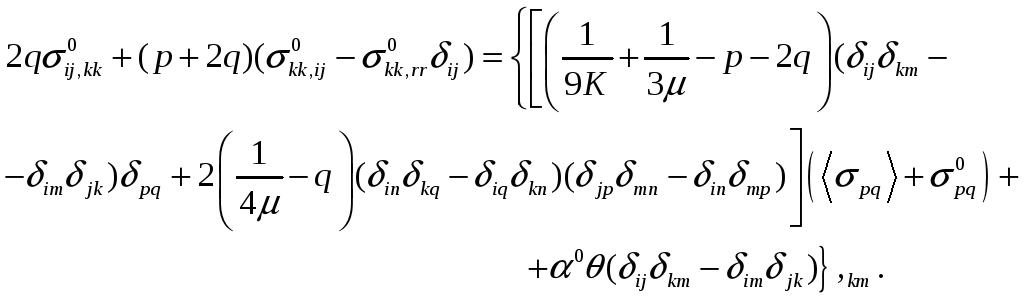(1.17)

Отсюда в пренебрежении угловыми составляющими двухточечных моментов, содержащих напряжения, получим бесконечную систему уравнений относительно одноточечных моментов. На основе ее решения для двухкомпонентной среды получим следующие выражения макроскопических постоянных:

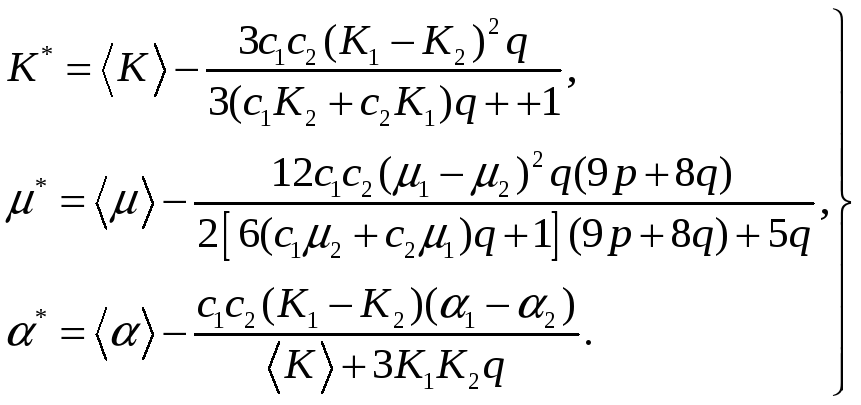(1.18)

Как видим, при и они совпадают с выражениями (1.13).

Однонаправленные волокнистые среды

Материалы, армированные однонаправленными хаотически расположенными волокнами, представляют среды, упругие модули которых являются случайными функциями координат плоскости. Вследствие хаотичности расположения волокон случайные поля и считаем статистически изотропными в поперечной плоскости.

Пусть волокна направлены вдоль оси . Тогда случайные функции зависят от координат и уравнение (1.4) распадается на два независимых уравнения:

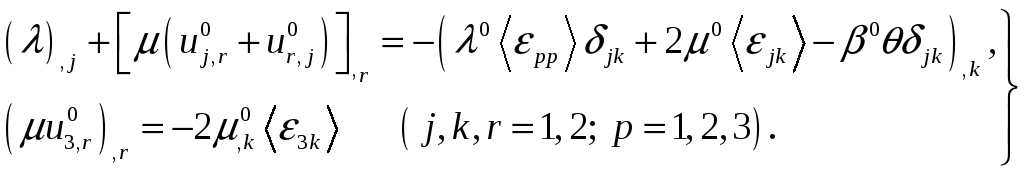(2.1)

Взяв коэффициентами главной части уравнения (2.1) некоторые постоянные l, m₁ и m₂, приведем их к интегральному уравнениям относительно флуктуаций деформаций:

(2.2)

где функции Грина имеют вид

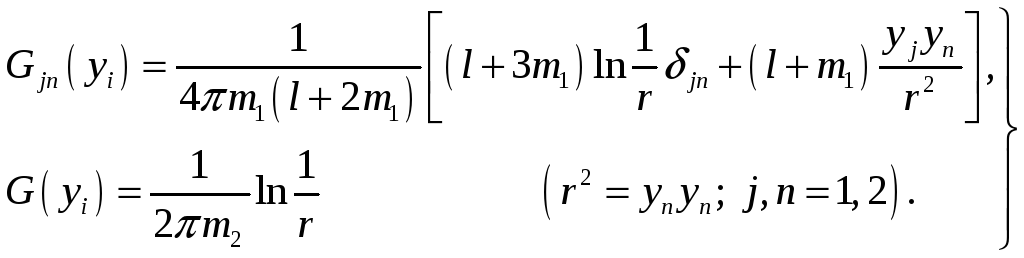(2.3)

Умножим уравнение (2.2) на выражение и проведем статистическое осреднение. Тогда в пренебрежении угловыми составляющими двухточечных моментов, содержащих деформаций, получим бесконечную систему уравнений относительно одноточечных моментов:

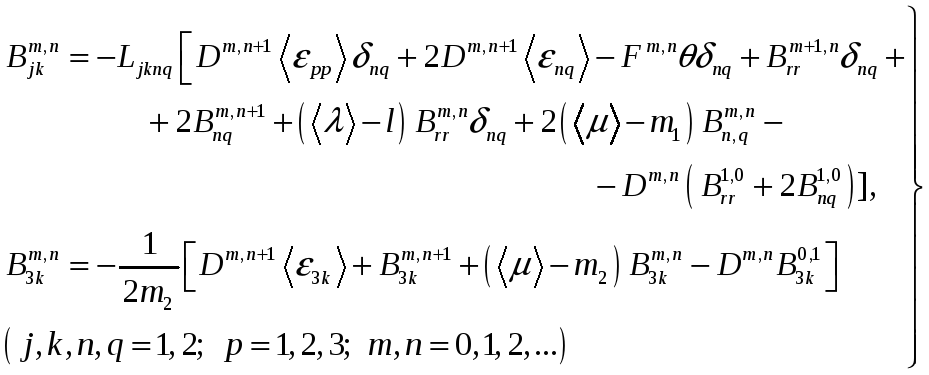(2.4)

где

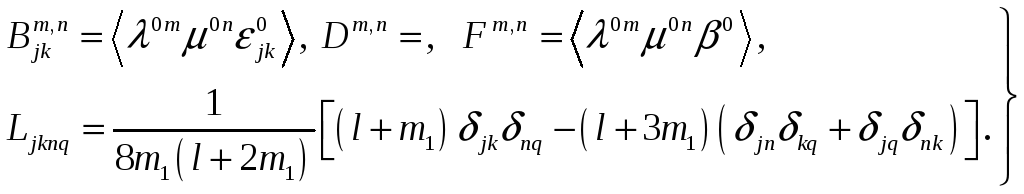(2.5)

Для двухкомпонентной среды, пользуясь соотношением (1.10) и (1.11), решение системы (2.4) находим в замкнутом виде. Подставляя моменты и в выражение (1.5), получим зависимость между средним напряжениями, деформациями и температурой:

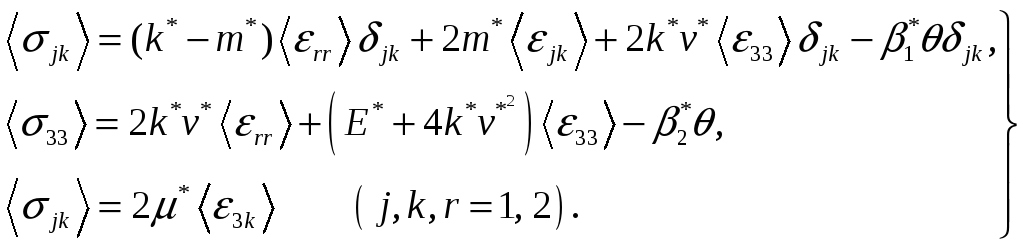(2.6)

Здесь макроскопические объемные модули плоской деформации , поперечный модуль сдвига , продольный модуль сдвига , продольный модуль Юнга и поперечный коэффициент Пуассона определяются формулами

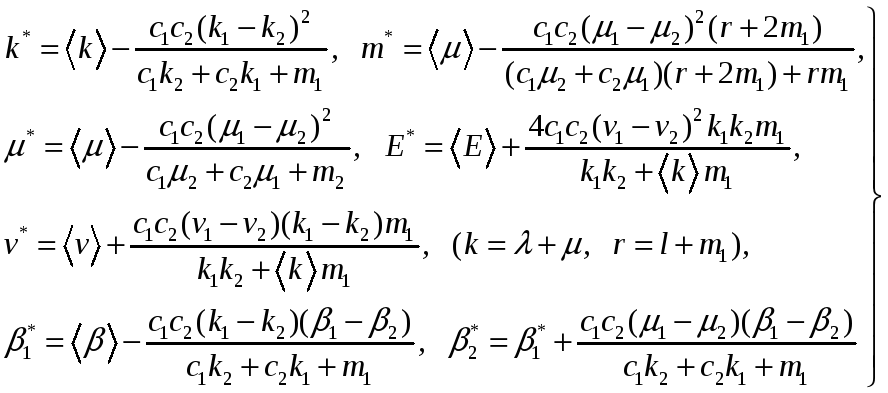(2.7)

При макроскопические постоянные (2.7) совпадают с постоянными Фойта для макроскопически изотропной среды. Если положить , то получим макроскопические постоянные, соответствующие известной схеме, которая предполагает, что напряжения и деформация волокон равны соответствующим напряжениям и деформации связующего.

Пусть ; тогда, полагая в (2.7) поочередно и , получим соответственно верхние и нижние границы Хашина-Штрикмана для однонаправленного волокнистого материала.

Полагая в (2.7) , получим макроскопические постоянные, соответствующие решению [14], когда коэффициентами главной части уравнений (2.1) являются математические ожидания упругих модулей, т.е. будет иметь

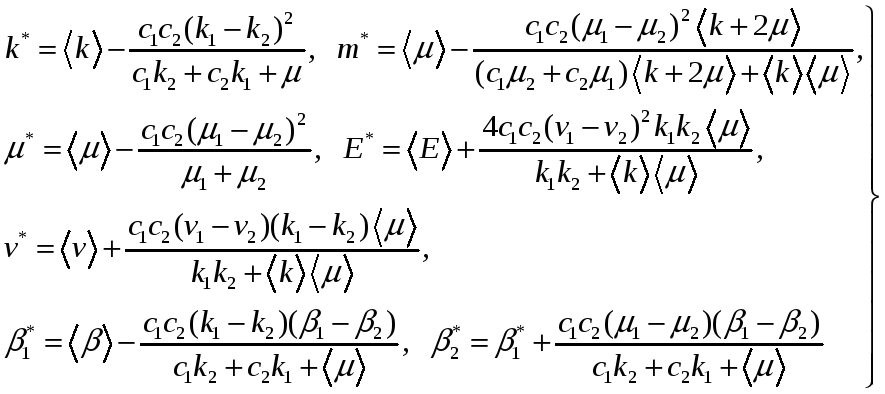(2.8)

Эти выражения соответствуют схеме композита с матрицей, боле жесткой в сравнении с волокнами.

Полагая в (2.7) , получим

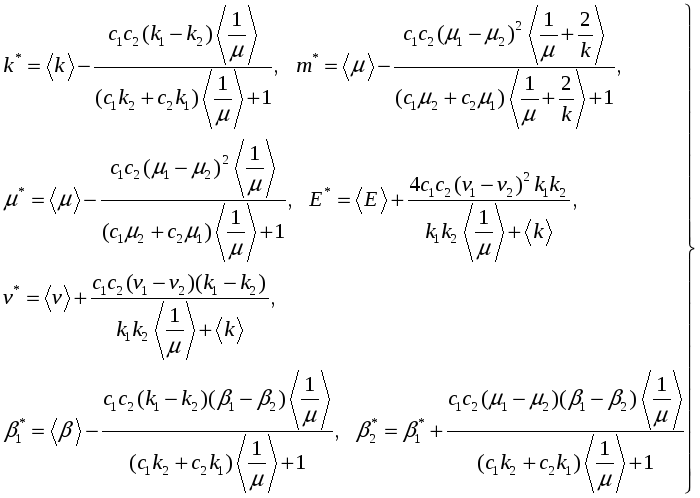(2.9)

Эти выражения совпадают с решениями на основе уравнения совместности деформаций, где коэффициентами главной части являются математические ожидания упругих податливостей. Они соответствуют схеме композита с более жесткими волокнами в сравнении с матрицей.

Если в (2.7) положить , то после преобразований получим для определения модулей сдвига кубическое и квадратичное уравнения:

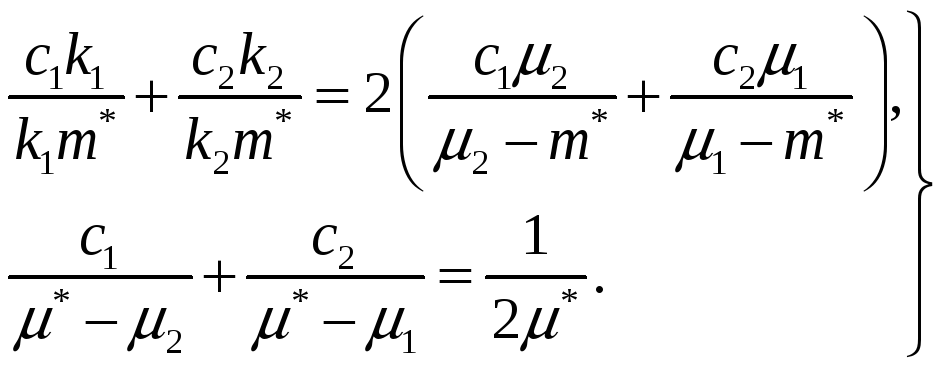(2.10)

Объемный модуль плоской деформации , модуль Юнга и коэффициент Пуассона определяются формулами:

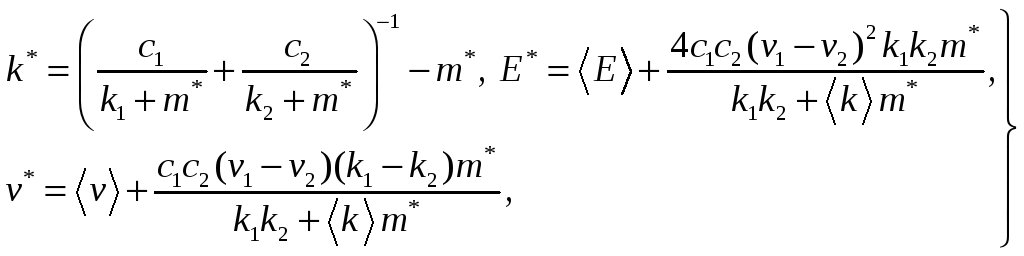(2.11)

Как видим, выражение (2.10) и (2.11) полностью совпадают с результатами «самосогласованного метода», для среды, армированной однонаправленным и волокнами.