Лекция 9 Неопределенность измерений

Основные положения

Неопределенность измерений – параметр, связанный с результатом измерений и характеризующий рассеяние значений, которые могут быть обоснованно приписаны измеряемой величине.

В соответствии со способом оценивания (рис. 9.1) все составляющие неопределенности можно сгруппировать в две категории:

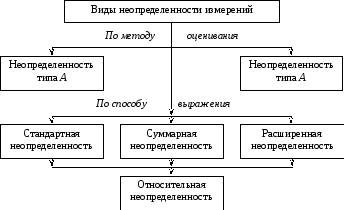
Рисунок 9.1 – Классификация неопределенностей измерений

А – составляющие, оцениваемые путем применения статистических методов (обработкой результатов многократных наблюдений). Составляющие типа А оцениваются как стандартные отклонения средних арифметических многократных наблюдений (неопределенности типа А – ). Эти составляющие характеризуются числами степеней свободы. Если между составляющими типаА наблюдается статистическая взаимосвязь (корреляция), то необходимо указывать коэффициенты корреляции ;

В – составляющие, оцениваемые другим способом (по характеристикам, взятым из предыдущих экспериментов, из паспорта на прибор, методик выполнения измерений, справочников и т.д.)..К источникам этих неопределенностей относятся: случайные погрешности однократных измерений; поправки, вводимые в результат измерения; неисключенные систематические погрешности, погрешности справочных данных и т.д. Составляющие типа В также оцениваются как предполагаемые стандартные отклонения, получаемые из известных границ, в которых могут находиться значения этих составляющих (неопределенности типа В – ). Между составляющими типаВ может существовать взаимосвязь, тогда следует указывать коэффициенты предполагаемой корреляции.

Суммарная стандартная неопределенность рассчитывается по правилу суммирования дисперсий.

Интервальной оценкой неопределенности является расширенная неопределенность , получаемая путем умножения стандартной суммарной неопределенностина коэффициент охвата. При указании расширенной неопределенности указывают уровень доверия – вероятность, которая обычно принимается равной 0,95.

По способу выражения неопределенность может быть стандартной, суммарной и расширенной. Все виды неопределенности могут выражаться в относительном виде.

Базовый алгоритм оценивания неопределенности измерений заключается в выполнении таких операций:

1) составление модельного уравнения;

2) оценивание значений входных величин, внесение поправок на известные систематические эффекты в результаты их измерений;

3) вычисление оценки результата измерений;

4) оценивание стандартных неопределенностей входных величин;

5) определение коэффициентов чувствительности;

6) вычисление вклада неопределенности каждой входной величины в неопределенность измеряемой величины;

7) определение попарной корреляции входных величин;

8) вычисление суммарной стандартной неопределенности измеряемой величины;

9) вычисление коэффициента охвата;

10) вычисление расширенной неопределенности измеряемой величины.

1. Составление модельного уравнения

Модельное уравнение выражает зависимость между выходной (измеряемой) величиной и входными величинами

.

В качестве входных величин в модельное уравнение, кроме непосредственно измеряемых величин, входят переменные, значения и неопределенности которых известны из внешних источников, а также поправки к результату измерения на известные систематические эффекты, основные и дополнительные абсолютные погрешности используемых средств измерительной техники.

Пример: При измерении напряжения постоянного тока с помощью вольтметра модельное уравнение имеет вид

,

где – индицируемое напряжение;– поправка на основную погрешность вольтметра;– поправка на температурную погрешность вольтметра;– поправка на погрешность отсчета вольтметра.