Neruh_Liniyna_algebra_Navch_posibn_2010_ukr / КНР-9_Задачи(207-)
.doc9 ІНДИВИДУАЛЬНІ ЗАВДАННЯ
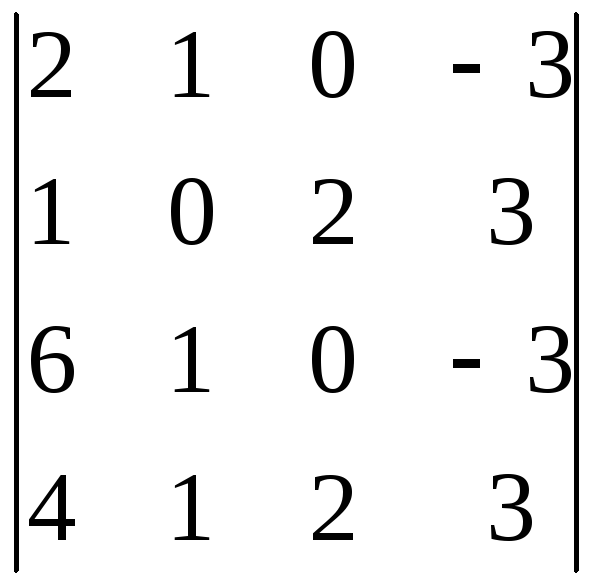
Задача 1. Обчислити визначник четвертого порядку.
|
1.1.
1.4.
1.7.
1.10.
1.13.
1.16.
1.19.
1.22.
1.25.
1.28.
|
1.2.
1.5.
1.8.
1.11.
1.14.
1.17.
1.20.
1.23.
1.26.
1.29.
|
1.3.
1.6.
1.9.
1.12.
1.15.
1.18.
1.21.
1.24.
1.27.
1.30.
|
Задача
2. Задані
матриці А
та
В.
Знайти
![]() .
.
2.1.
![]() . 2.2.
. 2.2.
![]() .
.
2.3.
![]() .
2.4.
.
2.4.
![]() .
.
2.5.
![]() . 2.6.
. 2.6.
![]() .
.
2.7.
![]() .
2.8.
.
2.8.
![]() .
.
2.9.
![]() . 2.10.
. 2.10.
![]() .
.
2.11.
![]() . 2.12.
. 2.12.
![]() .
.
2.13.
![]() .
2.14.
.
2.14.
![]() .
.
2.15.
![]() .
2.16.
.
2.16.
![]() .
.
2.17.
![]() . 2.18.
. 2.18.
![]() .
.
2.19.
![]() . 2.20.
. 2.20.
![]() .
.
2.21.
![]() . 2.22.
. 2.22.
![]() .
.
2.23.
![]() . 2.24.
. 2.24.
![]() .
.
2.25.
![]() . 2.26.
. 2.26.
![]() .
.
2.27.
![]() . 2.28.
. 2.28.
![]() .
.
2.29.
![]() . 2.30.
. 2.30.
![]() .
.
Задача 3. Розв'язати систему рівнянь двома способами: 1) матричним методом; 2) за формулами Крамера.
3.1.
 3.2.
3.2.

3.3.
 3.4.
3.4.

3.5.
 3.6.
3.6.

3.7.
 3.8.
3.8.

3.9.
 3.10.
3.10.

3.11.
 3.12.
3.12.

3.13.
 3.14.
3.14.

3.15.
 3.16.
3.16.
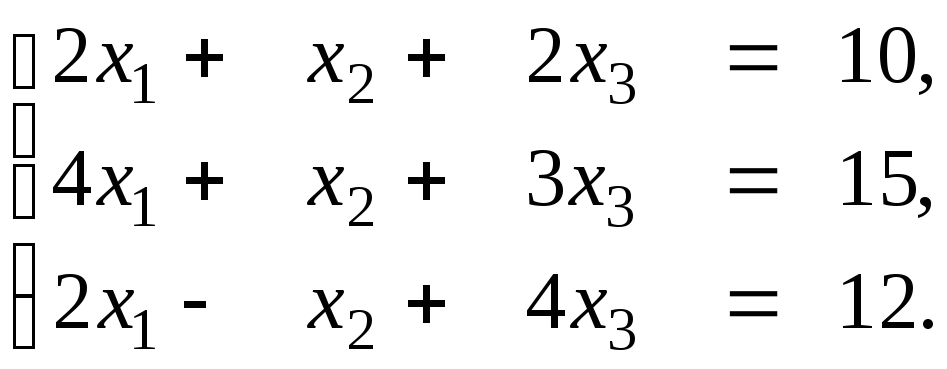
3.17.
 3.18.
3.18.

3.19.
 3.20.
3.20.

3.21.
 3.22.
3.22.

3.23.
 3.24.
3.24.
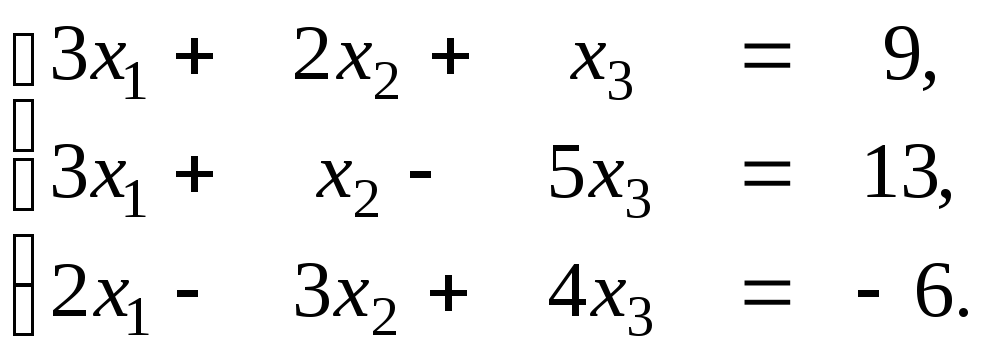
3.25.
 3.26.
3.26.

3.27.
 3.28.
3.28.

3.29.
 3.30.
3.30.

Задача 4. Дослідити сумісність системи і у випадку сумісності знайти загальний розв'язок системи. Знайти один частинний розв'язок та виконати перевірку правильності частинного розв'язку.
4.1.

4.2.

4.3.

4.4.

4.5.

4.6.

4.7.

4.8.

4.9.

4.10.
4.11.
4.12.
4.13.

4.14.

4.15.

4.16.

4.17.

4.18.

4.19.

4.20.

4.21.

4.22.

4.23.

4.24.

4.25.
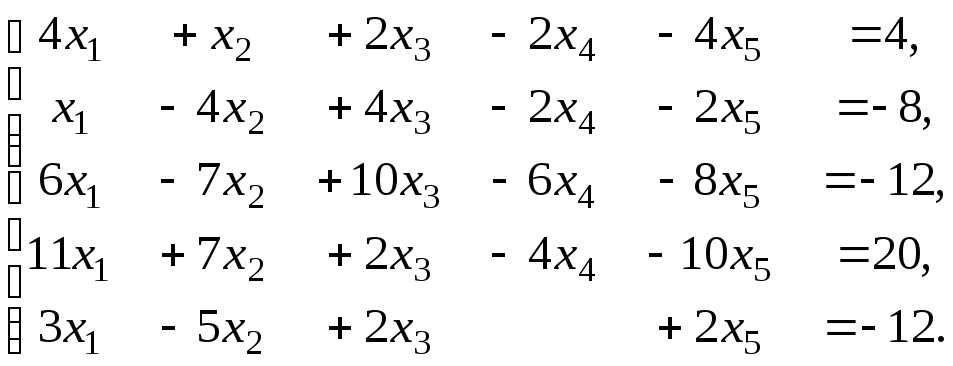
4.26.
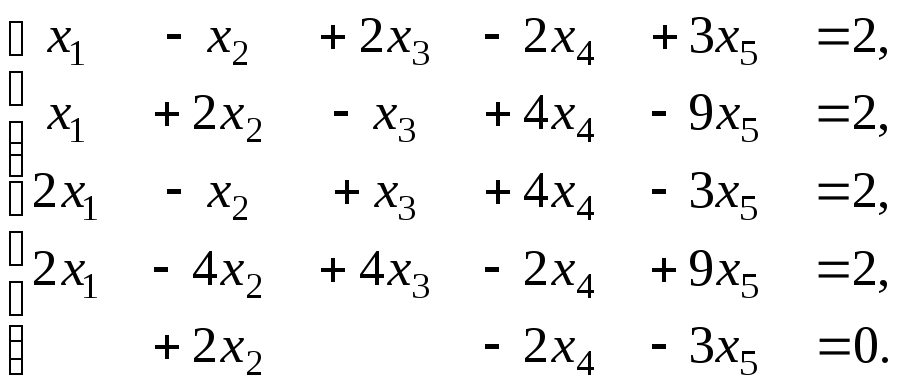
4.27.

4.28.

4.29.

4.30.

Задача 5. Дослідити наявність нетривіального розв'язку в однорідній системі рівнянь. Знайти її загальний розв'язок та фундаментальну систему розв'язків. Виконати перевірку правильності фундаментальної системи розв'язків.
5.1.

5.2.

5.3.

5.4.

5.5.

5.6.

5.7.

5.8.

5.9.
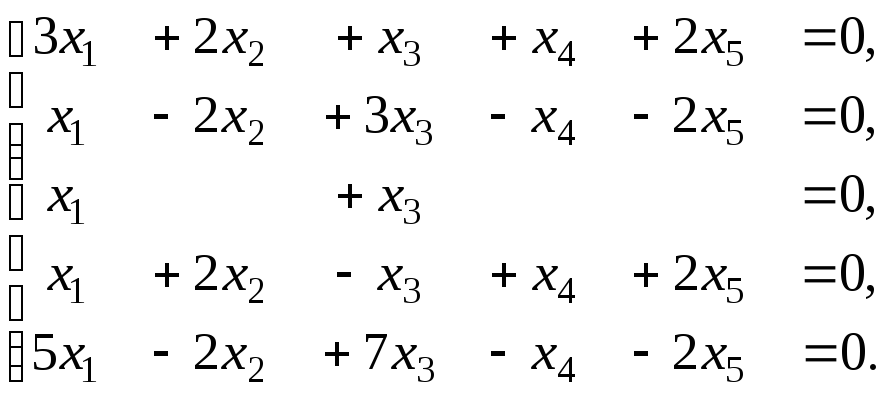
5.10.
5.11.

5.12.

5.13.
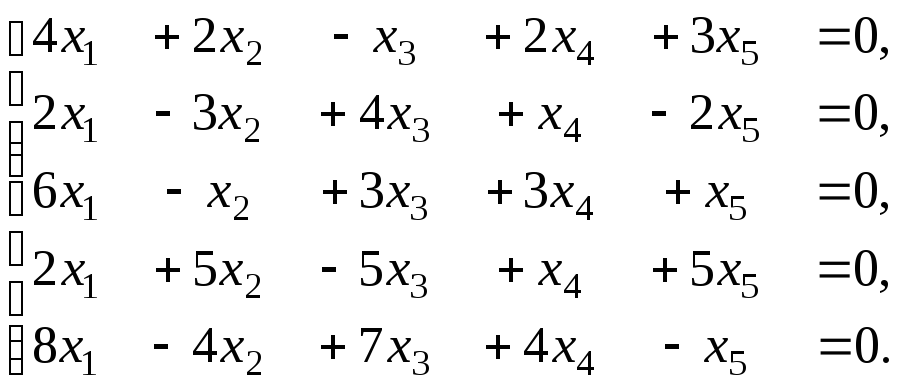
5.14.

5.15.

5.16.

5.17.

5.18.

5.19.
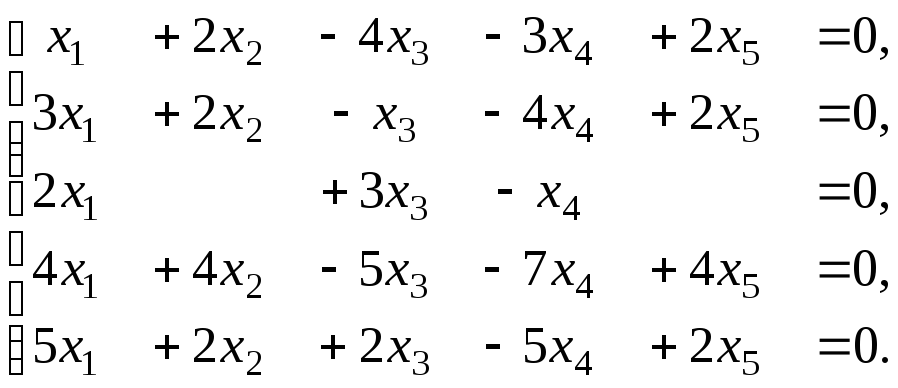
5.20.
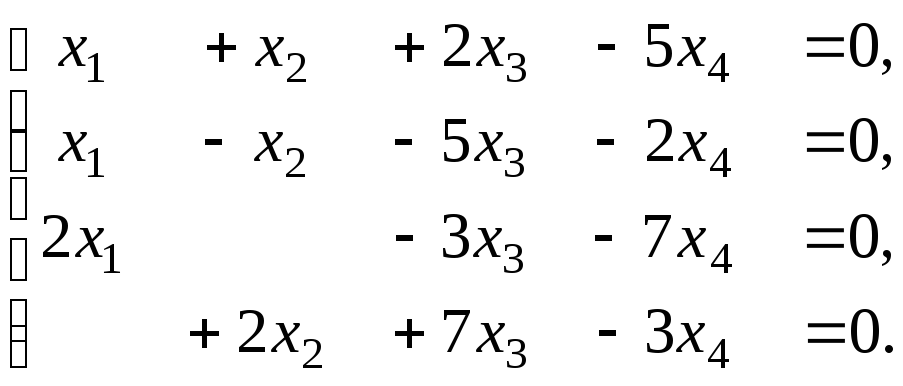
5.21.

5.22.

5.23.

5.24.

5.25.

5.26.

5.27.

5.28.
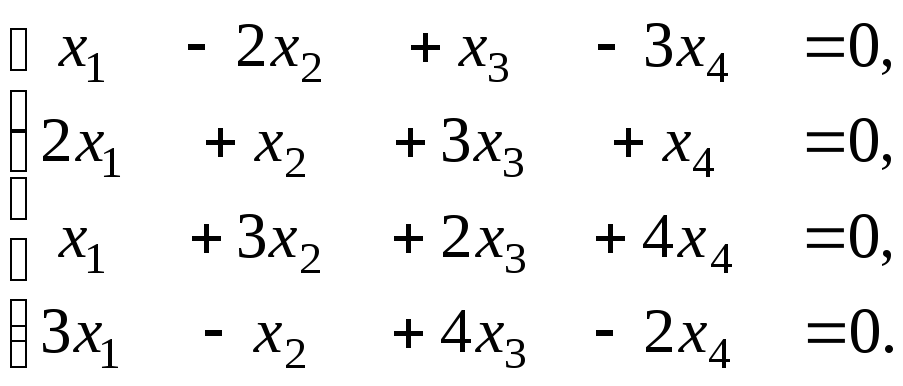
5.29.

5.30.
 .
.
Задача
6. Задані
чотири точки
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Визначити:
-
координати векторів
 ,
,
 ,
,
 ;
; -
довжину векторів
 та
та
 ,
де
,
де
 – орт вектора
– орт вектора
 ;
; -
скалярний добуток векторів
 ;
; -
косинус кута між векторами
 та
та
 ;
; -
 ;
; -
векторний добуток векторів
 та
та
 ;
; -
площу трикутника, побудованого на векторах
 та
та
 ;
; -
мішаний добуток векторів
 ,
,
 та
та
 ;
; -
об'єм трикутної піраміди, побудованої на векторах
 ,
,
 та
та
 ;
;
10) чи
колінеарні вектори
![]() та
та
![]() ;
;
11) чи
компланарні вектори
![]() ,
,
![]() та
та
![]() .
.
6.1.
![]()
6.2.
![]()
6.3.
![]()
6.4.
![]()
6.5.
![]()
6.6.
![]()
6.7.
![]()
6.8.
![]()
6.9.
![]()
6.10.
![]()
6.11.
![]()
6.12.
![]()
6.13.
![]()
6.14.
![]()
6.15.
![]()
6.16.
![]()
6.17.
![]()
6.18.
![]()
6.19.
![]()
6.20.
![]()
6.21.
![]()
6.22.
![]()
6.23.
![]()
6.24.
![]()
6.25.
![]()
6.26.
![]()
6.27.
![]()
6.28.
![]()
6.29.
![]()
6.30.
![]()
Задача
7. Для
заданих векторів
![]() і
і
![]() обчислити:
обчислити:
-
довжину вектора
 ;
; -
довжину вектора
 ;
; -
 ;
; -
косинус кута між векторами
 і
і
 ;
; -
площу паралелограма, побудованого на векторах
 і
і
 .
.
-
7.1.


 =3,
=3, =4.
=4.7.2.

 =
=
 =1,
=1, =4.
=4.7.3.
 =
= ,
, =
= ,
, =2,
=2, =2.
=2.7.4.
 =
= ,
, =
= ,
, =2,
=2, =3.
=3.7.5.
 =
= ,
, =
= ,
, =3,
=3, =3.
=3.7.6.
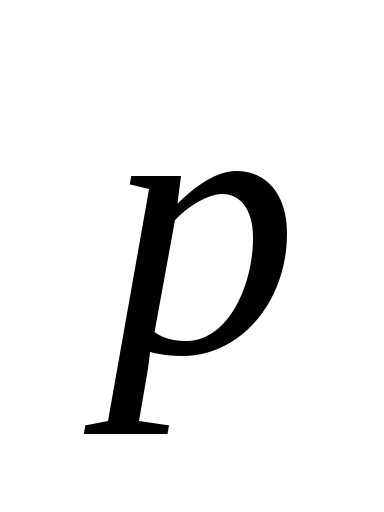 =
= ,
, =
= ,
, =2,
=2, =2.
=2.7.7.
 =
= ,
, =
= ,
, =2,
=2, =1.
=1.7.8.
 =
= ,
, =
= ,
, =2,
=2, =1.
=1.7.9.
 =
= ,
, =
= ,
, =1,
=1, =2.
=2.7.10.
 =
= ,
, =
= ,
, =1,
=1, =1.
=1.7.11.
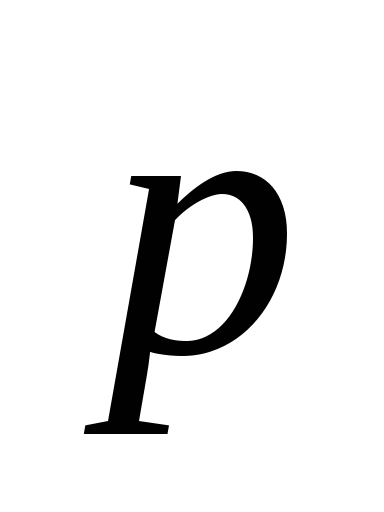 =
= ,
, =
= ,
, =3,
=3, =3.
=3.7.12.
 =
= ,
, =
=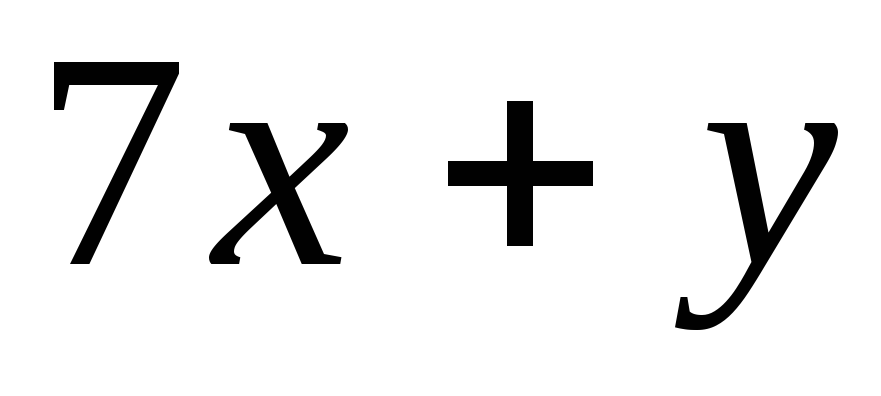 ,
, =2,
=2, =1.
=1.7.13.
 =
= ,
, =
=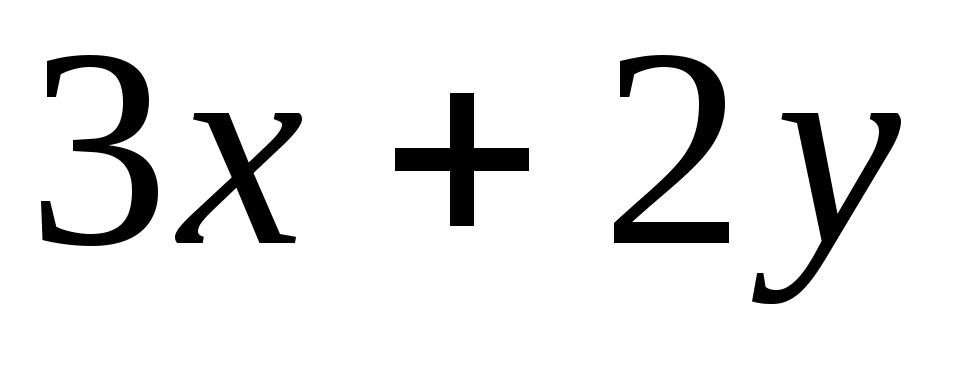 ,
, =1,
=1, =2.
=2.7.14.
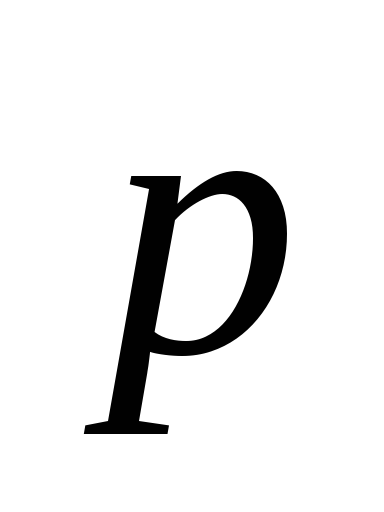 =
= ,
, =
= ,
, =1,
=1, =1.
=1.7.15.
 =
= ,
, =
= ,
,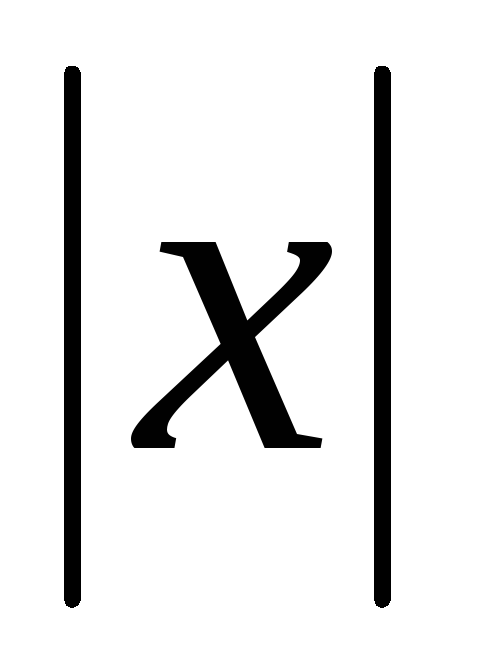 =1,
=1, =2.
=2.7.16.
 =
= ,
, =
= ,
, =2,
=2, =1.
=1.7.17.
 =
= ,
, =
= ,
, =4,
=4, =1.
=1.7.18.
 =
= ,
, =
= ,
, =1,
=1, =4.
=4.7.19.
 =
= ,
, =
=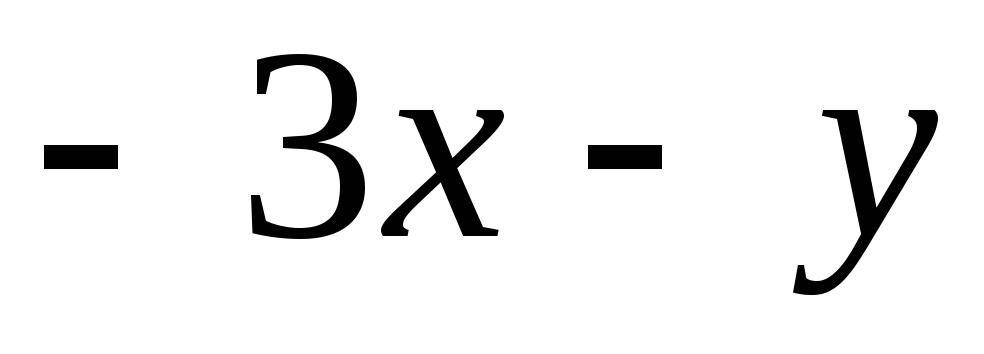 ,
,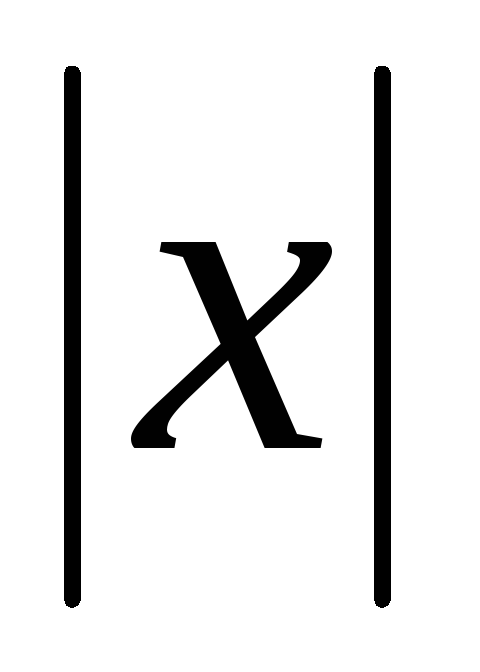 =4,
=4, =1.
=1.7.20.
 =
= ,
, =
=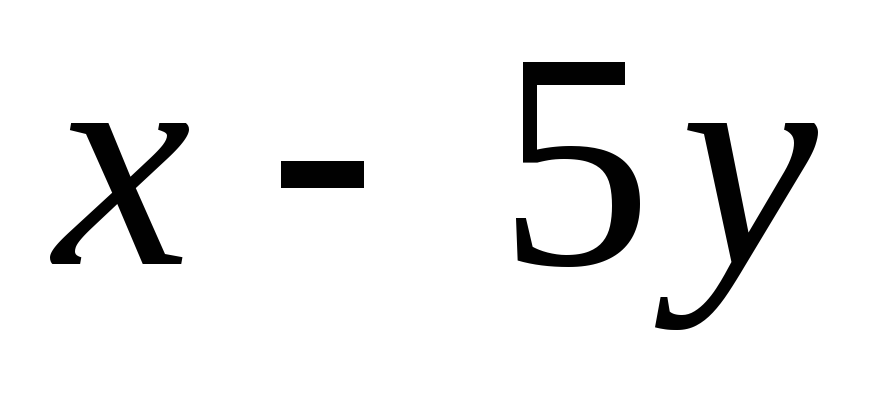 ,
, =1,
=1, =2.
=2.7.21.
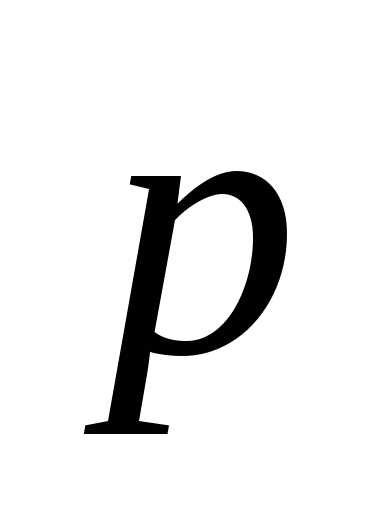 =
= ,
, =
= ,
, =2,
=2, =3.
=3.7.22.
 =
= ,
, =
= ,
, =2,
=2, =3.
=3.7.23.
 =
=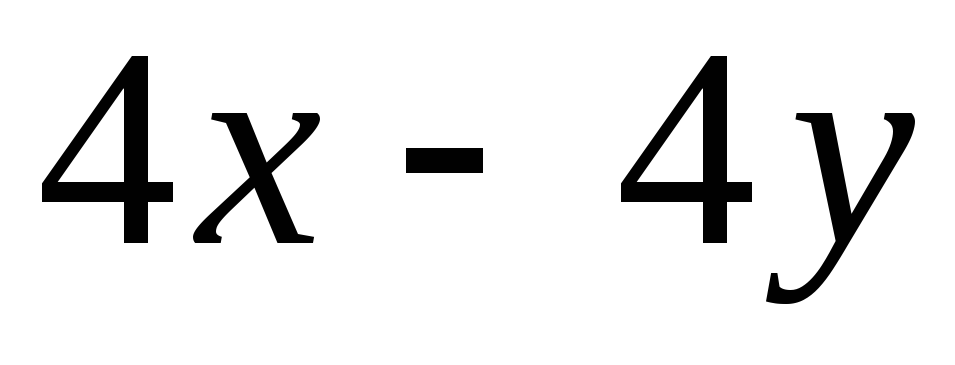 ,
, =
= ,
, =1,
=1, =1.
=1.7.24.
 =
= ,
, =
= ,
, =2,
=2, =2.
=2.7.25.
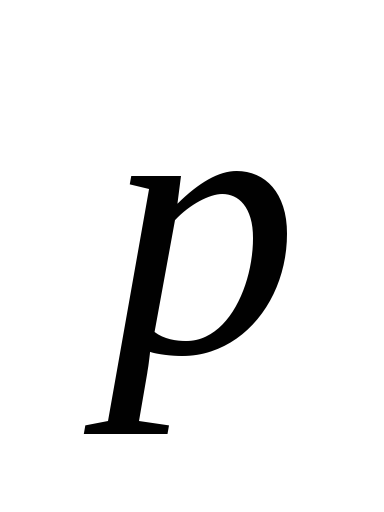 =
=
 =
= ,
, =1,
=1, =3.
=3.7.26.
 =
=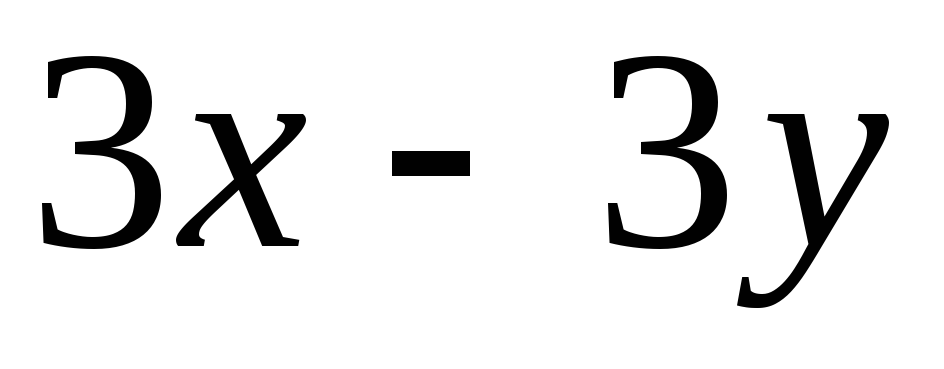 ,
, =
= ,
, =2,
=2, =1.
=1.7.27.
 =
= ,
, =
= ,
, =1,
=1, =1.
=1.7.28.
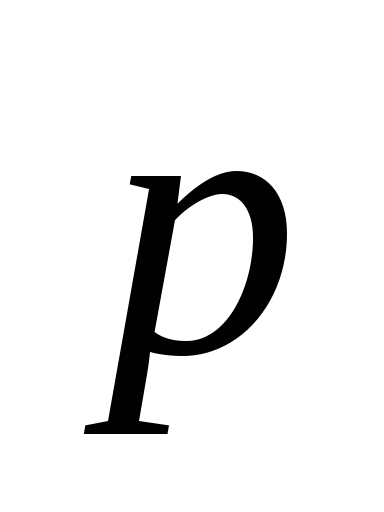 =
= ,
, =
= ,
,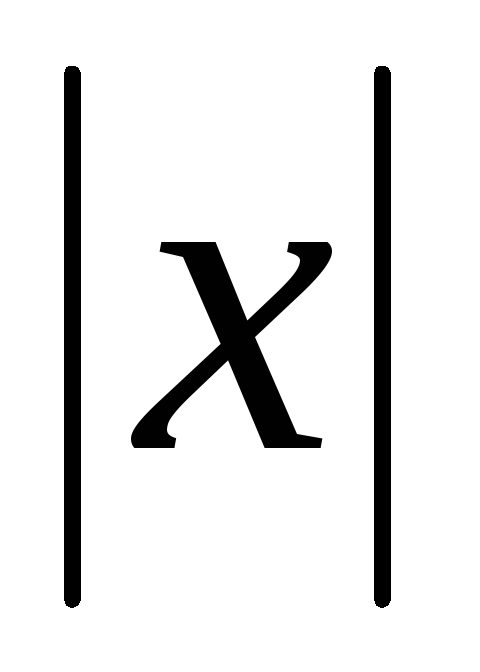 =1,
=1, =2.
=2.7.29.
 =
=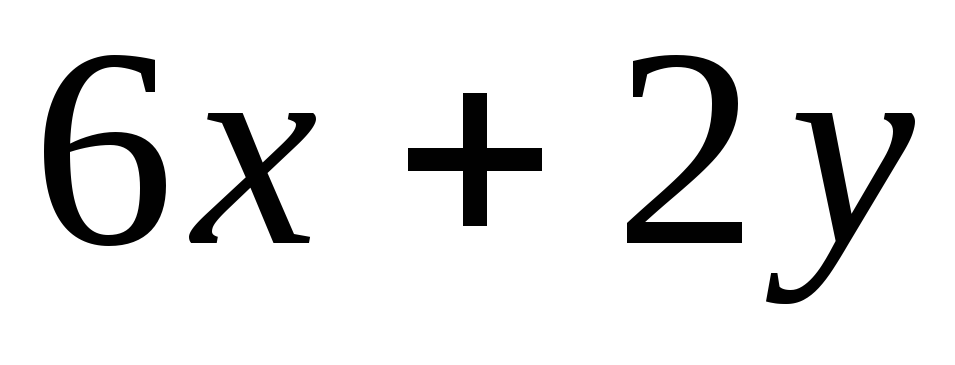 ,
, =
= ,
, =1,
=1, =1.
=1.7.30.
 =
= ,
, =
= ,
, =2,
=2, =2.
=2.