
answers (1)
.pdf
В1 |
Плавлением называется процесс перехода вещества |
|
A |
из жидкого состояния в газообразное, |
|
A |
из твердого состояния в газообразное, |
|
A+ |
из твердого состояния в жидкое, |
|
A |
из газообразного в жидкое |
|
В1 |
Конденсацией называется процесс перехода вещества |
|
A |
из жидкого состояния в газообразное, |
|
A |
из твердого состояния в газообразное, |
|
A |
из твердого состояния в жидкое, |
|
A+ |
из газообразного в жидкое |
|
В1 |
Диффузией называется |
|
A+ |
явление проникновения двух или нескольких соприкасающихся веществ одного в |
|
другое |
||
|
Aпроцесс перемещения молекул из тех частей вещества, где их концентрация больше, в те части, где их концентрация меньше,
Aпроцесс передачи тепла из одних частей вещества в другие, происходящий вследствие перемещения одних частей вещества относительно других,
Aпроцесс передачи тепла из одних частей вещества в другие, происходящий без перемещения одних частей вещества относительно других,
В1 |
Диффузионным потоком называется |
Aявление проникновения двух или нескольких соприкасающихся веществ одного в другое
A+ |
процесс перемещения молекул из тех частей вещества, где их концентрация |
|
больше, в те части, где их концентрация меньше, |
||
|
Aпроцесс передачи тепла из одних частей вещества в другие, происходящий вследствие перемещения одних частей вещества относительно других,
Aпроцесс передачи тепла из одних частей вещества в другие, происходящий без перемещения одних частей вещества относительно других,
В1 |
Конвекцией называется |
Aявление проникновения двух или нескольких соприкасающихся веществ одного в другое
Aпроцесс перемещения молекул из тех частей вещества, где их концентрация больше, в те части, где их концентрация меньше,
A+ |
процесс передачи тепла из одних частей вещества в другие, происходящий |
|
вследствие перемещения одних частей вещества относительно других, |
||
|
Aпроцесс передачи тепла из одних частей вещества в другие, происходящий без перемещения одних частей вещества относительно других,
В1 |
Теплопроводностью называется |
Aявление проникновения двух или нескольких соприкасающихся веществ одного в другое
Aпроцесс перемещения молекул из тех частей вещества, где их концентрация больше, в те части, где их концентрация меньше,
Aпроцесс передачи тепла из одних частей вещества в другие, происходящий вследствие перемещения одних частей вещества относительно других,
A+ |
процесс передачи тепла из одних частей вещества в другие, происходящий без |
||
перемещения одних частей вещества относительно других, |
|||
|
|||
В1 |
Число Авогадро равно |
||
A+ |
6,02 ×1023 |
моль−1 , |
|
A |
2,69×1025 |
м−3 , |
|
A |
8,31 Дж /(К × моль) , |
||
21
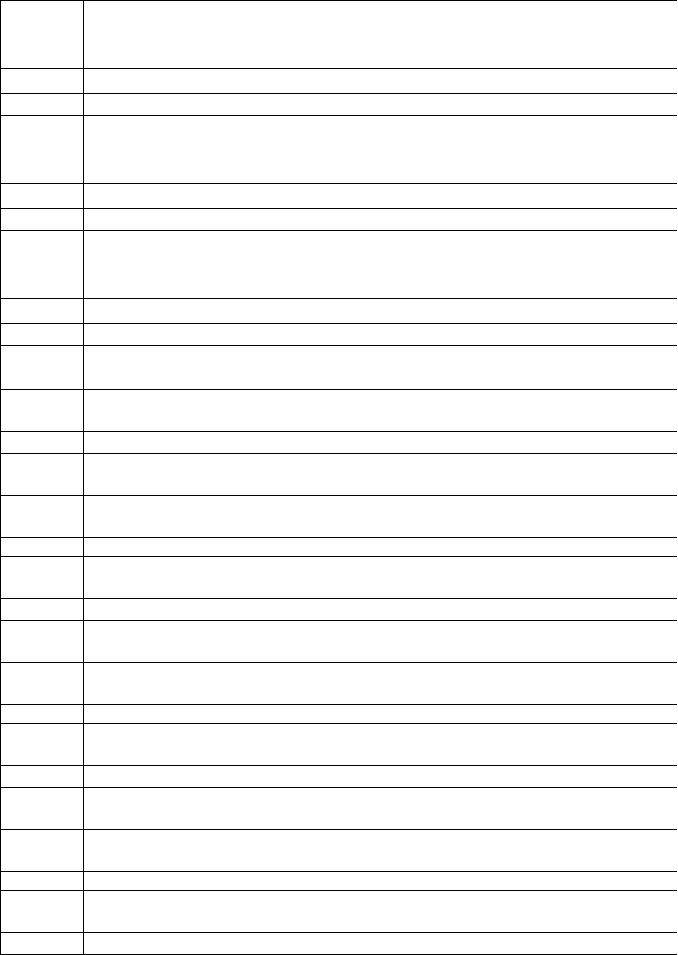
A |
1,38×10−23 Дж / К |
||||
В1 |
Число Лошмидта равно |
||||
A |
6,02 ×1023 моль−1 , |
||||
A+ |
2,69×1025 м−3 , |
||||
A |
8,31 Дж /(К × моль) , |
||||
A |
1,38×10−23 Дж / К |
||||
В1 |
Универсальная газовая постоянная равна |
||||
A |
6,02 ×1023 моль−1 , |
||||
A |
2,69×1025 м−3 , |
||||
A+ |
8,31 Дж /(К × моль) , |
||||
A |
1,38×10−23 Дж / К |
||||
В1 |
Постоянная Больцмана равна |
||||
A |
6,02 ×1023 моль−1 , |
||||
A |
2,69×1025 м−3 , |
||||
A |
8,31 Дж /(К × моль) , |
||||
A+ |
1,38×10−23 Дж / К |
||||
В1 |
Уравнение Менделеева-Клайперона имеет вид |
||||
A+ |
|
pV = |
m |
RT , |
|
|
|||||
|
|
|
|
M |
|
A |
|
pV = const , |
|||
A |
V |
= const , |
|||
|
|
T |
|
|
|
A |
|
p |
= const |
||
|
T |
||||
|
|
|
|
|
|
В1 |
Закон Бойля-Мариотта имеет вид |
||||
A |
|
pV = |
m |
RT , |
|
|
|
||||
|
|
|
|
M |
|
A+ |
|
pV = const , |
|||
A |
V |
= const , |
|||
|
|
T |
|
|
|
A |
|
p |
= const |
||
|
T |
||||
|
|
|
|
|
|
В1 |
Закон Гей-Люссака имеет вид |
||||
A |
|
pV = |
m |
RT , |
|
|
|
||||
|
|
|
|
M |
|
A |
|
pV = const , |
|||
A+ |
V |
= const , |
|||
|
|
T |
|
|
|
A |
|
p |
= const |
||
|
T |
||||
|
|
|
|
|
|
В1 |
Закон Шарля имеет вид |
||||
A |
|
pV = |
m |
RT , |
|
|
|
||||
|
|
|
|
M |
|
A |
|
pV = const , |
|||
22

A |
V |
|
= const , |
|||
|
|
T |
|
|
|
|
A+ |
|
p |
|
= const |
||
|
T |
|
||||
|
|
|
|
|
|
|
В1 |
Уравнение изотермы имеет вид |
|||||
A+ |
|
pV = const , T = const , m = const , |
||||
A |
V |
|
= const , p = const , m = const , |
|||
|
|
T |
|
|
|
|
A |
|
p |
|
= const V = const , m = const , |
||
|
T |
|
||||
|
|
|
|
|
|
|
A |
|
pV γ = const |
||||
В1 |
Уравнение изобары имеет вид |
|||||
A |
|
pV = const , T = const , m = const , |
||||
A+ |
V |
|
= const , p = const , m = const , |
|||
|
|
T |
|
|
|
|
A |
|
p |
|
= const V = const , m = const , |
||
|
T |
|
||||
|
|
|
|
|
|
|
A |
|
pV γ = const |
||||
В1 |
Уравнение изохоры имеет вид |
|||||
A |
|
pV = const , T = const , m = const , |
||||
A |
V |
|
= const , p = const , m = const , |
|||
|
|
T |
|
|
|
|
A+ |
|
p |
|
= const V = const , m = const , |
||
|
T |
|
||||
|
|
|
|
|
|
|
A |
|
pV γ = const |
||||
В1 |
Уравнение адиабаты имеет вид |
|||||
A |
|
pV = const , T = const , m = const , |
||||
A |
V |
|
= const , p = const , m = const , |
|||
|
|
T |
|
|
|
|
A |
|
p |
|
= const V = const , m = const , |
||
|
T |
|
||||
|
|
|
|
|
|
|
A+ |
|
pV γ = const |
||||
Т |
Классическая_статфизика |
|||||
|
|
|
|
|
|
|
В1 |
Средняя скорость молекул газа равна |
|||||
|
|
|
|
|
|
|
A+ |
|
|
8kT |
, |
||
|
|
|
|
π m |
|
|
|
|
|
|
|
|
|
A |
|
|
3kT |
, |
||
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
A |
|
|
2kT |
, |
||
|
|
|
|
m |
|
|
A |
0 |
|
|
|
|
|
В1 |
Средняя квадратичная скорость молекул газа равна |
|||||
|
|
|
|
|
||
A |
|
|
8kT |
, |
||
|
|
|
|
π m |
|
|
23

A+ |
|
|
3kT |
, |
|||
|
|
|
m |
|
|
|
|
|
|
|
|
, |
|||
A |
|
|
2kT |
||||
|
|
|
m |
|
|
|
|
A |
0 |
|
|
|
|
||
В1 |
Наиболее вероятная скорость молекул газа равна |
||||||
|
|
|
|
, |
|||
A |
|
|
8kT |
||||
|
|
|
π m |
||||
|
|
|
|
, |
|||
A |
|
|
3kT |
||||
|
|
|
m |
|
|
|
|
|
|
|
|
, |
|||
A+ |
|
|
2kT |
||||
|
|
|
m |
|
|
|
|
A |
0 |
|
|
|
|
||
В1 |
Средняя кинетическая энергия поступательного движения молекул равна |
||||||
A+ |
|
3 kT |
, |
|
|
||
|
2 |
|
|
|
|
||
A |
kT , |
|
|
|
|||
A |
|
i |
kT |
, |
|
|
|
2 |
|
|
|||||
|
|
|
|
|
|||
A |
|
1 kT |
|
|
|
||
|
2 |
|
|
|
|
||
В1 |
Наиболее вероятная кинетическая энергия поступательного движения отдельной |
||||||
молекулы равна |
|||||||
|
|||||||
A |
|
3 kT |
, |
|
|
||
|
2 |
|
|
|
|
||
A+ |
kT , |
|
|
|
|||
A |
|
i |
kT |
, |
|
|
|
2 |
|
|
|||||
|
|
|
|
|
|||
A |
|
1 kT |
|
|
|
||
|
2 |
|
|
|
|
||
В1 |
Средняя энергия молекулы равна |
||||||
A |
|
3 kT |
, |
|
|
||
|
2 |
|
|
|
|
||
A |
kT , |
|
|
|
|||
A+ |
|
i |
kT |
, |
|
|
|
2 |
|
|
|||||
|
|
|
|
|
|||
A |
|
1 kT |
|
|
|
||
|
2 |
|
|
|
|
||
В1 |
Средняя кинетическая энергия молекулы, приходящаяся на одну степень свободы, |
||||||
равна |
|||||||
|
|||||||
A |
|
3 kT |
, |
|
|
||
|
2 |
|
|
|
|
||
A |
kT , |
|
|
|
|||
A |
|
i |
kT |
, |
|
|
|
2 |
|
|
|||||
|
|
|
|
|
|||
24
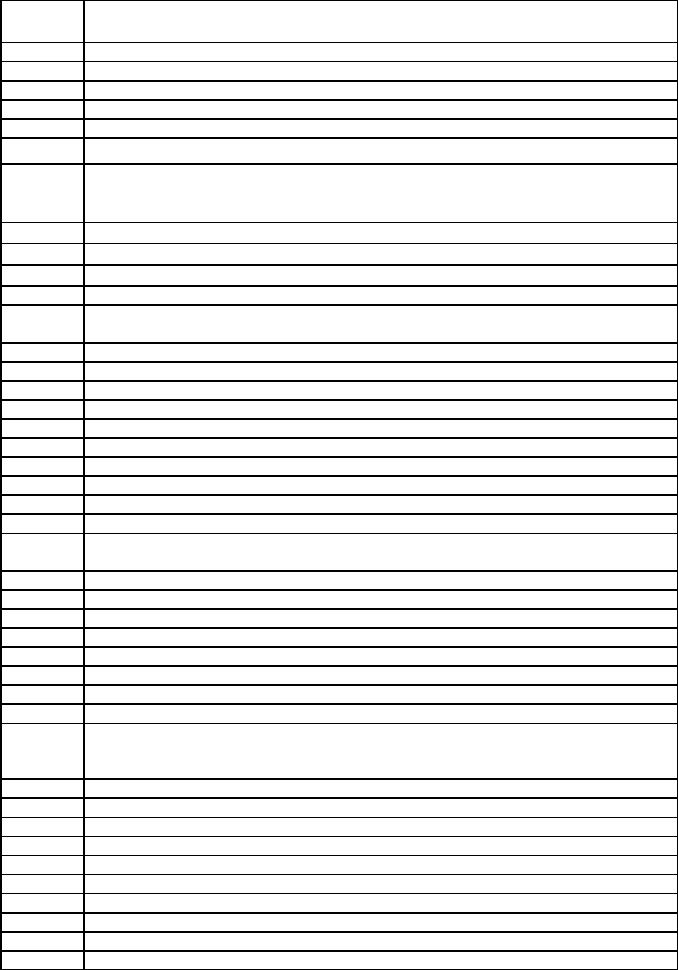
A+ |
1 kT |
|
|
2 |
|
В1 |
Внутренняя энергия идеального газа во время охлаждения |
|
A |
увеличивается; |
|
A+ |
уменьшается; |
|
A |
увеличивается или уменьшается в зависимости от объема; |
|
A |
не изменяется |
|
Т |
Термодинамика |
|
|
Над некоторой термодинамической системой внешние силы выполнили работу |
|
В1 |
δA′, количество теплоты, которую передали системе равняется δQ Изменение |
|
|
внутренней энергии системы равняется δU равняется |
|
A |
разности между работой δA′ и количеством теплоты δQ ; |
|
A |
разности между количеством теплоты δQ и работой δA′; |
|
A+ |
сумме работы δA′ и количества теплоты δQ ; |
|
A |
нулю |
|
В1 |
Концентрация частиц идеального газа не изменилась, а средняя кинетическая |
|
энергия теплового движения его молекул увеличилась в 3 раза Давление газа |
||
|
||
A+ |
увеличивается в 3 раза; |
|
A |
уменьшается в 3 раза; |
|
A |
не изменяется; |
|
A |
увеличивается в 9 раз |
|
В1 |
Работа, выполненная идеальным газом равняется нулю Какой это процесс? |
|
A |
изотермический; |
|
A |
адиабатический; |
|
A+ |
изохорный; |
|
A |
изобарный |
|
В1 |
Для изотермических процессов в идеальном газе |
|
A+ |
работа, выполненная идеальным газом, равняется количеству теплоты, полученной |
|
газом; |
||
|
||
A |
изменение внутренней энергии равняется количеству теплоты, полученной газом; |
|
A |
количество теплоты, полученное газом, равняется нулю; |
|
A |
изменение внутренней энергии газа равняется работе, выполненной газом |
|
В1 |
Чему равняется площадь заштрихованной на графике фигуры (рис1)? |
|
A |
изменению внутренней энергии системы; |
|
A |
работе, выполненной системой; |
|
A |
работе, выполненной над системой; |
|
A+ |
количеству теплоты, полученной системой |
|
|
В начальный момент времени некоторая изолированная термодинамическая |
|
В1 |
система не находится в состоянии равновесия Как с течением времени будет |
|
|
измеряется энтропия такой системы? |
|
A |
не будет изменятся; |
|
A |
уменьшится; |
|
A+ |
увеличится; |
|
A |
увеличится или уменьшится в зависимости от начальных параметров системы |
|
В1 |
Внутенняя энергия идеального газа зависит от |
|
A |
давления; |
|
A |
объема; |
|
A |
давления и объема; |
|
A+ |
температуры |
|
В1 |
Идеальный газ выполняет работу при |
25
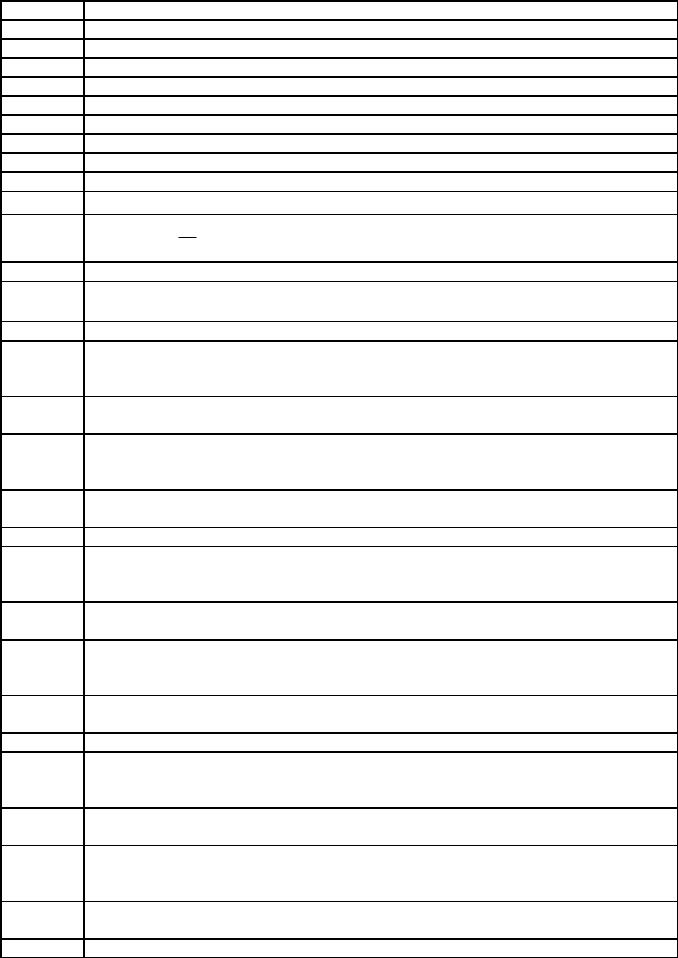
A+ |
изотермическом расширении; |
|
A |
изобарном сжатии; |
|
A |
изохорном процессе; |
|
A |
адиабатном сжатии |
|
В1 |
Адиабатный процесс – это процесс, |
|
A |
который происходит при постоянном давлении; |
|
A+ |
который происходит в теплоизолированной системе; |
|
A |
который происходит при постоянной температуре; |
|
A |
который происходит при постоянном объеме газа; |
|
В1 |
Работу для изотермического процесса в идеальном газе можно найти по формуле |
|
A |
A = p(V2 −V1 ) ; |
|
A+ |
m |
V2 |
A = μ RT ln |
V ; |
|
|
A = 0 ; |
1 |
A |
|
|
A |
A = − m CV |
T |
|
μ |
|
В1 |
Общее начало термодинамики утверждает, что |
|
|
вне зависимости от начального состояния изолированной термодинамической |
|
A+ |
системы в ней через некоторое конечное время всегда установится |
|
|
термодинамическое равновесие, |
|
Aколичество теплоты, сообщенное системе, равно сумме изменения ее внутренней энергии и работы, совершаемой системой над внешней средой, невозможен циклический процесс, единственным результатом которого было бы
Aпревращение теплоты, получаемой системой от внешней среды, в работу без изменений в окружающей среде,
Aвсе процессы при абсолютном нуле, при которых система переходит из одного равновесного состояния в другое, происходят без изменения энтропии
В1 |
Первое начало термодинамики утверждает, что |
|
вне зависимости от начального состояния изолированной термодинамической |
Aсистемы в ней через некоторое конечное время всегда установится термодинамическое равновесие,
A+ |
количество теплоты, сообщенное системе, равно сумме изменения ее внутренней |
|
энергии и работы, совершаемой системой над внешней средой, |
||
|
||
|
невозможен циклический процесс, единственным результатом которого было бы |
Aпревращение теплоты, получаемой системой от внешней среды, в работу без изменений в окружающей среде,
Aвсе процессы при абсолютном нуле, при которых система переходит из одного равновесного состояния в другое, происходят без изменения энтропии
В1 |
Второе начало термодинамики утверждает, что |
|
вне зависимости от начального состояния изолированной термодинамической |
Aсистемы в ней через некоторое конечное время всегда установится термодинамическое равновесие,
Aколичество теплоты, сообщенное системе, равно сумме изменения ее внутренней энергии и работы, совершаемой системой над внешней средой,
невозможен циклический процесс, единственным результатом которого было бы A+ превращение теплоты, получаемой системой от внешней среды, в работу без
изменений в окружающей среде,
Aвсе процессы при абсолютном нуле, при которых система переходит из одного равновесного состояния в другое, происходят без изменения энтропии
В1 |
Третье начало термодинамики утверждает, что |
26
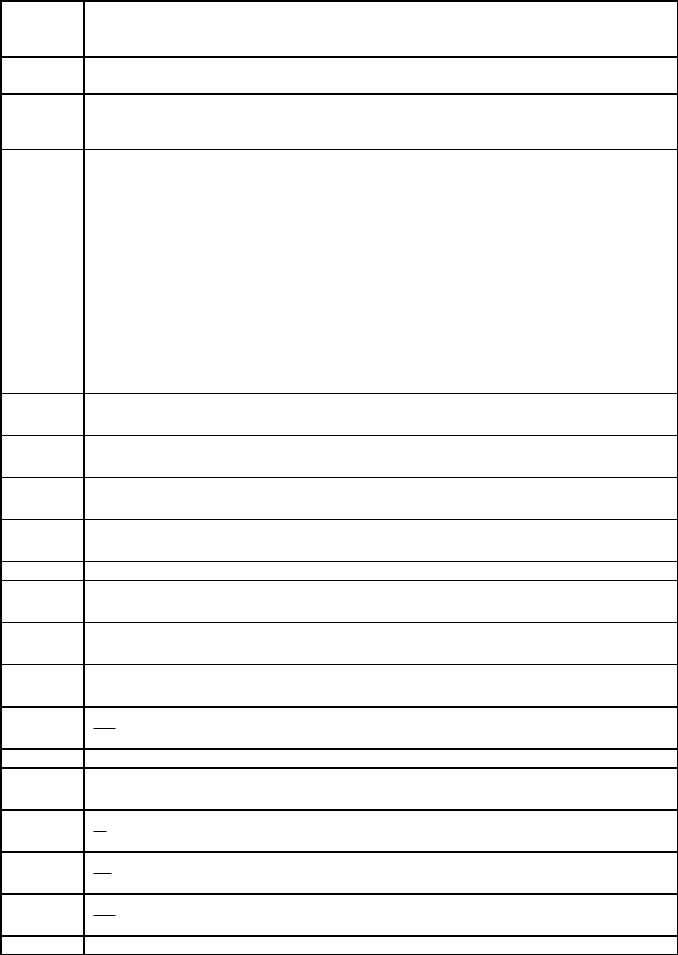
вне зависимости от начального состояния изолированной термодинамической
Aсистемы в ней через некоторое конечное время всегда установится термодинамическое равновесие,
Aколичество теплоты, сообщенное системе, равно сумме изменения ее внутренней энергии и работы, совершаемой системой над внешней средой, невозможен циклический процесс, единственным результатом которого было бы
Aпревращение теплоты, получаемой системой от внешней среды, в работу без изменений в окружающей среде,
A+ |
все процессы при абсолютном нуле, при которых система переходит из одного |
||||||
равновесного состояния в другое, происходят без изменения энтропии |
|||||||
|
|||||||
В1 |
Теплоемкость тела равна |
||||||
|
|
δ Q |
|
||||
A+ |
|
dT , |
|
||||
A |
|
1 δ Q |
, |
||||
|
m |
|
dT |
||||
A |
|
1 δ Q |
, |
||||
|
M |
|
dT |
||||
A |
|
Q |
|
|
|||
|
T |
|
|||||
|
|
|
|||||
В1 |
Удельная теплоемкость тела равна |
||||||
|
|
δ Q |
|
||||
A |
|
dT , |
|
||||
A+ |
|
1 δ Q |
, |
||||
|
m |
dT |
|||||
A |
|
1 δ Q |
, |
||||
|
M |
dT |
|||||
A |
|
Q |
|
|
|||
|
T |
|
|||||
|
|
|
|||||
В1 |
Молярная теплоемкость тела равна |
||||||
|
|
δ Q |
|
||||
A |
|
dT , |
|
||||
A |
|
1 δ Q |
, |
||||
|
m |
dT |
|||||
A+ |
|
1 δ Q |
, |
||||
|
M |
dT |
|||||
AQ
T
В1 |
Средняя теплоемкость тела равна |
|
|
δ Q |
|
A |
dT , |
|
A |
1 δ Q |
, |
m dT |
||
A |
1 δ Q |
, |
M dT |
||
A+ |
Q |
|
T |
|
|
|
|
|
В1 |
Количество теплоты, необходимое для нагревания тела массой m , равно |
|
27

A+ |
cm T , |
|
|
|
|
|
|
A |
rm , |
|
|
|
|
|
|
A |
λm , |
|
|
|
|
|
|
A |
qm , |
|
|
|
|
|
|
В1 |
Количество теплоты, необходимое для испарения тела массой m , равно |
||||||
A |
cm T , |
|
|
|
|
|
|
A+ |
rm , |
|
|
|
|
|
|
A |
λm , |
|
|
|
|
|
|
A |
qm , |
|
|
|
|
|
|
В1 |
Количество теплоты, выделяющееся при сгорании топлива массой m , равно |
||||||
A |
cm T , |
|
|
|
|
|
|
A |
rm , |
|
|
|
|
|
|
A+ |
λm , |
|
|
|
|
|
|
A |
qm , |
|
|
|
|
|
|
В1 |
При адиабатическом процессе |
||||||
A |
C = ∞ , n = 1 , |
pV = const , T = const , δ A = pdV , dU = 0 , dI = 0 , δ Q = δ A , |
|||||
A |
C = Cp |
, n = 0 , |
V |
= const , p = const , δ A = pdV , dU = CV dT , dI = δ Q = CpdT , |
|||
|
|
|
T |
|
|||
A |
C = CV |
, n = ∞ , |
p |
= const V = const , δ A = 0 , dU = CV dT = δ Q , dI = CpdT , |
|||
T |
|||||||
|
|
|
|
|
|||
A+ |
C = 0 , |
n = γ = |
Cp |
|
, pV γ = const , dU = CV dT = −δ A , dI = CpdT = −γδ A |
||
C |
|||||||
|
|
|
|
V |
|
||
В1 |
При изотермическом процессе |
||||||
A+ |
C = ∞ , n = 1 , |
pV = const , T = const , δ A = pdV , dU = 0 , dI = 0 , δ Q = δ A , |
|||||
A |
C = Cp |
, n = 0 , |
V |
= const , p = const , δ A = pdV , dU = CV dT , dI = δ Q = CpdT , |
|||
|
|
|
T |
|
|||
A |
C = CV |
, n = ∞ , |
p |
= const V = const , δ A = 0 , dU = CV dT = δ Q , dI = CpdT , |
|||
T |
|||||||
|
|
|
|
|
|||
A |
C = 0 , |
n = γ = |
Cp |
|
, pV γ = const , dU = CV dT = −δ A , dI = CpdT = −γδ A |
||
C |
|||||||
|
|
|
|
V |
|
||
В1 |
При изобарическом процессе |
||||||
A |
C = ∞ , n = 1 , |
pV = const , T = const , δ A = pdV , dU = 0 , dI = 0 , δ Q = δ A , |
|||||
A+ |
C = Cp |
, n = 0 , |
V |
= const , p = const , δ A = pdV , dU = CV dT , dI = δ Q = CpdT , |
|||
|
|
|
T |
|
|||
A |
C = CV |
, n = ∞ , |
p |
= const V = const , δ A = 0 , dU = CV dT = δ Q , dI = CpdT , |
|||
T |
|||||||
|
|
|
|
|
|||
A |
C = 0 , |
n = γ = |
Cp |
|
, pV γ = const , dU = CV dT = −δ A , dI = CpdT = −γδ A |
||
C |
|||||||
|
|
|
|
V |
|
||
В1 |
При изохорическом процессе |
||||||
A |
C = ∞ , n = 1 , |
pV = const , T = const , δ A = pdV , dU = 0 , dI = 0 , δ Q = δ A , |
|||||
A |
C = Cp |
, n = 0 , |
V |
= const , p = const , δ A = pdV , dU = CV dT , dI = δ Q = CpdT , |
|||
|
|
|
T |
|
|||
A+ |
C = CV |
, n = ∞ , |
p |
= const V = const , δ A = 0 , dU = CV dT = δ Q , dI = CpdT , |
|||
T |
|||||||
|
|
|
|
|
|||
A |
C = 0 , |
n = γ = |
Cp |
|
, pV γ = const , dU = CV dT = −δ A , dI = CpdT = −γδ A |
||
C |
|||||||
|
|
|
|
V |
|
||
28
Тест |
Физика_Электромагнетизм_(знания) |
|||||||||||||||||||||||
Т |
Электрическое_поле |
|||||||||||||||||||||||
В1 |
Закон сохранения электрического заряда определяется формулой: |
|||||||||||||||||||||||
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
A |
åqi |
= 0 ; |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
i=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
A+ |
åqi |
= const ; |
||||||||||||||||||||||
|
|
i=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
A |
|
d |
n |
|
q = const ; |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
dt åi=1 |
i |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
A |
ФE = |
|
|
|
1 åqi ; |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
εε0 |
|
|
i=1 |
|
|
|
|
|
|
||||||
В1 |
Сила воздействия двух неподвижных точечных зарядов, которая находится в |
|||||||||||||||||||||||
вакууме, определяется соотношением: |
||||||||||||||||||||||||
|
||||||||||||||||||||||||
A |
|
F = qE ; |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
r |
|
|
|
1 |
|
|
|
q1q2 r |
||||||||||||||
A+ |
|
F = |
|
|
|
|
|
|
|
|
|
; |
|
|
||||||||||
|
|
|
4πε0 |
|
r2 |
|
r |
|||||||||||||||||
|
|
r |
|
|
|
N |
r |
|
|
|
|
|
|
|
|
|
||||||||
A |
|
F = |
|
åFi |
; |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
i=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
r |
|
|
|
1 |
|
|
|
N |
q0qi rio |
|||||||||||||
A |
|
F = |
|
|
|
|
|
|
|
å r2 |
|
; |
||||||||||||
|
|
|
4πε |
0 |
|
|
r |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i=1 |
|
i0 i0 |
||||||||
В1 |
Результирующая сила F , с которой действуют на точечный заряд q N точечных |
|||||||||||||||||||||||
зарядов qi , где i =1,2,3,...N , определяется соотношением: |
||||||||||||||||||||||||
|
||||||||||||||||||||||||
|
|
|
|
|
N |
|
|
|
|
|
|
|
|
|
|
|||||||||
A+ |
|
F = |
|
å Fi |
; |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
i=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
N |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
A |
|
F = å Fi |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
i=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
A |
|
F = NFi ; |
|
|
|
|
|
|
|
|
|
|||||||||||||
A |
|
F = qE ; |
|
|
|
|
|
|
|
|
|
|||||||||||||
В1 |
Напряженность E электрического поля определяется формулой: |
|||||||||||||||||||||||
|
|
r |
|
|
|
N |
r |
|
|
|
|
|
|
|
|
|
||||||||
A |
|
E = |
|
Ei |
: |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
i=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
A |
|
E = −gradϕi ; |
||||||||||||||||||||||
|
|
r |
|
|
F |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
A+ |
|
E = |
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
q |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
r |
|
|
|
|
|
|
q |
|
|
|
r |
|||||||||||
A |
|
E = |
|
|
|
|
|
|
|
|
|
|
|
|
r |
|||||||||
|
|
|
4πε0εr |
3 |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
В1 |
Единицей измерения потока вектора напряженности электрического поля является: |
|||||||||||||||||||||||
A |
1 Клм ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
A |
1 Кл |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
м2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
A+ |
1 |
В |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
м |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
29
A |
1Ф ; |
||
В1 |
Поток вектора напряженности E электрического поля сквозь произвольную |
|
|
незамкнутую поверхность, помещенную в неоднородное поле, равен: |
|||
|
|||
A |
ФE = ES cosα ; |
|
|
A+ |
ФE = òS EdS ; |
||
A |
ФE = òS EdS ; |
||
A |
r |
|
|
ФE = (E,n)S ; |
|||
В1 |
Единицей измерения потока вектора напряженности электрического поля является: |
|
|
A+ |
1B × м ; |
|
|
A |
1Кл ; |
|
|
A |
1 Кл ; |
|
|
|
м3 |
||
A1 Кл
м2
В1 |
Потенциал электрического поля определяется соответствием: |
||||||||||||||||
A+ |
ϕ = |
|
П |
; |
|
|
|
|
|
|
|
|
|
||||
|
|
q |
|
|
|
|
|
|
|
|
|
|
|
||||
A |
ϕ = |
|
A |
; |
|
|
|
|
|
|
|
|
|
||||
|
q |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
N |
|
|
|
|
|
|
||||||
A |
ϕ = åϕi ; |
||||||||||||||||
|
|
|
|
i=1 |
|
|
|
|
|
|
|||||||
A |
ϕ = Ed |
|
|
|
|
|
|
|
|
|
|
||||||
В1 |
В общем случае потенциал связан с напряженностью электрического поля |
||||||||||||||||
соотношением: |
|||||||||||||||||
|
|||||||||||||||||
A+ |
E = −gradϕ ; |
||||||||||||||||
A |
E = |
|
ϕ1 −ϕ2 |
|
; |
|
|
|
|
|
|||||||
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
d |
|
|
|
|
|
|
||||
A |
E = − |
∂ϕ |
; |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
∂x |
|
|
|
|
|
|
||||||
A |
r |
|
|
r |
∂ϕ |
|
|
|
|
|
|
||||||
E = −i |
∂y |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
В1 |
Напряженность поля диполя в общем случае определяется формулой: |
||||||||||||||||
A |
E = |
|
|
|
|
|
P |
|
|
; |
|
|
|||||
|
|
2πεε0 r 3 |
|
|
|||||||||||||
|
|
|
|
|
|
|
P |
|
|
|
|
|
|||||
A+ |
E = |
|
|
|
|
|
|
|
1+ 3cos2 α ; |
||||||||
|
|
4πεε0 r |
3 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||
A |
E = |
|
|
|
|
M |
; |
|
|
|
|
|
|||||
|
P sinα |
|
|
|
|
|
|
||||||||||
A |
E = |
|
|
|
|
|
P |
|
|
|
|
|
|
||||
|
|
4πεε0 r3 |
|
||||||||||||||
В1 |
Линейная плотность заряда определяется выражением |
||||||||||||||||
|
dq |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A+ |
dl , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
30
