
answers (1)
.pdf
Тест |
Физика_Механика_(знания) |
|
|
Т |
Кинематика |
|
|
В1 |
Кинематика изучает |
|
|
A |
условия равновесия материальных тел под действием сил |
|
|
A+ |
геометрические законы движения тел без учета их масс и действующих на них сил |
|
|
A |
законы движения тел под действием приложенных к ним сил |
Aзаконы равновесия и перемещения одного тела относительно другого под действием сил
В2 |
Механика изучает |
|
A |
условия равновесия материальных тел под действием сил |
|
A |
геометрические законы движения тел без учета их масс и действующих на них сил |
|
A |
законы движения тел под действием приложенных к ним сил |
|
A+ |
законы равновесия и перемещения одного тела относительно другого под |
|
действием сил |
||
|
||
В3 |
Землю можно считать материальной точкой: |
|
A+ |
при изучении ее движения вокруг Солнца |
|
A |
при изучении ее вращательного движения вокруг своей оси |
|
A |
при изучении движения циклонов и антициклонов |
|
A |
при изучении движения литосферных плит |
|
В4 |
Системой отсчета называют: |
|
A+ |
тело или совокупность неподвижных тел, относительно которой определяется |
|
пространственное и временное положение других тел |
||
|
Aтройку линейно независимых направленных отрезков прямых, выходящих из одной точки
A |
тело, размерами которого можно пренебречь при описании его движения |
A |
совокупность тел, движение которых рассматривается |
В5 |
Системой координат называют:e |
Aтело или совокупность неподвижных тел, относительно которой определяется пространственное и временное положение других тел
A+ |
тройку линейно независимых направленных отрезков прямых, выходящих из одной |
|
точки |
||
|
||
A |
тело, размерами которого можно пренебречь при описании его движения |
|
A |
совокупность тел, движение которых рассматривается |
|
В6 |
Материальной точкой называют: |
Aтело или совокупность неподвижных тел, относительно которой определяется пространственное и временное положение других тел
Aтройку линейно независимых направленных отрезков прямых, выходящих из одной точки
A+ |
тело, размерами которого можно пренебречь при описании его движения |
A |
совокупность тел, движение которых рассматривается |
В7 |
Механической системой называют: |
Aтело или совокупность неподвижных тел, относительно которой определяется пространственное и временное положение других тел
Aтройку линейно независимых направленных отрезков прямых, выходящих из одной точки
A |
тело, размерами которого можно пренебречь при описании его движения |
A+ |
совокупность тел, движение которых рассматривается |
В8 |
Перемещением тела (материальной точки) называют: |
1
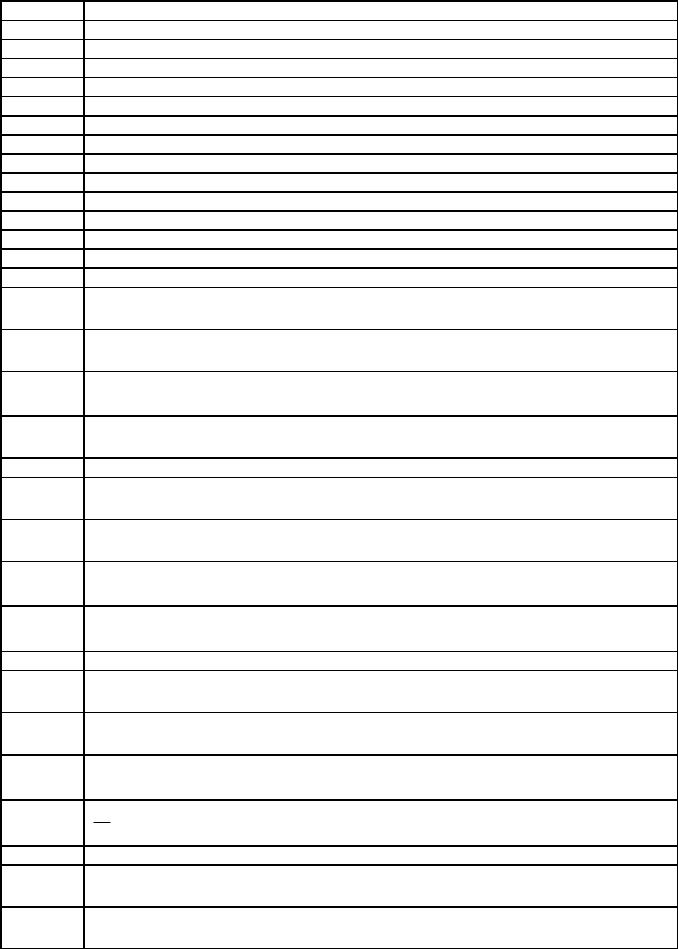
A+ |
вектор, проведенный из начальной точки движения тела в конечную |
|
A |
длину траектории |
|
A |
модуль вектора, проведенного из начальной точки движения тела в конечную |
|
A |
вектор, проведенный в данную точку из начала координат |
|
В9 |
Пройденным путем тела (материальной точки) называют: |
|
A |
вектор, проведенный из начальной точки движения тела в конечную |
|
A+ |
длину его траектории |
|
A |
модуль вектора, проведенного из начальной точки движения тела в конечную |
|
A |
вектор, проведенный в данную точку из начала координат |
|
В10 |
Радиус-вектором тела (материальной точки) называют: |
|
A |
вектор, проведенный из начальной точки движения тела в конечную |
|
A |
длину траектории |
|
A |
модуль вектора, проведенного из начальной точки движения тела в конечную |
|
A+ |
вектор, проведенный в данную точку из начала координат |
|
В11 |
Средняя скорость за промежуток времени |
t определяется выражением |
A+ |
r |
|
Dt |
|
|
|
|
|
A |
dr |
|
dt |
|
|
|
|
|
A |
d 2r |
|
dt2 |
|
|
|
|
|
A |
v |
|
Dt |
|
|
|
t определяется выражением |
|
В12 |
Среднее ускорение за промежуток времени |
|
A |
r |
|
Dt |
|
|
|
|
|
Adr dt
Ad 2r dt2
|
1 |
|
æ dr ö |
|
A+ |
|
|
|
D ç ÷ |
|
Dt |
|||
|
|
è dt ø |
||
В13 |
Мгновенная скорость определяется выражением |
|||
A |
|
r |
|
|
|
Dt |
|
||
|
|
|
||
A+ |
|
dr |
|
|
|
dt |
|
||
|
|
|
||
Ad 2r dt2
1 D æ dr ö
ADt çè dt ÷ø
В14 |
Мгновенное ускорение определяется выражением |
|
A |
r |
|
Dt |
||
|
Adr dt
2

A+ |
|
d 2r |
|
|
dt |
2 |
|
|
|
||
|
1 |
æ dr ö |
|
A |
|
|
D ç ÷ |
|
Dt |
||
|
|
è dt ø |
|
В15 |
Нормальное ускорение определяется выражением |
||
Adv dt
A+ |
v |
d æ v ö |
|
|
ç ÷ |
||
|
|||
|
|
dt è v ø |
|
Av dv v dt
Adv dt
В16 |
Тангенциальное ускорение определяется выражением |
|||
A |
dv |
|||
dt |
||||
|
||||
A |
v |
d æ v ö |
||
|
ç ÷ |
|||
|
||||
|
|
dt è v ø |
||
A+ |
v dv |
|||
v dt |
||||
|
||||
Adv dt
В17 |
Полное ускорение определяется выражением |
|||
A+ |
dv |
|||
dt |
||||
|
||||
A |
v |
d æ v ö |
||
|
ç ÷ |
|||
|
||||
|
|
dt è v ø |
||
Av dv v dt
Adv dt
В18 |
Математическое определение равномерного, прямолинейного движения является |
||||||
формула: |
|
||||||
|
|
||||||
A+ |
v = const |
|
|||||
A |
|
v |
|
|
|
= const |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
A |
a = const |
|
|||||
A |
|
a |
|
= const |
|
||
|
|
|
|||||
|
|
|
|
|
|
|
|
В19 |
При прямолинейном равномерном движении |
||||||
A+ |
v = const , v = const , a = 0 , an = 0 , aτ |
= 0 |
|||||
A |
v ¹ const , v = const , a = an , an ¹ 0 , aτ |
= 0 |
|||||
A |
v ¹ const , v ¹ const , a = aτ , an = 0 , aτ |
¹ 0 |
|||||
A |
v ¹ const , v ¹ const , a = an + aτ , an ¹ 0 , aτ ¹ 0 |
||||||
В20 |
При криволинейном равномерном движении |
||||||
A |
v = const , v = const , a = 0 , an = 0 , aτ |
= 0 |
|||||
3

A+ |
v ¹ const , v = const , a = an , an ¹ 0 , aτ |
= 0 |
|
|
|
|
|
|
||||||||||||
A |
v ¹ const , v ¹ const , a = aτ , an = 0 , aτ |
¹ 0 |
|
|
|
|
|
|
||||||||||||
A |
v ¹ const , v ¹ const , a = an + aτ , an ¹ 0 , aτ ¹ 0 |
|
|
|
|
|
|
|||||||||||||
В21 |
При прямолинейном неравномерном движении |
|
|
|
|
|
|
|||||||||||||
A |
v = const , v = const , a = 0 , an = 0 , aτ |
= 0 |
|
|
|
|
|
|
||||||||||||
A |
v ¹ const , v = const , a = an , an ¹ 0 , aτ |
= 0 |
|
|
|
|
|
|
||||||||||||
A+ |
v ¹ const , v ¹ const , a = aτ , an = 0 , aτ |
¹ 0 |
|
|
|
|
|
|
||||||||||||
A |
v ¹ const , v ¹ const , a = an + aτ , an ¹ 0 , aτ ¹ 0 |
|
|
|
|
|
|
|||||||||||||
В22 |
При криволинейном неравномерном движении |
|
|
|
|
|
|
|||||||||||||
A |
v = const , v = const , a = 0 , an = 0 , aτ |
= 0 |
|
|
|
|
|
|
||||||||||||
A |
v ¹ const , v = const , a = an , an ¹ 0 , aτ |
= 0 |
|
|
|
|
|
|
||||||||||||
A |
v ¹ const , v ¹ const , a = aτ , an = 0 , aτ |
¹ 0 |
|
|
|
|
|
|
||||||||||||
A+ |
v ¹ const , v ¹ const , a = an + aτ , an ¹ 0 , aτ ¹ 0 |
|
|
|
|
|
|
|||||||||||||
В23 |
Средняя путевая скорость тела определяется по формуле: |
|
|
|||||||||||||||||
A |
v = ds |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
dr |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v = |
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
v = v1 + v2 + ... + vN |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
N |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A+ |
v = |
s1 + s2 + ...+ sN |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
t1 + t2 +...+ tN |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
В24 |
Уравнение траектории материальной точки при равномерном прямолинейном |
|||||||||||||||||||
движении имеет вид: |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
A+ |
r (t) = r (t0 ) + v(t - t0 ) |
|
|
|
|
|
|
|
|
|
|
|
||||||||
A |
r |
r |
r |
(t0 )(t |
- t0 ) + |
a |
(t - t0 ) |
2 |
|
|
|
|
|
|
|
|||||
r (t) |
= r |
(t0 ) + v |
2 |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
r (t) = R(i cos(ω(t - t0 ) +ϕ(t0 )) + j sin(ω(t - t0 ) +ϕ(t0 ))) |
|
|
|
|
|||||||||||||||
|
r |
|
æ r |
æ |
β |
|
|
|
2 |
|
|
|
ö |
r |
æ |
β |
|
2 |
öö |
|
A |
r (t) |
= R ç i cos |
ç |
|
(t - t0 ) |
|
+ω(t0 )(t - t0 ) +ϕ(t0 )÷ + |
j sin ç |
|
(t - t0 ) |
|
+ω(t0 )(t - t0 ) +ϕ(t0 ) ÷÷ |
||||||||
2 |
|
2 |
|
|||||||||||||||||
|
|
|
|
è |
è |
|
|
|
|
|
|
|
ø |
|
è |
|
|
øø |
||
В25 |
Уравнение траектории материальной точки при равноускоренном прямолинейном |
|||||||||||||||||||
движении имеет вид: |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
A |
r (t) = r (t0 ) + v(t - t0 ) |
|
|
|
|
|
|
|
|
|
|
|
||||||||
A+ |
r |
r |
r |
(t0 )(t |
- t0 ) + |
a |
(t - t0 ) |
2 |
|
|
|
|
|
|
|
|||||
r (t) |
= r |
(t0 ) + v |
2 |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
r (t) = R(i cos(ω(t - t0 ) +ϕ(t0 )) + j sin(ω(t - t0 ) +ϕ(t0 ))) |
|
|
|
|
|||||||||||||||
|
r |
|
æ r |
æ |
β |
|
|
|
2 |
|
|
|
ö |
r |
æ |
β |
|
2 |
öö |
|
A |
r (t) |
= R ç i cos |
ç |
|
(t - t0 ) |
|
+ω(t0 )(t - t0 ) +ϕ(t0 )÷ + |
j sin ç |
|
(t - t0 ) |
|
+ω(t0 )(t - t0 ) +ϕ(t0 ) ÷÷ |
||||||||
2 |
|
2 |
|
|||||||||||||||||
|
|
|
|
è |
è |
|
|
|
|
|
|
|
ø |
|
è |
|
|
øø |
||
В26 |
Уравнение траектории материальной точки при равномерном движении по |
|||||||||||||||||||
окружности имеет вид: |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
A |
r (t) = r (t0 ) + v(t - t0 ) |
|
|
|
|
|
|
|
|
|
|
|
||||||||
A |
r |
r |
r |
(t0 )(t |
- t0 ) + |
a |
(t - t0 ) |
2 |
|
|
|
|
|
|
|
|||||
r (t) |
= r |
(t0 ) + v |
2 |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4
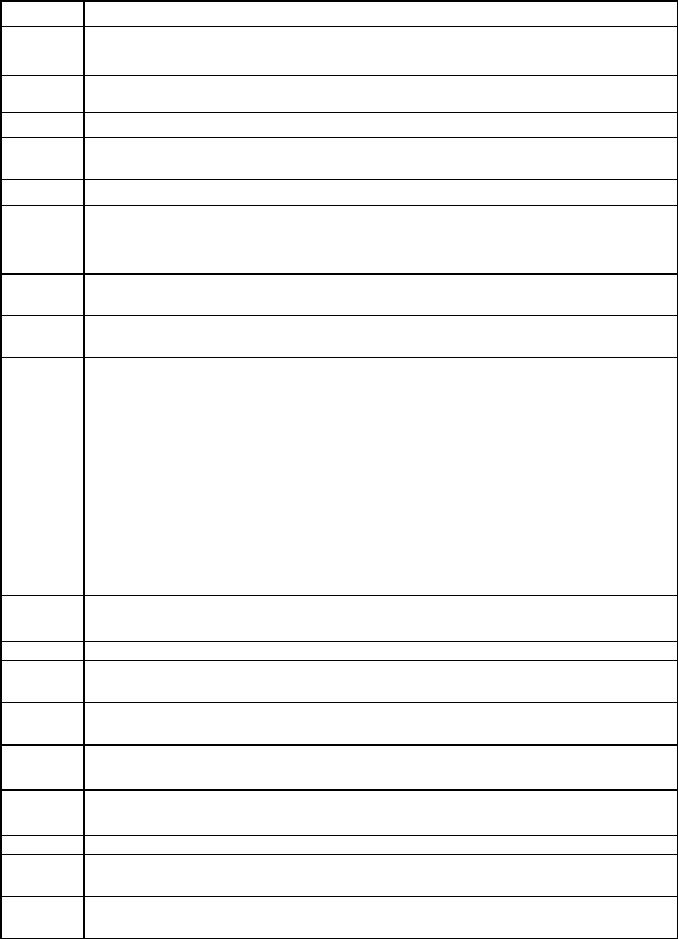
A+ |
r (t) = R(i cos(ω(t - t0 ) +ϕ(t0 )) + j sin(ω(t - t0 ) +ϕ(t0 ))) |
|
|
|
|
||||||||||
|
r |
æ r |
æ |
β |
|
2 |
|
|
ö |
r |
æ |
β |
|
2 |
öö |
A |
r |
(t) = R ç i |
cosç |
|
(t - t0 ) |
|
+ω(t0 )(t |
- t0 ) +ϕ(t0 )÷ |
+ j sin ç |
|
(t - t0 ) |
|
+ω(t0 )(t - t0 ) +ϕ(t0 ) ÷÷ |
||
2 |
|
2 |
|
||||||||||||
|
|
è |
è |
|
|
|
|
ø |
|
è |
|
|
øø |
||
В27 |
Уравнение траектории материальной точки при равноускоренном движении по |
||||||||||||||
окружности имеет вид: |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|||||
A |
r (t) = r (t0 ) + v(t - t0 ) |
|
|
|
|
|
|
|
|
|
|
||||
A |
r |
r |
r |
|
|
|
a |
(t - t0 ) |
2 |
|
|
|
|
|
|
r |
(t) = r (t0 ) + v(t0 )(t - t0 ) + |
2 |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
r (t) = R(i cos(ω(t - t0 ) +ϕ(t0 )) + j sin(ω(t - t0 ) +ϕ(t0 ))) |
|
|
|
|
||||||||||
|
r |
æ r |
æ |
β |
|
2 |
|
|
ö |
r |
æ |
β |
|
2 |
öö |
A+ |
r |
(t) = R ç i |
cosç |
|
(t - t0 ) |
|
+ω(t0 )(t |
- t0 ) +ϕ(t0 )÷ |
+ j sin ç |
|
(t - t0 ) |
|
+ω(t0 )(t - t0 ) +ϕ(t0 ) ÷÷ |
||
2 |
|
2 |
|
||||||||||||
|
|
è |
è |
|
|
|
|
ø |
|
è |
|
|
øø |
||
В28 |
Средняя угловая скорость определяется выражением: |
|
|
|
|||||||||||
Adϕ dt
A+ |
|
ϕ |
|
|
|
Dt |
|
||
|
|
|
||
A |
|
d 2ϕ |
|
|
|
dt |
2 |
|
|
|
|
|
||
|
1 |
æ dϕ ö |
||
A |
|
|
D ç |
÷ |
|
Dt |
|||
|
|
è |
dt ø |
|
В29 |
Мгновенная угловая скорость определяется выражением: |
|||
A+ |
|
dϕ |
|
|
|
dt |
|
|
|
|
|
|
|
|
A |
|
ϕ |
|
|
|
Dt |
|
||
|
|
|
||
A |
|
d 2ϕ |
|
|
|
dt |
2 |
|
|
|
|
|
||
|
1 |
æ dϕ ö |
||
A |
|
|
D ç |
÷ |
|
Dt |
|||
|
|
è |
dt ø |
|
В30 |
Среднее угловое ускорение определяется выражением: |
|||
A |
|
dϕ |
|
|
|
dt |
|
|
|
|
|
|
|
|
A |
|
ϕ |
|
|
|
Dt |
|
||
|
|
|
||
Ad 2ϕ dt2
|
1 |
|
æ dϕ ö |
||
A+ |
|
|
|
D ç |
÷ |
|
Dt |
||||
|
|
è |
dt ø |
||
В31 |
Мгновенное угловое ускорение определяется выражением: |
||||
A |
|
dϕ |
|
|
|
|
dt |
|
|
||
|
|
|
|
||
A |
|
ϕ |
|
||
|
Dt |
|
|
||
|
|
|
|
||
5
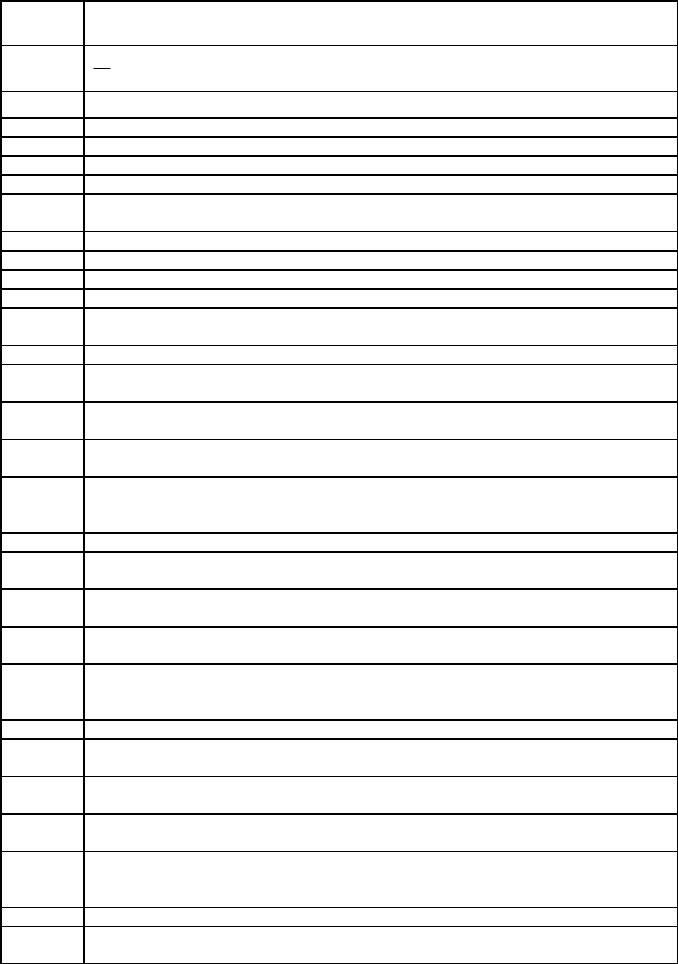
A+ |
d 2ϕ |
|
|
|
dt2 |
|
|
||
|
æ dϕ ö |
|||
A |
1 |
|
||
Dt |
D ç |
÷ |
||
|
|
è dt |
ø |
|
Т |
Динамика_поступательного_движения_ |
|||
В32 |
Динамика изучает |
|||
A |
условия равновесия материальных тел под действием сил |
|||
A |
геометрические законы движения тел без учета их масс и действующих на них сил |
|||
A+ |
законы движения тел под действием приложенных к ним сил |
|||
Aзаконы равновесия и перемещения одного тела относительно другого под действием сил
В33 |
Статика изучает |
A+ |
условия равновесия материальных тел под действием сил |
A |
геометрические законы движения тел без учета их масс и действующих на них сил |
A |
законы движения тел под действием приложенных к ним сил |
Aзаконы равновесия и перемещения одного тела относительно другого под действием сил
В34 |
Первый закон Ньютона утверждает, что |
|
A+ |
тело находится в состоянии покоя или равномерного прямолинейного движения, |
|
если оно не подвержено внешним воздействиям со стороны других тел |
||
|
Aускорение тела прямо пропорционально действующей силе и обратно пропорционально массе тел
Aсилы, с которыми действуют одно на другое взаимодействующие тела, равны по величине и противоположны по направлению сила, с которой две материальные точки притягивают одна другую, прямо
Aпропорциональна массам этих точек и обратно пропорциональна квадрату расстояния между ними
В35 |
Второй закон Ньютона утверждает, что |
Aтело находится в состоянии покоя или равномерного прямолинейного движения, если оно не подвержено внешним воздействиям со стороны других тел
A+ |
ускорение тела прямо пропорционально действующей силе и обратно |
|
пропорционально массе тел |
||
|
Aсилы, с которыми действуют одно на другое взаимодействующие тела, равны по величине и противоположны по направлению сила, с которой две материальные точки притягивают одна другую, прямо
Aпропорциональна массам этих точек и обратно пропорциональна квадрату расстояния между ними
В36 |
Третий закон Ньютона утверждает, что |
Aтело находится в состоянии покоя или равномерного прямолинейного движения, если оно не подвержено внешним воздействиям со стороны других тел
Aускорение тела прямо пропорционально действующей силе и обратно пропорционально массе тел
A+ |
силы, с которыми действуют одно на другое взаимодействующие тела, равны по |
|
величине и противоположны по направлению |
||
|
||
|
сила, с которой две материальные точки притягивают одна другую, прямо |
Aпропорциональна массам этих точек и обратно пропорциональна квадрату расстояния между ними
В37 |
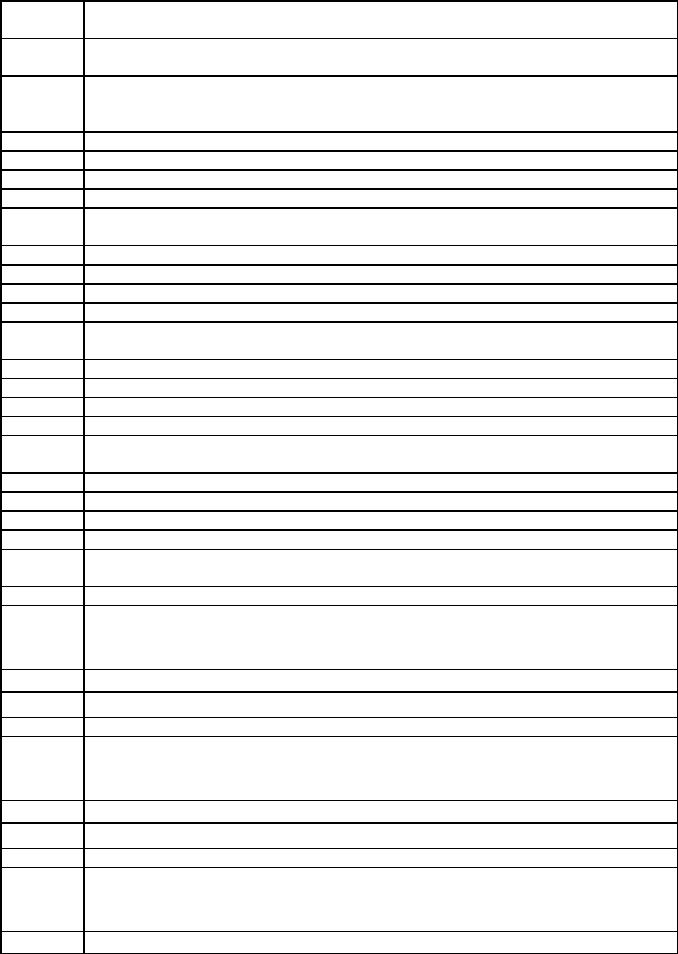
Закон всемирного тяготения утверждает, что |
Aтело находится в состоянии покоя или равномерного прямолинейного движения, если оно не подвержено внешним воздействиям со стороны других тел
6
Aускорение тела прямо пропорционально действующей силе и обратно пропорционально массе тел
Aсилы, с которыми действуют одно на другое взаимодействующие тела, равны по величине и противоположны по направлению
|
сила, с которой две материальные точки притягивают одна другую, прямо |
|
A+ |
пропорциональна массам этих точек и обратно пропорциональна квадрату |
|
|
расстояния между ними |
|
В38 |
Слабое взаимодействие происходит между |
|
A |
телами, имеющими массу |
|
A |
телами или частицами, обладающими электрическими зарядами |
|
A |
элементарными частицами, называемыми адронами |
|
A+ |
элементарными частицами при превращении некоторых элементарных частиц и |
|
атомных ядер |
||
|
||
В39 |
Гравитационное взаимодействие происходит между |
|
A+ |
телами, имеющими массу |
|
A |
телами или частицами, обладающими электрическими зарядами |
|
A |
элементарными частицами, называемыми адронами |
Aэлементарными частицами при превращении некоторых элементарных частиц и атомных ядер
В40 |
Электромагнитное взаимодействие происходит между |
A |
телами, имеющими массу |
A+ |
телами или частицами, обладающими электрическими зарядами |
A |
элементарными частицами, называемыми адронами |
Aэлементарными частицами при превращении некоторых элементарных частиц и атомных ядер
В41 |
Сильное взаимодействие происходит между |
A |
телами, имеющими массу |
A |
телами или частицами, обладающими электрическими зарядами |
A+ |
элементарными частицами, называемыми адронами |
Aэлементарными частицами при превращении некоторых элементарных частиц и атомных ядер
В42 |
Какая формула из приведенных ниже соответствует силе трения? |
||
A |
r |
2 |
r |
F = − mv |
|
||
|
R |
|
r |
A |
F = −kx |
|
|
A+ |
F = μ N |
|
|
A |
r |
|
|
F = mg |
|
|
|
В42 |
Какая формула из приведенных ниже соответствует силе гравитации? |
||
A |
r |
2 |
r |
F = − mv |
|
||
|
R |
|
r |
A |
F = −kx |
|
|
A |
F = μ N |
|
|
A+ |
r |
|
|
F = mg |
|
|
|
В42 |
Какая формула из приведенных ниже соответствует силе упругости? |
||
A |
r |
2 |
r |
F = − mv |
|
||
|
R |
|
r |
A+ |
F = −kx |
|
|
A |
F = μ N |
|
|
7

A |
F |
|
r |
||
= mg |
|||||
В43 |
Какая формула из приведенных ниже описывает основной закон динамики? |
||||
A |
F |
t |
|||
A |
åFi |
||||
|
i |
|
|
|
|
A+ |
r |
|
|
|
|
F = dp |
|||||
|
|
|
dt |
||
|
r |
|
åmi ri |
||
|
|
i |
|||
A |
rc |
= |
|
|
|
åmi |
|||||
|
|
|
i |
||
В44 |
Какая формула из приведенных ниже описывает импульс силы? |
||||
A+ |
F |
t |
|||
A |
åFi |
||||
|
i |
|
|
|
|
A |
r |
|
|
|
|
F = dp |
|||||
|
|
|
dt |
||
|
r |
|
åmi ri |
||
|
|
i |
|||
A |
rc |
= |
|
|
|
åmi |
|||||
|
|
|
i |
||
В45 |
Какая формула из приведенных ниже описывает результирующую нескольких сил? |
||||
A |
F |
t |
|||
A+ |
åFi |
||||
|
i |
|
|
|
|
A |
r |
|
|
|
|
F = dp |
|||||
|
|
|
dt |
||
|
r |
|
åmi ri |
||
|
|
i |
|||
A |
rc |
= |
|
|
|
åmi |
|||||
|
|
|
i |
||
В46 |
Для замкнутой системы материальных точек закон сохранения полного импульса |
||||
задается выражением: |
|||||
|
|||||
A+ |
r |
|
N r |
||
p |
= å pi = const |
||||
|
|
|
i=1 |
||
|
r |
|
N r |
||
A |
L |
= åLi = const |
|||
|
|
|
i=1 |
||
|
|
|
N |
||
A |
M = åmi = const |
||||
|
|
|
i=1 |
||
|
|
|
N |
||
A |
E = å(Ti +Ui ) = const |
||||
|
|
|
i=1 |
||
В47 |
Для замкнутой системы материальных точек закон сохранения масс задается |
||||
выражением: |
|||||
|
|||||
A |
r |
|
N r |
||
p |
= å pi = const |
||||
|
|
|
i=1 |
||
|
r |
|
N r |
||
A |
L |
= åLi = const |
|||
|
|
|
i=1 |
||
8

|
|
N |
|
|
A+ |
M = åmi = const |
|||
|
|
i=1 |
|
|
|
|
N |
|
|
A |
E = å(Ti +Ui ) = const |
|||
|
|
i=1 |
|
|
Т |
Работа_и_энергия |
|||
|
|
|||
В48 |
Какая формула из приведенных ниже выражает работу при бесконечно малом |
|||
перемещении? |
||||
|
||||
|
r2 r |
r |
|
|
A |
ò Fdr |
|
||
|
r1 |
|
|
|
A+ |
r |
|
|
|
Fdr |
|
|
||
A |
ò Fdl |
|
||
|
L |
|
|
|
A |
F = −gradU |
|||
|
|
|||
В49 |
Какая формула из приведенных ниже выражает связь силы и потенциальной |
|||
энергии? |
|
|||
|
|
|||
|
r2 r |
r |
|
|
A |
ò Fdr |
|
||
|
r1 |
|
|
|
A |
r |
|
|
|
Fdr |
|
|
||
A |
ò |
|
|
|
|
Fdl |
|
||
|
L |
|
|
|
A+ |
F = −gradU |
|||
|
|
|||
В50 |
Какая формула из приведенных ниже выражает работу изменяющейся в |
|||
пространстве силы? |
||||
|
||||
|
r2 r |
r |
|
|
A+ |
ò Fdr |
|
||
|
r1 |
|
|
|
A |
r |
|
|
|
Fdr |
|
|
||
A |
ò |
|
|
|
|
Fdl |
|
||
|
L |
|
|
|
A |
F = −gradU |
|||
|
|
|||
В51 |
Какая формула из приведенных ниже выражает циркуляцию силы? |
|||
|
r2 r |
r |
|
|
A |
ò Fdr |
|
||
|
r1 |
|
|
|
A |
r |
|
|
|
Fdr |
|
|
||
A+ |
ò |
|
|
|
|
Fdl |
|
||
|
L |
|
|
|
A |
F = −gradU |
|||
|
|
|||
В52 |
Для замкнутой системы невзаимодействующих материальных точек закон |
|||
сохранения полной механической энергии задается выражением: |
||||
|
||||
A |
r |
N r |
= const |
|
p = |
å pi |
|||
|
|
i=1 |
|
|
|
r |
N r |
|
|
A |
L = |
åLi |
= const |
|
|
|
i=1 |
|
|
9
|
|
|
|
|
N |
|
|
|
A |
|
M = åmi = const |
||||||
|
|
|
|
|
i=1 |
|
|
|
|
|
|
|
|
N |
|
|
|
A+ |
|
E = å(Ti |
+Ui ) = const |
|||||
|
|
|
|
|
i=1 |
|
|
|
В53 |
Элементарная работа силы определяется выражением |
|||||||
A+ |
|
|
|
r |
|
|
|
|
|
Fdr |
|
|
|
||||
|
1 |
|
|
æ |
r |
r ö |
||
A |
|
|
|
D ç ò Fdr ÷ |
||||
|
Dt |
|||||||
|
|
|
è L |
|
ø |
|||
|
|
d |
æ |
r |
r |
ö |
||
A |
|
|
|
ç |
ò Fdr |
÷ |
||
|
dt |
|||||||
|
|
è |
L |
|
ø |
|||
A |
|
|
|
|
r |
|
|
|
|
ò Fdr |
|
|
|||||
|
|
L |
|
|
|
|
||
В54 |
Работа силы вдоль криволинейной траектории определяется выражением |
|||||||
A |
|
|
|
r |
|
|
|
|
|
Fdr |
|
|
|
||||
|
1 |
|
|
æ |
r |
r ö |
||
A |
|
|
|
D ç ò Fdr ÷ |
||||
|
Dt |
|||||||
|
|
|
è L |
|
ø |
|||
|
|
d |
æ |
r |
r |
ö |
||
A |
|
|
|
ç |
ò Fdr |
÷ |
||
|
dt |
|||||||
|
|
è |
L |
|
ø |
|||
A+ |
|
|
|
|
r |
|
|
|
|
ò Fdr |
|
|
|||||
|
|
L |
|
|
|
|
||
В55 |
Мгновенная мощность силы определяется выражением |
|||||||
A |
|
|
|
r |
|
|
|
|
|
Fdr |
|
|
|
||||
|
1 |
|
|
æ |
r |
r ö |
||
A |
|
|
|
D ç ò Fdr ÷ |
||||
|
Dt |
|||||||
|
|
|
è L |
|
ø |
|||
|
|
d |
æ |
r |
r |
ö |
||
A+ |
|
|
|
ç |
ò Fdr |
÷ |
||
|
dt |
|||||||
|
|
è |
L |
|
ø |
|||
A |
|
|
|
|
r |
|
|
|
|
ò Fdr |
|
|
|||||
|
|
L |
|
|
|
|
||
В56 |
Средняя мощность силы за некоторый промежуток времени определяется |
|||||||
выражением |
||||||||
|
||||||||
A |
|
|
|
r |
|
|
|
|
|
Fdr |
|
|
|
||||
|
1 |
|
|
æ |
r |
r ö |
||
A+ |
|
|
|
D ç ò Fdr ÷ |
||||
|
Dt |
|||||||
|
|
|
è L |
|
ø |
|||
|
|
d |
æ |
r |
r |
ö |
||
A |
|
|
|
ç |
ò Fdr |
÷ |
||
|
dt |
|||||||
|
|
è |
L |
|
ø |
|||
A |
|
|
|
|
r |
|
|
|
|
ò Fdr |
|
|
|||||
|
|
L |
|
|
|
|
||
В57 |
Потенциальная энергия материальной точки в однородном поле тяготения имеет |
|||||||
величину |
|
|||||||
|
|
|||||||
A+ |
mgh |
|
|
|||||
A |
-G m1m2 |
|
||||||
|
|
|
|
|
r |
|
|
|
10
