
ман для 1ПМ-11 / 2 курс 2011 / лекции / Функції та їх границі / лекция № 8
.docxМіністерство освіти і науки, молоді та спорту України
Горлівський технікум Донецького національного університету
ЛЕКЦІЯ № 8
з теми: «Визначення границі функції. Умови її існування. Однобічні границі функції. Властивості границь.»
Модуль КЗН-02. ПР.О.03.03 Функції та їх границі
Дисципліна: «Математичний аналіз»
Розглянуто та схвалено Розробив викладач
на засіданні циклової Велікодна О. В.
комісії інформаційних технологій
та прикладної математики.
протокол № 1 від 30.08.2011 р.
Голова циклової
комісії ІТ та ПМ І. П. Сошина
ПЛАН ЗАНЯТТЯ
Дата: курс: ІІ
Викладач: Велікодна Ольга Володимирівна.
Тема: Визначення границі функції. Умови її існування. Однобічні границі функції. Властивості границь.
Мета:
-
Дидактична: вивчити основні визначення границі функції в точці та умови її існування, властивості границі функції в точці.
-
Виховна: виховувати професійно зацікавлену особистість, здатну вільно мислити та логічно висловлювати свої думки.
-
Методична: вдосконалювати методику проведення лекції з використанням технологій проблемного та проектного навчання.
Тип: лекція № 8
Вид: лекція – дослідження проблемних питань.
Методи та форми проведення заняття: метод проблемного викладення матеріалу, репродуктивний, дослідницький.
Науково-методичне забезпечення:
-
Кудрявцев Л.Д. Курс математического анализа: Учебник. Для студентов университетов и вузов. В 3 т. - М.: Высшая школа,1998.
-
Кудрявцев Л.Д. Сборник задач по математическому анализу: Учебник для вузов. В 3 т. - М.: Наука. Гл. ред. физ. - мат. лит.,1989.
-
Берман Г.Н. Сборник задач по курсу математического анализа: Учеб. пособие для вузов. - М.: Наука. Гл. ред. физ. - мат. лит.,1975.
-
Марон А. И. Дифференциальное и интегральное исчисление в примерах и задачах. – М.: Наука, 1973.
Між предметні зв’язки:
-
Дисципліни, що забезпечують: елементарна математика
-
Дисципліни, що забезпечуються: лінійна алгебра та аналітична геометрія, дискретна математика, диференціальні рівняння, рівняння математичної фізики, чисельні методи, методи оптимізації, теорія функцій комплексної змінної.
Обладнання: зошити, ручки, крейда, дошка.
ХІД ЗАНЯТТЯ.
-
Організаційна частина:
-
відсутні;
-
підготовка до заняття;
-
перевірка д/з.
-
Актуалізація опорних знань:
-
Вивчення нового матеріалу:
-
Тема лекції: Визначення границі функції. Умови її існування. Однобічні границі функції. Властивості границь.
-
Мотивація вивчення матеріалу: вивчити основне поняття математичного аналізу, яке дає можливість застосування апарату дослідження у будь – яких сферах прикладання математичних задач.
-
План вивчення нового матеріалу: надається в конспекті лекції.
-
Виклад нового матеріалу. Конспект лекції надається.
-
Закріплення нового матеріалу.
-
Підсумки заняття.
-
Домашнє завдання:
План лекції № 8.
-
Визначення границі функції в точці.
-
Умови існування границі функції в точці. Неперервність функції в точці.
-
Однобічні границі та однобічна неперервність функції в точці.
-
Властивості границі функції в точці.
Конспект лекції № 8.
Тема: «Визначення границі функції. Умови її існування. Однобічні границі функції. Властивості границь.»
-
Визначення 1.(по Гейне) Точка а називається границею значень функції ƒ(х), х
 Х,
в точці х
Х,
в точці х ,
якщо для будь – якої послідовності
точок х
,
якщо для будь – якої послідовності
точок х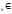 Х,
n = 1,2,…, границя якої є х
Х,
n = 1,2,…, границя якої є х ,
тобто
,
тобто
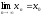 ,
послідовність {ƒ(х
,
послідовність {ƒ(х )}
значень функції ƒ(х) в точках х
)}
значень функції ƒ(х) в точках х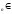 Х,
n = 1,2,…, має своєю границею точку а, тобто
Х,
n = 1,2,…, має своєю границею точку а, тобто
 .
.
За допомогою символів визначення записується таким чином:
 .
.
Якщо а
– число, то говорять, що функція ƒ(х) в
точці х має скінчену границю.
має скінчену границю.
Визначення
2.
Проколотою ε – окрестністю точки х Ů(х
Ů(х ,
ε) називається множина, що отримана
видаленням точки х
,
ε) називається множина, що отримана
видаленням точки х з її окрестності.
з її окрестності.
Приклади:
1).
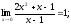
2).
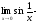 не
існує;
не
існує;
3).
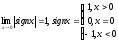 .
.
-
Якщо х

 Х
та існує
Х
та існує
 ,
то він дорівнює ƒ(х
,
то він дорівнює ƒ(х ),
тобто
),
тобто
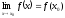 .
.
Визначення
3.
Якщо
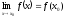 ,
то функція ƒ(х) називається неперервною
в точці х
,
то функція ƒ(х) називається неперервною
в точці х .
.
Лемма.
Для того, щоб функція ƒ(х), х Х,
мала скінчену чи деякого знаку нескінчену
границю в точці х
Х,
мала скінчену чи деякого знаку нескінчену
границю в точці х ,
необхідно та достатньо, щоб для будь –
якої послідовності точок х
,
необхідно та достатньо, щоб для будь –
якої послідовності точок х Х,
n = 1,2,…, границя якої є х
Х,
n = 1,2,…, границя якої є х ,
тобто
,
тобто
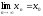 ,
послідовність {ƒ(х
,
послідовність {ƒ(х )}
відповідних значень функції мала границю
(скінчену чи визначеного знаку
нескінченості).
)}
відповідних значень функції мала границю
(скінчену чи визначеного знаку
нескінченості).
Доведення. Необхідність сформульованої умови для існування границі функції знаходиться у самому визначенні цього поняття.
Достатність.
Нехай
функція ƒ визначена в проколотому
околі точки
точки
 та нехай для будь-якої послідовності
та нехай для будь-якої послідовності
 з цього околу,
з цього околу,
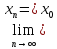 послідовність
послідовність
 ,
n = 1, 2, 3, …., збігається.
,
n = 1, 2, 3, …., збігається.
Розглянемо
дві підпослідовності
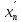 та
та
 в проколотому околі точки
в проколотому околі точки
 ,
такі, що
,
такі, що
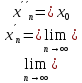 .
Тоді послідовність
.
Тоді послідовність
 ,
k = 1, 2, 3, … також збігається до точці
,
k = 1, 2, 3, … також збігається до точці
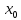 .
Відповідно до розглянутого, існують
границі
.
Відповідно до розглянутого, існують
границі
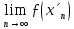 ,
,
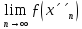 та
та
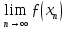 ,
причому послідовності
,
причому послідовності
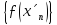 та
та
 є під послідовностями послідовності
є під послідовностями послідовності
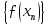 .
.
Згадаємо,
що якщо деяка послідовність має границю,
то будь-яка її підпослідовність має ту
ж саму границю. Тому
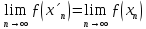 ,
,
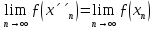 ,
та маємо, що
,
та маємо, що
 .
Таким чином, границі послідовностей
.
Таким чином, границі послідовностей
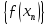 ,
де
,
де
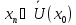 ,
n = 1, 2, 3, … та
,
n = 1, 2, 3, … та
 не залежать від вибору послідовності
не залежать від вибору послідовності
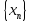 .
Позначаючи їх загальне значення через
а
відповідно до визначення границі по
Гейне будемо мати:
.
Позначаючи їх загальне значення через
а
відповідно до визначення границі по
Гейне будемо мати:
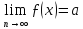
-
Визначення 5.(по Коші) Точка а називається границею значень функції ƒ(х), х
 Х,
при х → х
Х,
при х → х ,
якщо для будь – якого околу U(а) точки
а існує такий окіл точки х
,
якщо для будь – якого околу U(а) точки
а існує такий окіл точки х U(х
U(х ),
що ƒ(Х∩U(х
),
що ƒ(Х∩U(х ))
))
 U(а).
U(а).
За допомогою символів визначення записується таким чином:
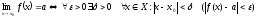 чи
за допомогою околів
чи
за допомогою околів
 .
.
Якщо границя функції нескінчена, при х → ± ∞, то визначення границі буде:
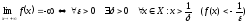 .
.
Теорема. Визначення границі функції в точці по Гейне та по Коші еквівалентні.
Доведення.
1. Нехай
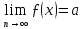 у сенсі визначення по Гейне. Тоді функція
ƒ визначена в деякім проколотому околі
у сенсі визначення по Гейне. Тоді функція
ƒ визначена в деякім проколотому околі
 точки
точки
 та для будь-якої послідовності
та для будь-якої послідовності
 ,
n = 1, 2, …,
,
n = 1, 2, …,
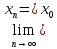 має місце
має місце
 .
покажемо, що виконується умова
.
покажемо, що виконується умова
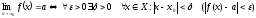 .
.
Припустимо,
що це не так, тобто
 .
Тобто існує таке
.
Тобто існує таке
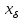 ,
вибір якого залежить від вибору δ, та
для якого буде виконана дана умова
,
вибір якого залежить від вибору δ, та
для якого буде виконана дана умова
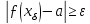 .
.
Будемо
послідовно обирати
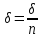 ,
n=1, 2, …, а відповідні
,
n=1, 2, …, а відповідні
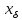 позначати через
позначати через
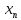 :
:
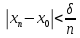 ,
,
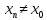 , n=1, 2, …, та маємо
, n=1, 2, …, та маємо
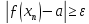 .
З отриманого слідує, що
.
З отриманого слідує, що
 та
та
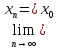 ,
але умова
,
але умова
 показує, що число a
не
може бути границею послідовності
показує, що число a
не
може бути границею послідовності
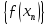 .
Це є протиріччям до визначення границі
по Гейне. Отримане протиріччя доводить
дане твердження.
.
Це є протиріччям до визначення границі
по Гейне. Отримане протиріччя доводить
дане твердження.
2. Нехай
тепер
 у сенсі визначення по Коші. Покажемо,
що тоді функція ƒ насамперед визначена
в деякім проколотому околі
у сенсі визначення по Коші. Покажемо,
що тоді функція ƒ насамперед визначена
в деякім проколотому околі
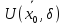 точки
точки
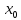 .
Наприклад, візьмемо ε = 1. Для нього
відповідно до визначення по Коші існує
таке
.
Наприклад, візьмемо ε = 1. Для нього
відповідно до визначення по Коші існує
таке
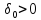 ,
що для всіх х
,
що для всіх х
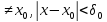 виконана умова
виконана умова
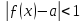 ,
та відповідно, для всіх таких значень
х визначена функція ƒ. Таким чином,
функція ƒ визначена в деякім проколотому
околі
,
та відповідно, для всіх таких значень
х визначена функція ƒ. Таким чином,
функція ƒ визначена в деякім проколотому
околі
 точки
точки
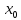 .
Візьмемо
.
Візьмемо
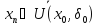 ,
n = 1, 2, …, та
,
n = 1, 2, …, та
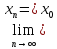 .
Покажемо, що якщо функція ƒ задовольняє
умовам визначення границі по Коші, то
.
Покажемо, що якщо функція ƒ задовольняє
умовам визначення границі по Коші, то
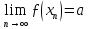 .
.
Перевіримо
це. Задамо довільно ε
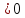 та оберемо для нього
та оберемо для нього
 .
Для цього
.
Для цього
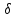 знайдеться
таке
знайдеться
таке
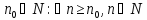 буде виконано нерівність
буде виконано нерівність
 .
З цієї ж умови маємо, що
.
З цієї ж умови маємо, що

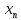
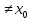 .
Тому для всіх
.
Тому для всіх
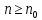 буде виконано, що
буде виконано, що
 .
Це й означає виконання зазначеної в
теоремі умови.
.
Це й означає виконання зазначеної в
теоремі умови.
-
Введемо наступні позначення:
 R
положимо
R
положимо
 ;
;
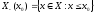 .
Якщо множина
.
Якщо множина
 не пуста, то х
не пуста, то х = inf
= inf
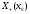 ;
якщо множина
;
якщо множина
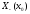 не пуста, то х
не пуста, то х = sup
= sup
 .
.
Визначення
6.
Нехай задана функція ƒ(х), х Х,
та х
Х,
та х R.
Точка а називається границею
значень функції
ƒ(х)
зліва
при х → х
R.
Точка а називається границею
значень функції
ƒ(х)
зліва
при х → х ,
якщо вона є границею функції при х → х
,
якщо вона є границею функції при х → х по множині
по множині
 .
.
Визначення
7.
Нехай задана функція ƒ(х), х Х,
та х
Х,
та х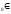 R.
Точка а називається границею
значень функції
ƒ(х)
справа
при х → х
R.
Точка а називається границею
значень функції
ƒ(х)
справа
при х → х ,
якщо вона є границею функції при х → х
,
якщо вона є границею функції при х → х по множині
по множині
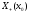 .
.
Однобічні
границі функції в точці позначаються
так:
 - границя функції зліва,
- границя функції зліва,
 - границя функції справа. Для позначення
границь в 0 та ±∞ використовують
позначення:
- границя функції справа. Для позначення
границь в 0 та ±∞ використовують
позначення:
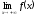 та
та
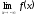 ;
;
 та
та .
.
Теорема.
Функція ƒ(х), х Х,
має границю в точці х
Х,
має границю в точці х =
sup
=
sup
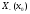 =
inf
=
inf ,
,
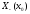 ≠Ø,
≠Ø,
 ≠Ø,
тоді та тільки тоді, коли в точці х
≠Ø,
тоді та тільки тоді, коли в точці х у функції ƒ(х) існують рівні границі
зліва та справа, причому загальне
значення цих границь є границею функції
ƒ(х) в точці х
у функції ƒ(х) існують рівні границі
зліва та справа, причому загальне
значення цих границь є границею функції
ƒ(х) в точці х .
.
Доведення.
Нехай
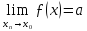 .
тоді за визначенням границі функції в
точці
.
тоді за визначенням границі функції в
точці
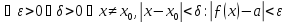 .
Для точок х таких, що
.
Для точок х таких, що
 та
та
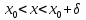 також справедлива рівність
також справедлива рівність
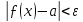 .
А це, відповідно до визначення по Коші,
означає, що число а є границею функції
ƒ як зліва, так і справа в точці
.
А це, відповідно до визначення по Коші,
означає, що число а є границею функції
ƒ як зліва, так і справа в точці
 ,
тобто
,
тобто
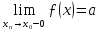 та
та
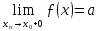 .
.
Нехай
виконано, що в точці х у функції ƒ(х) існують рівні границі
зліва та справа. Відповідно до визначення
границі функції зліва та справа в точці,
маємо, що
у функції ƒ(х) існують рівні границі
зліва та справа. Відповідно до визначення
границі функції зліва та справа в точці,
маємо, що
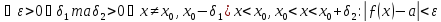 .
Якщо в якості
.
Якщо в якості
 обрати найменше з чисел
обрати найменше з чисел
 ,
то для всіх х, які задовольняють умові
х
,
то для всіх х, які задовольняють умові
х
 буде виконано
буде виконано
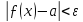 .
Цей означає, що
.
Цей означає, що
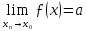 .
.
Визначення
8.
Функція ƒ(х), х Х,
називається неперервною зліва (справа)
в точці х
Х,
називається неперервною зліва (справа)
в точці х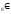 Х,
якщо
Х,
якщо
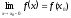 (
(
 ).
).
-
Нехай всі розглянуті функції визначені на множині Х
 R
та х
R
та х Х
– скінчена чи нескінченно віддалена
точка.
Х
– скінчена чи нескінченно віддалена
точка.
Властивості границі функції в точці.
-
Якщо функція ƒ(х) має в точці х
 скінчену границю, то існує така
окрестність точки х
скінчену границю, то існує така
окрестність точки х - U(х
- U(х ),
що функція ƒ(х) обмежена на перетині
Х∩U(х
),
що функція ƒ(х) обмежена на перетині
Х∩U(х ).
). -
Наслідки: Якщо функція ƒ(х) неперервна в точці х
 ,
то існує така окрестність точки х
,
то існує така окрестність точки х - U(х
- U(х ),
що функція ƒ(х) обмежена на перетині
Х∩U(х
),
що функція ƒ(х) обмежена на перетині
Х∩U(х ).
). -
Лемма про збереження знаку. Якщо функція ƒ(х) має в точці х
 скінчену границю відмінну від 0,тобто
скінчену границю відмінну від 0,тобто
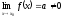 ,
то існує така окрестність точки х
,
то існує така окрестність точки х - U(х
- U(х )
та число с > 0, що для всіх точок
х
)
та число с > 0, що для всіх точок
х Х∩U(х
Х∩U(х )
виконана нерівність: ƒ(х) > с, якщо а
> 0; ƒ(х) < -с, якщо а < 0.
)
виконана нерівність: ƒ(х) > с, якщо а
> 0; ƒ(х) < -с, якщо а < 0.
-
Наслідки: Якщо функція ƒ(х) неперервна в точці х
 та ƒ(х
та ƒ(х )
≠ 0, то існує така окрестність точки
х
)
≠ 0, то існує така окрестність точки
х - U(х
- U(х )
та число с > 0, що для всіх точок
х
)
та число с > 0, що для всіх точок
х Х∩U(х
Х∩U(х )
виконана нерівність: ƒ(х) > с, якщо
ƒ(х
)
виконана нерівність: ƒ(х) > с, якщо
ƒ(х )
> 0; ƒ(х) < -с, якщо ƒ(х
)
> 0; ƒ(х) < -с, якщо ƒ(х )
< 0.
)
< 0.
-
Якщо функція ƒ(х) = с – стала, то
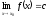 .
. -
Якщо функція ƒ(х) ≥ с та існує скінчена чи визначеного знаку нескінчена границя
 ,
то
,
то
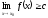 .
. -
Якщо φ(х) ≤ ƒ(х) ≤ ψ(х) та існують скінчені чи визначеного знаку нескінчені границі
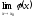 та
та
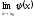 ,
вони рівні між собою, то
,
вони рівні між собою, то
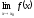 =
=
 =
=
 .
. -
Якщо існують скінчені границі
 та
та
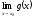 ,
то існують й скінчені границі
,
то існують й скінчені границі
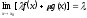
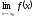 +
+

 ,
λ, μ
,
λ, μ
 R;
R;
 =
=
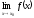
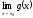 ,
та якщо
,
та якщо
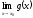 ≠ 0, то й
≠ 0, то й
 .
. -
Наслідки: Якщо функції ƒ(х) та g(х) – неперервні в точці х
 ,
то функції λƒ(х) + μg(х), λ, μ
,
то функції λƒ(х) + μg(х), λ, μ
 R,
ƒ(х)g(х) та ƒ(х)/g(х), де g(х
R,
ƒ(х)g(х) та ƒ(х)/g(х), де g(х )
≠ 0, неперервні в точці х
)
≠ 0, неперервні в точці х .
.
Доведення властивостей границі функції в точці провести самостійно. Можна скористатись підручником - Кудрявцев Л.Д. Курс математического анализа: Учебник. Для студентов университетов и вузов. В 3 т. - М.: Высшая школа,1998 – Том 1.
