
ман для 1ПМ-11 / 2 курс 2011 / лекции / Функції та їх границі / лекция № 9
.docxМіністерство освіти і науки, молоді та спорту України
Горлівський технікум Донецького національного університету
ЛЕКЦІЯ № 9
з теми: «Нескінченно малі та великі функції. Критерій Коші існування границі функції.»
Модуль КЗН-02. ПР.О.03.03 Функції та їх границі
Дисципліна: «Математичний аналіз»
Розглянуто та схвалено Розробив викладач
на засіданні циклової Велікодна О. В.
комісії інформаційних технологій
та прикладної математики.
протокол № 1 від 30.08.2011 р.
Голова циклової
комісії ІТ та ПМ І. П. Сошина
ПЛАН ЗАНЯТТЯ
Дата: курс: ІІ
Викладач: Велікодна Ольга Володимирівна.
Тема: Нескінченно малі та великі функції. Критерій Коші існування границі функції.
Мета:
-
Дидактична: вивчити основні властивості границі функції в точці, навчитись знаходити границі функції та застосовувати важливі границі.
-
Виховна: виховувати професійно зацікавлену особистість, здатну вільно мислити та логічно висловлювати свої думки.
-
Методична: вдосконалювати методику проведення лекції з використанням технологій проблемного та проектного навчання.
Тип: лекція № 9
Вид: лекція – дослідження проблемних питань.
Методи та форми проведення заняття: метод проблемного викладення матеріалу, репродуктивний, дослідницький.
Науково-методичне забезпечення:
-
Кудрявцев Л.Д. Курс математического анализа: Учебник. Для студентов университетов и вузов. В 3 т. - М.: Высшая школа,1998.
-
Кудрявцев Л.Д. Сборник задач по математическому анализу: Учебник для вузов. В 3 т. - М.: Наука. Гл. ред. физ. - мат. лит.,1989.
-
Берман Г.Н. Сборник задач по курсу математического анализа: Учеб. пособие для вузов. - М.: Наука. Гл. ред. физ. - мат. лит.,1975.
-
Марон А. И. Дифференциальное и интегральное исчисление в примерах и задачах. – М.: Наука, 1973.
Між предметні зв’язки:
-
Дисципліни, що забезпечують: елементарна математика
-
Дисципліни, що забезпечуються: лінійна алгебра та аналітична геометрія, дискретна математика, диференціальні рівняння, рівняння математичної фізики, чисельні методи, методи оптимізації, теорія функцій комплексної змінної.
Обладнання: зошити, ручки, крейда, дошка.
ХІД ЗАНЯТТЯ.
-
Організаційна частина:
-
відсутні;
-
підготовка до заняття;
-
перевірка д/з.
-
Актуалізація опорних знань:
-
Вивчення нового матеріалу:
-
Тема лекції: Нескінченно малі та великі функції. Критерій Коші існування границі функції.
-
Мотивація вивчення матеріалу: вивчити основне поняття математичного аналізу – границі функції в точці, яке дає можливість застосування апарату дослідження у будь – яких сферах прикладання математичних задач.
-
План вивчення нового матеріалу: надається в конспекті лекції.
-
Виклад нового матеріалу. Конспект лекції надається.
-
Закріплення нового матеріалу.
-
Підсумки заняття.
-
Домашнє завдання:
План лекції № 9.
-
Нескінченно малі та нескінченно великі функції, їх властивості та зв'язок.
-
Критерій Коші існування границі функції в точці.
Конспект лекції № 9.
Тема: «Нескінченно малі та великі функції. Критерій Коші існування границі функції.»
-
Визначення 1. Функція α(х), х
 Х,
називається нескінченно малою при х→
х
Х,
називається нескінченно малою при х→
х ,
якщо
,
якщо
 .
.
Нескінченно малі функції відіграють важливу роль в теорії границь функції в точці.
Лемма.
Для того, щоб у функції ƒ(х), х Х,
існувала в точці х
Х,
існувала в точці х скінчена границя а, необхідно та
достатньо, щоб функція α(х) = ƒ(х) – а була
нескінченно малою при х→ х
скінчена границя а, необхідно та
достатньо, щоб функція α(х) = ƒ(х) – а була
нескінченно малою при х→ х .
.
Дійсно,
якщо
 ,
то, визначаючи
,
то, визначаючи
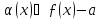 ,
отримаємо
,
отримаємо
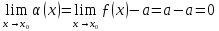 .
.
Зворотно,
якщо
 та
та
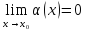 ,
то
,
то
 .
.
Властивості нескінченно малих.
-
Теорема. Лінійна комбінація скінченого числа нескінченно малих при х→ х
 функцій є нескінченно малою при х→ х
функцій є нескінченно малою при х→ х функцією.
функцією.
-
Добуток нескінченно малої при х→ х
 функції на обмежену функцію є нескінченно
малою при х→ х
функції на обмежену функцію є нескінченно
малою при х→ х функцією.
функцією. -
Наслідки: добуток скінченого числа нескінченно малих при х→ х
 функцій є нескінченно малою при х→ х
функцій є нескінченно малою при х→ х функцією.
функцією.
-
Теорема (критерій Коші): Для того, щоб функція ƒ(х), х
 Х,
мала в точці х
Х,
мала в точці х скінчену границю, необхідно та достатньо,
щоб для любого
скінчену границю, необхідно та достатньо,
щоб для любого
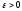 існувала такій проколотий окіл U(х
існувала такій проколотий окіл U(х )
точки х
)
точки х ,
щоб для будь – яких х′
,
щоб для будь – яких х′ Х∩U(х
Х∩U(х )
та х″
)
та х″ Х∩U(х
Х∩U(х )
виконувалась нерівність
)
виконувалась нерівність
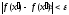 .
.
За допомогою символів критерій Коші записується таким чином:
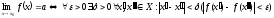 .
.
Доведення.
Доведення
необхідності.
Нехай
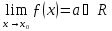 .
Це означає, що для будь-якого
.
Це означає, що для будь-якого
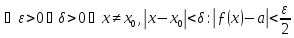 .
Нехай
.
Нехай
 ,
,
 ,
тоді
,
тоді
 .
.
Доведення
достатності.
Нехай функція
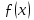 така, що
така, що
 та для всіх
та для всіх
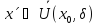 ,
,
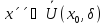 виконується нерівність
виконується нерівність
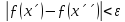 .
По-перше, з даної умови маємо, що функція
.
По-перше, з даної умови маємо, що функція
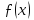 визначена
в деякім проколотому околі точки
визначена
в деякім проколотому околі точки
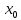 .
.
Перевіримо,
що існує границя функції в точці
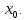 Візьмемо будь-яку послідовність
Візьмемо будь-яку послідовність
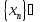
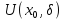 ,
,
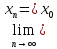 та довільно задамо
та довільно задамо
 .
.
Для
цього ε існує проколотий окіл
 ,
що задовольняє умовам
,
що задовольняє умовам
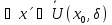 ,
,
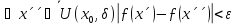 .
Далі, так як
.
Далі, так як
 ,
для околу точки
,
для околу точки
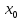 існує такий номер
існує такий номер
 послідовність
послідовність
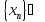
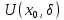 .
Але ж послідовність
.
Але ж послідовність
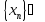
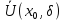 ,
тобто
,
тобто
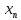
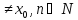 .
Звідси маємо, що
.
Звідси маємо, що
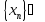
 ,
,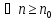 .
Тоді , для всіх
.
Тоді , для всіх
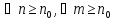 отримаємо
отримаємо
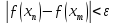 .
Тобто, послідовність
.
Тобто, послідовність
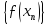 задовольняє критерію Коші для
послідовностей, й тому збігається.
задовольняє критерію Коші для
послідовностей, й тому збігається.
Таким
чином, для кожної послідовності

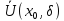 ,
,
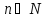 ,
яка задовольняє умові
,
яка задовольняє умові
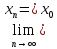 послідовність
послідовність
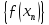 збігається. Звідси, на основі леми про
існування границі функції в точці, маємо
існування скінченої границі
збігається. Звідси, на основі леми про
існування границі функції в точці, маємо
існування скінченої границі
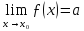 .
.
