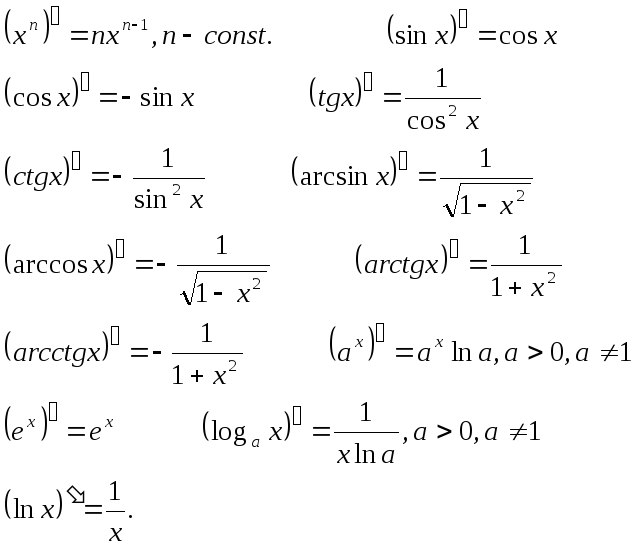ман для 1ПМ-11 / 2 курс 2011 / лекции / Похідна і диференціал / лекция № 15

Міністерство освіти і науки, молоді та спорту України

Горлівський технікум Донецького національного університету

ЛЕКЦІЯ № 15

з теми: «Визначення похідної, диференціала. Геометричний, фізичний зміст похідної,

диференціала. Правила обчислення похідних, пов'язані з арифметичними операціями.»

Модуль КЗН-02. ПР.О.03.05 Похідна і диференціал

Дисципліна: «Математичний аналіз»

Розглянуто та схвалено Розробив викладач

на засіданні циклової Велікодна О. В.

комісії інформаційних технологій

та прикладної математики.

протокол № 1 від 30.08.2011 р.

Голова циклової

комісії ІТ та ПМ І. П. Сошина

ПЛАН ЗАНЯТТЯ

Дата: курс: ІІ

Викладач: Велікодна Ольга Володимирівна.

Тема: Визначення похідної, диференціала. Геометричний, фізичний зміст похідної, диференціала. Правила обчислення похідних, пов'язані з арифметичними операціями.

Мета:

• Дидактична: вивчити основне поняття математичного аналізу – похідну, вивчити її властивості, навчитись диференціювати елементарні, складні та обернені функції.

• Виховна: виховувати професійно зацікавлену особистість, здатну логічно мислити та чітко формувати власні думки.

• Методична: вдосконалити методику проведення лекції з елементами проблемної та проектної технологій.

Тип: лекція № 15

Вид: лекція – дослідження.

Методи та форми проведення заняття: язикові, проблемно – пошукові, індуктивні.

Науково-методичне забезпечення:

1. Кудрявцев Л.Д. Курс математического анализа: Учебник. Для студентов университетов и вузов. В 3 т. - М.: Высшая школа,1998.

2. Кудрявцев Л.Д. Сборник задач по математическому анализу: Учебник для вузов. В 3 т. - М.: Наука. Гл. ред. физ. - мат. лит.,1989.

3. Берман Г.Н. Сборник задач по курсу математического анализа: Учеб. пособие для вузов. - М.: Наука. Гл. ред. физ. - мат. лит.,1975.

4. Марон А. И. Дифференциальное и интегральное исчисление в примерах и задачах. – М.: Наука, 1973.

Між предметні зв’язки:

• Дисципліни, що забезпечують: елементарна математика

• Дисципліни, що забезпечуються: лінійна алгебра та аналітична геометрія, дискретна математика, диференціальні рівняння, рівняння математичної фізики, чисельні методи, методи оптимізації, теорія функцій комплексної змінної.

Обладнання: зошити, ручки, крейда, дошка.

ХІД ЗАНЯТТЯ.

1. Організаційна частина:

1. відсутні;

2. підготовка до заняття;

3. перевірка д/з.

2. Актуалізація опорних знань.

3. Вивчення нового матеріалу:

• Тема лекції: Визначення похідної, диференціала. Геометричний, фізичний зміст похідної, диференціала. Правила обчислення похідних, пов'язані з арифметичними операціями.

• Мотивація вивчення матеріалу: вивчити основні поняття, пов’язані з диференціюванням елементарних функцій та їх застосуванням при розв’язанні прикладних задач.

• План вивчення нового матеріалу: надається в конспекті лекції.

4. Виклад нового матеріалу. Конспект лекції надається.

5. Закріплення нового матеріалу.

6. Підсумки заняття.

7. Домашнє завдання:

План лекції № 15.

1. Визначення похідної.

2. Диференціал функції.

3. Геометричний зміст похідної та диференціала.

4. Фізичний зміст похідної та диференціала.

5. Властивості похідних, пов'язані з арифметичними діями над функціями.

Конспект лекції № 15.

Тема: «Визначення похідної, диференціала. Геометричний, фізичний зміст похідної,

диференціала. Правила обчислення похідних, пов'язані з арифметичними операціями.»

1. Нехай функція у = ƒ(х) задана в околі Ů(х) точки хR, х Ů(х) та функція 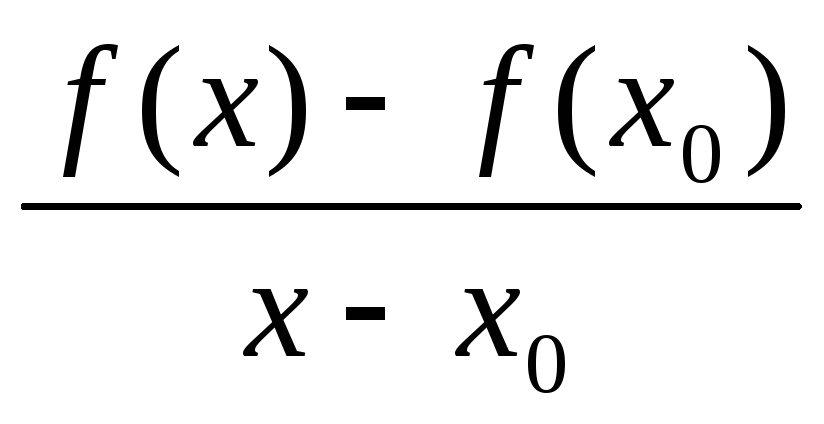визначена в проколотому околі Ů(х).

Визначення 1. Якщо існує границя , то вона називається похідною функції ƒ(х) в точці х та позначається . Тобто = .

Ця рівність означає, що похідна функції у = ƒ(х) в точці х дорівнює швидкості змінення змінної у відносно змінної х в вказаній точці. Якщо покласти та = , то = .

Операція обчислення похідної функції називається операцією диференцірування.

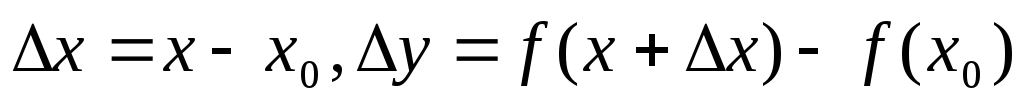2. Визначення 2. Функція у = ƒ(х) задана в околі Ů(х) точки хR, називається диференціруємою в точці х, якщо її приріст представимо у вигляді 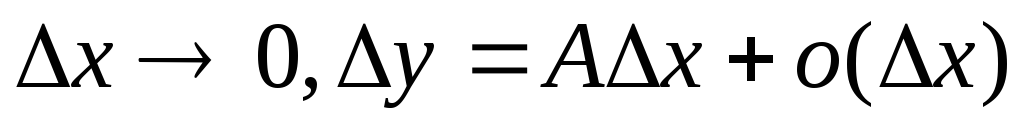, де А – стала. Лінійна функція AΔх називається диференціалом функції ƒ(х) в точці х та позначається d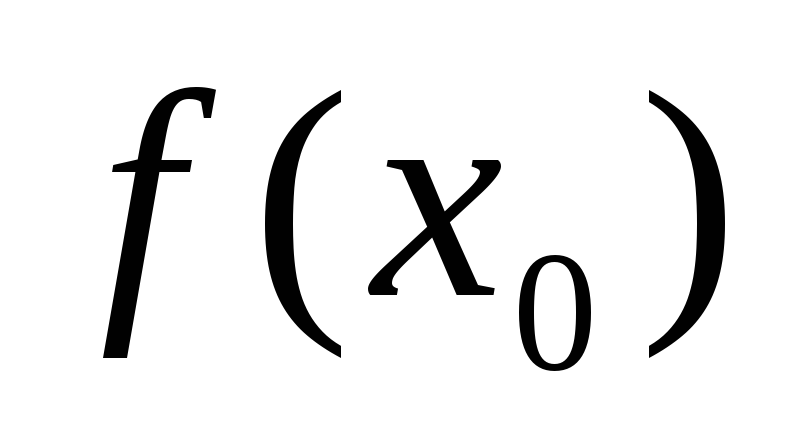 чи dy.

Маємо: . Позначаючи Δх = dх, отримаємо . Окрім того, .

Теорема. Функція є диференціруємою в деякій точці в тому та тільки в тому випадку, коли вона в цій точці має скінчену похідну.

Маємо: = , тобто =+. Тому . Це є умова диференцірування функції в точці х, причому = А.

Теорема. Якщо функція диференціруєма в деякій точці, то вона неперервна в цій точці.

3. Нехай функція у = ƒ(х) задана в околі Ů(х) точки хR, неперервна в цій точці, 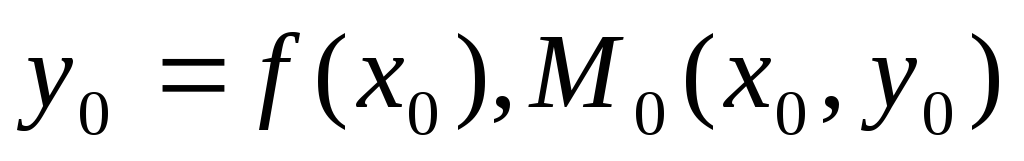. Зафіксуємо довільно приріст аргументу Δх, тільки щоб х+ Δх Ů(х). Тоді 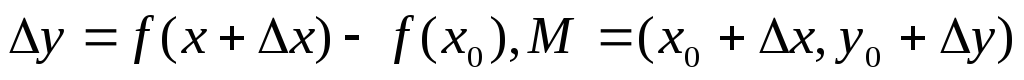. Рівняння прямої, що проходить крізь точки М0, М та називається січною графіка функції у = ƒ(х) має вид: у = 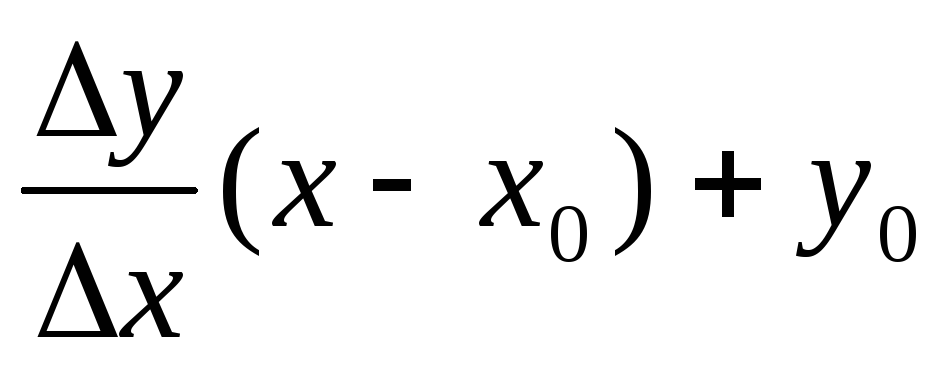. Граничне положення січної буде досягнено тоді та тільки тоді, коли буде існувати скінчена границя , тобто існувати скінчена похідна функції у = ƒ(х). Рівняння граничного положення січної, тобто дотичної до графіку функції у = ƒ(х) має вид: у = 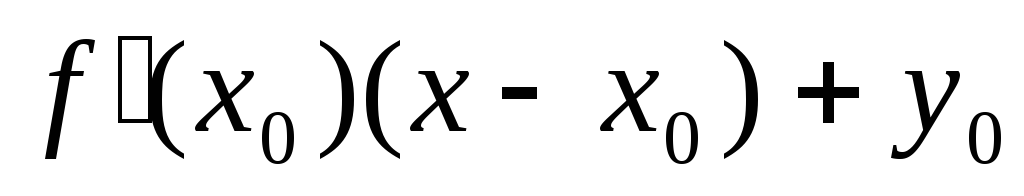, де 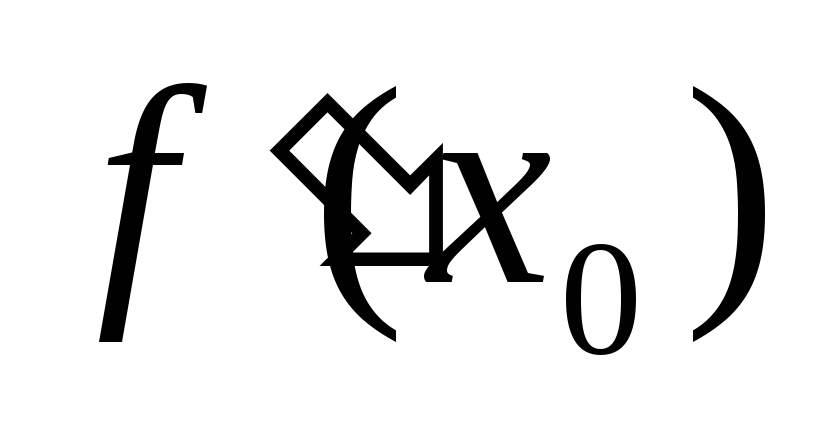= tgα, α – кут нахилу дотичної до осі ОХ – геометричний зміст похідної.

Якщо ординату точки дотику позначити у кас. та , то рівняння дотичної до графіку функції в точці має вид: . Маємо геометричний зміст диференціалу – диференціал функції дорівнює приросту ординати дотичної.

4. Нехай значення у та х – деякі фізичні величини, причому х змінюється в деякому проміжку, наприклад у відрізку [a, b]. Відношення 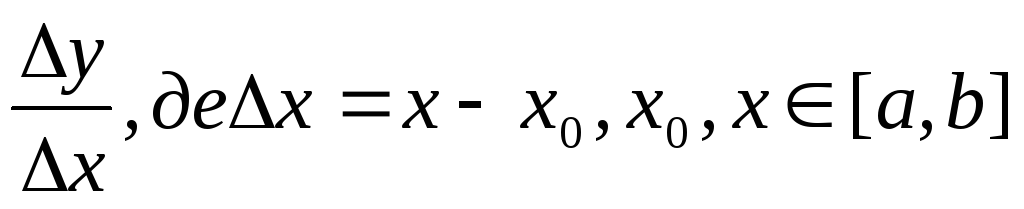, 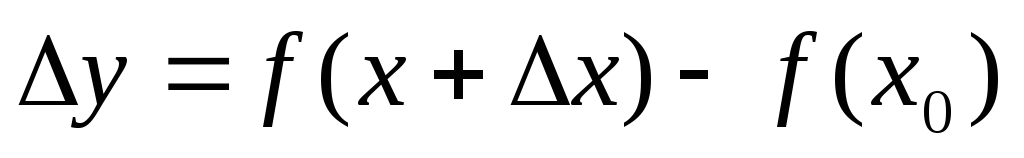називається середньою швидкістю змінення у відносно змінної х на відрізку [х0, х0+Δх].

Приріст лінійно залежить від Δх з точністю до нескінченно малої більш високого порядку. Це означає, що в малому фізичний процес, що описує функція ƒ(х), проходить практично лінійно.

• Якщо s = s(t) – довжина шляху, що проходить матеріальна точка за час t, то миттєва швидкість руху v = .

• Диференціал ds = vΔt дорівнює шляху, який пройшла б точка за проміжок часу Δt, починаючи з моменту часу t, якщо б рух на цьому відрізку шляху був рівномірним із швидкістю v. При цьому Δs = ds + о(Δt), Δt → 0.

• q = q(t) – кількість електрики, що пройшла крізь січення провідника в момент часу t, то сила току є I = .

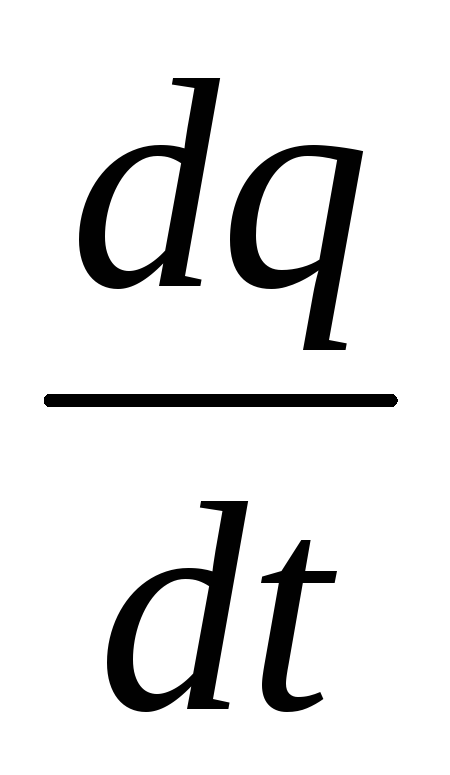• Диференціал dq = IΔt дорівнює кількості електрики, яка пройшла б крізь поперечне січення провідника за проміжок часу Δt, починаючи з моменту часу t, якщо б сила току була сталою та дорівнювала силі току в момент часу t. При цьому Δq = dq + о(Δt), Δt → 0.

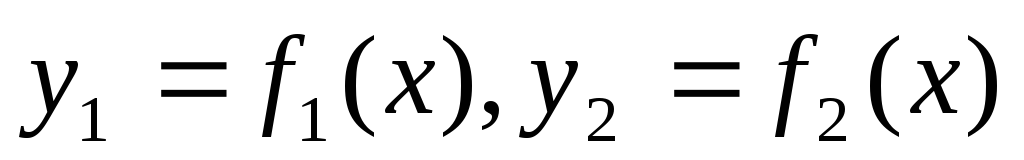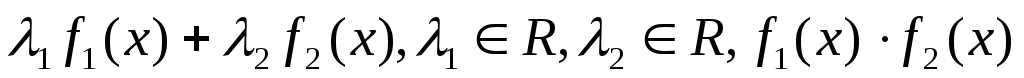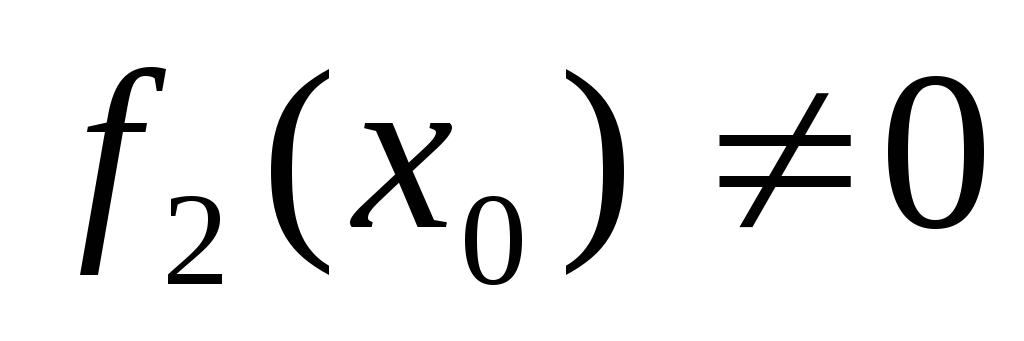5. Теорема. Якщо функції задані в околі точки хR, а в самій точці х мають скінчені похідні, то функції , а у випадку, коли і функції 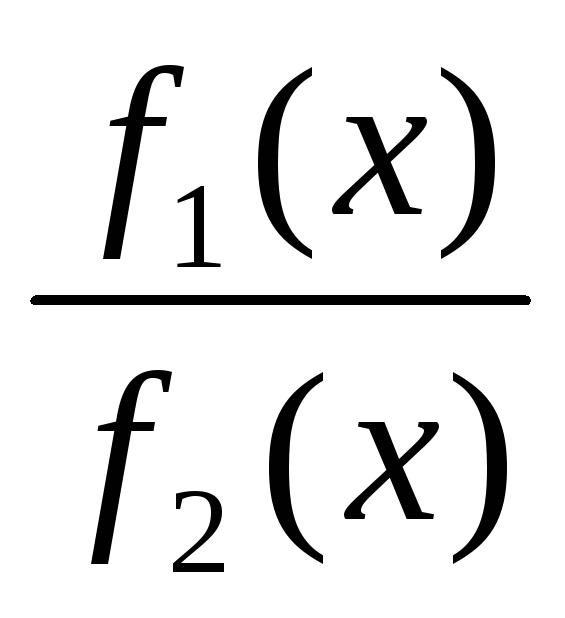також мають в точці х скінчені похідні. При цьому мають місце формули:

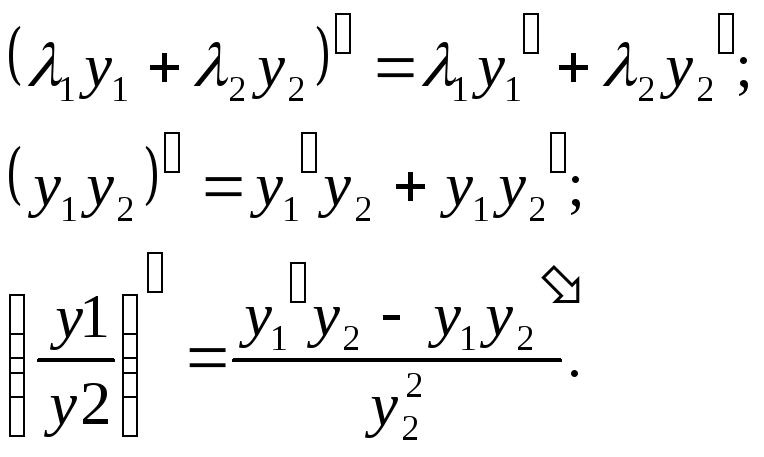
Таблиця похідних основних елементарних функцій.