ман для 1ПМ-11 / 2 курс 2011 / лекции / Похідна і диференціал / лекция № 17

Міністерство освіти і науки, молоді та спорту України

Горлівський технікум Донецького національного університету

ЛЕКЦІЯ № 17

з теми: «Теореми про середнє для диференційованих функцій.»

Модуль КЗН-02. ПР.О.03.05 Похідна і диференціал

Дисципліна: «Математичний аналіз»

Розглянуто та схвалено Розробив викладач

на засіданні циклової Велікодна О. В.

комісії інформаційних технологій

та прикладної математики.

протокол № 1 від 30.08.2011 р.

Голова циклової

комісії ІТ та ПМ І. П. Сошина

ПЛАН ЗАНЯТТЯ

Дата: курс: ІІ

Викладач: Велікодна Ольга Володимирівна.

Тема: Теореми про середнє для диференційованих функцій.

Мета:

• Дидактична: вивчити основні властивості елементарних функцій, пов’язаних із застосуванням похідної, навчитись застосовувати теореми про середнє при розв’язанні прикладних задач, навчитись диференціювати елементарні, складні та обернені функції.

• Виховна: виховувати професійно зацікавлену особистість, здатну логічно мислити та чітко формувати власні думки.

• Методична: вдосконалити методику проведення лекції з елементами проблемної та проектної технологій.

Тип: лекція № 17

Вид: лекція – дослідження.

Методи та форми проведення заняття: язикові, проблемно – пошукові, індуктивні.

Науково-методичне забезпечення:

1. Кудрявцев Л.Д. Курс математического анализа: Учебник. Для студентов университетов и вузов. В 3 т. - М.: Высшая школа,1998.

2. Кудрявцев Л.Д. Сборник задач по математическому анализу: Учебник для вузов. В 3 т. - М.: Наука. Гл. ред. физ. - мат. лит.,1989.

3. Берман Г.Н. Сборник задач по курсу математического анализа: Учеб. пособие для вузов. - М.: Наука. Гл. ред. физ. - мат. лит.,1975.

4. Марон А. И. Дифференциальное и интегральное исчисление в примерах и задачах. – М.: Наука, 1973.

Між предметні зв’язки:

• Дисципліни, що забезпечують: елементарна математика

• Дисципліни, що забезпечуються: лінійна алгебра та аналітична геометрія, дискретна математика, диференціальні рівняння, рівняння математичної фізики, чисельні методи, методи оптимізації, теорія функцій комплексної змінної.

Обладнання: зошити, ручки, крейда, дошка.

ХІД ЗАНЯТТЯ.

1. Організаційна частина:

1. відсутні;

2. підготовка до заняття;

3. перевірка д/з.

2. Актуалізація опорних знань.

3. Вивчення нового матеріалу:

• Тема лекції: Теореми про середнє для диференційованих функцій.

• Мотивація вивчення матеріалу: вивчити основні поняття, пов’язані з диференціюванням елементарних функцій та їх застосуванням при розв’язанні прикладних задач.

• План вивчення нового матеріалу: надається в конспекті лекції.

4. Виклад нового матеріалу. Конспект лекції надається.

5. Закріплення нового матеріалу.

6. Підсумки заняття.

7. Домашнє завдання:

План лекції № 17.

1. Теорема Ферма.

2. Теореми Ролля, Лагранжа та Коші про середні значення.

Конспект лекції № 17.

Тема: «Теореми про середнє для диференціруємих функцій.»

1. Визначення 1. Нехай функція ƒ(х) задана на множині Х та х Х. Якщо для всіх точок х Х виконується нерівність ƒ(х) ≤ ƒ(х) (ƒ(х) ≥ ƒ(х)), то говорять що функція ƒ(х) приймає в точці х найбільше (найменше) значення на множині Х.

Теорема.(Ферма) Якщо функція визначена в деякім околі точки х, приймає в цій точці найбільше (найменше) в розглянутім околі значення та має в точці х похідну, то ця похідна дорівнює 0.

Зауваження: точка х - внутрішня точка розглянутої множини.

Доведення. Нехай f(х) визначена в околі U(х₀) точки х₀ и приймає для визначеності при х=х₀ найбільше значення, тобто для всіх х з околу U(х₀) виконується нерівність f(х)≤ f(х₀). Тоді, якщо х<х₀, то а якщо х>х₀, то

Якщо існує похідна в широкому змісті, тобто, якщо існує скінчена або нескінчена, визначеного знаку, границя , то, переходячи до границі при х→х₀-0 та при х→х₀+0 отримаємо відповідно f ^´(х₀)≥0 та f ^´(х₀)≤0. Ці нерівності виконуються одночасно тільки при f ^´(х₀)=0.

Геометрична інтерпретація теореми Ферма складається з того, що якщо при х=х₀ функція f приймає найбільше чи найменше значення в деякому околі точки х₀, то дотична до графіку функції у відповідній точці паралельна до осі абсцис.

2. Теорема.(Ролля) Якщо функція ƒ(х)

   1. неперервна на відрізку [a, b];

   2. має в кожній точці інтервалу(a, b) скінчену чи визначеного знаку нескінчену похідну;

   3. приймає рівні значення на кінцях відрізку [a, b], тобто ƒ(а) = ƒ(b),

то існує хоча б одна така точка ξ [a, b], що ƒ′(ξ) = 0.

Доведення. Нам вже відомо, що функція, що неперервна на відрізку, приймає найбільше та найменше значення в деяких точках цього відрізку. Нехай М=mах f(х), m=mіn f(х) на відрізку [a; b]. Тоді, маємо m ≤ f(х) ≤ М для будь-якого х з відрізку [a; b].

Якщо m = М, то функція f(х) – стала та ƒ′(ξ) = 0 на відрізку [a; b] (у якості ξ можемо взяти будь-яку точку відрізку).

Якщо m ≠ М, то з умови f(а) = f(b) маємо, що хоча б одне зі значень m чи М не приймається на кінцях відрізку [a; b]. Нехай тим значенням буде М. Тоді на відрізку [a; b] існує точка ξ, така, що f(ξ) = М, тобто в цій точці функція приймає найбільше значення й на інтервалі (а, b). Тоді, користуючись теоремою Ферма, маємо ƒ′(ξ) = 0.

Геометрично теорема Ролля визначає, що на графіку неперервної на відрізку та диференційованої внутрі нього функції, що приймає на кінцях відрізку однакові значення, існує точка, в якій дотична паралельна до осі абсцис.

Зауваження. Всі вимоги теореми Ролля є суттєвими. (Привести приклади, що стверджують зауваження)

Теорему Ролля можна сформулювати наступним чином: між двома нулями диференційованої функції завжди лежить хоча б один нуль її похідної.

Теорема.(Лагранжа) Якщо функція ƒ(х)

1. неперервна на відрізку [a, b];

2. має в кожній точці інтервалу (a, b) скінчену чи визначеного знаку нескінчену похідну,

то існує хоча б одна така точка ξ (a, b), що ƒ(b) – ƒ(a) = ƒ′(ξ)(b – a).

Формула називається формулою скінчених приростів Лагранжа.

Доведення. Розглянемо допоміжну функцію F(х) = f(х) – λх та визначимо число λ таким чином, щоб F(а) = F(b), тобто щоб f(а) – λа= f(b) – λb. Це означає, що λ =.

Для функції F виконуються всі умови теореми Ролля. Тому, існує хоча б одна точка ξ, така, що а<ξ<b, що . Тоді, .

Геометричний зміст теореми Лагранжа в тому, що на дузі АВ графіку функції з кінцями у точках А = (а, ƒ(a)), В = (b, ƒ(b)) знайдеться точка М = (ξ, ƒ(ξ)), дотична в якій паралельна хорді АВ.

, де - тангенс кута нахилу хорди АВ, - тангенс кута нахилу дотичної до дузі АВ в точці М = (ξ, ƒ(ξ)).

Наслідки. Якщо функція ƒ(х) неперервна на відрізку та у всіх його внутрішніх точках має похідну, що дорівнює 0, то функція стала на вказаному проміжку

Наслідки. Якщо функція ƒ(х) неперервна на деякім проміжку(скінченім чи нескінченім) та у всіх його внутрішніх точках має похідну, що дорівнює 0, окрім, можливо, скінченого числа його точок, то функція ƒ(х) стала на вказаному проміжку.

Наслідки. Якщо функція ƒ(х) неперервна в околі U(х) точки х, диференційована в проколотому околі Ů(х) та існують скінчена чи нескінчена границя , то існує скінчена чи нескінчена похідна .

Теорема.(Коші) Якщо функції ƒ та g

1. неперервні на відрізку [a, b];

2. диференційовані в кожній точці інтервалу (a, b);

3. g′(х) ≠ 0 у всіх точках х(a, b),

то існує така точка ξ (a, b), що .

Доведення. Розглянемо допоміжну функцію F(х) = f(х) – λg(х), де число λ оберемо таким чином, що F(а) = F(b), тобто f(а) – λg(а)= f(b) – λg(b). Тоді, λ=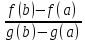. Функція F задовольняє всім умовам теореми Ролля. Тому, існує хоча б одна точка ξ, така, що а<ξ<b, що . Тобто, 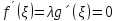та, відповідно, λ = = . Отриману формулу називають формулою скінчених приростів Коші.