-
Чому дорівнює ?
а) ∞;
б) 0;
в) не існує;
г) 3/5; •
-
Скільки раціональних чисел існує між числами 1 і 2?
а) жодного;
б) 1;
в) 3;
г) нескінченно багато; •
-
Не є елементарною функція
а) sign(x); •
б) е
;
в) х ²;
г) arcsin х;
-
Знайти
.
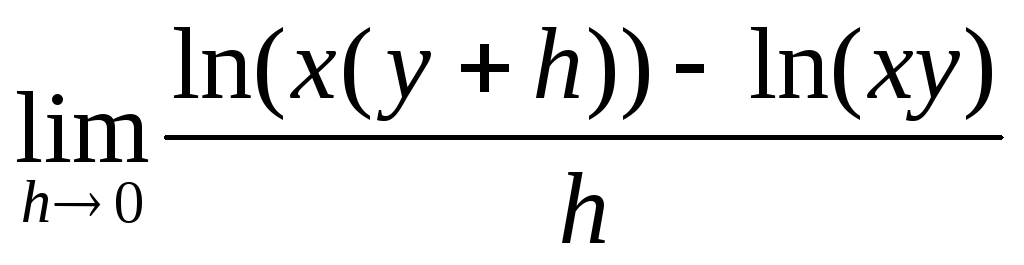а)
;
б)
;
в)
;
г)
;
•
-
Яка функція не є парною?
а) arcsin х + cos х; •
б) sin x ∙ tg x;
в) cos x + 1;
г) х ² - cos x;
-
Послідовність доданків
.
Тоді:
а)
розбігається;
б)
може розбігатися; •
в)
розбігається;
г)
збігається;
-
При х → ∞ , х + sin х ~ f(х), якщо f(х) = :
а) х ²;
б) х; •
в)
;
г) е
;
-
Ряд
збігається,
ряд
розбігається. Що вірно? (
)
а)
може
як збігатись, так і розбігатись;
б)
розбігається; •
в)
збігається;
г)
збігається;
-
Функція неперервна на відрізку і на його кінцях приймає значення різних знаків. Тоді на цьому відрізку функція
а) монотонна;
б) обертається в нуль; •
в) знакостала;
г) не обертається в нуль;
-
Послідовність {xn} називається фундаментальною, якщо
а)
;
б)
;
•
в)
;
г)
;
-
Ряд
збігається
при:
а)
;
б)
;
в)
;
•
г)
;
-
У функцій f та g : [a; b] → R
рівні похідні. Тоді
а) f і g розрізняються на лінійну функцію 2х + 1;
б) f і g співпадають;
в) їх сума – функція розривна;
г) f і g відрізняються на константу; •
-
Яка з функцій має лінію точок розриву?
а)
;
б)
;
•
в)
;
г)
;
-
Функція
має такі вертикальні асимптоти:
а) х = 1; •
б) х = 2;
в) х = 0 та х = 1;
г) х = 0;
-
Чому дорівнює ?
а) e ²;
б) e; •
в)
;
г)
;
-
Чому дорівнює множина значень функції у = arctg
?
а) 0 ≤ у < π/2;
б) 0 ≤ у < π/4;
в) –π/2 < у < π/2;
г) – π/4 ≤ у ≤ π/4; •
-
Знайти рівняння дотичної до графіка функції у = 0,5х ² - 0,5х + 1 в точці х0 = 8.
а) 7,5х + 80;
б) інша відповідь;
в) 7,5х – 31; •
г) 7,5х;
-
Знайти значення похідної в точці : f(х) = sin х + cos х, х0 = 0.
а) 1; •
б) – 1;
в) інша відповідь;
г) 0;
-
f1(х) неперервна на [ - 1, 0], а f2(х) неперервна на [0, 1]. Тоді функція у =
:
а) розривна в точці х = 0;
б) у(х) неперервна в точці х = 0, якщо f1(0) = f2(0); •
в) в точці х = 0 функція диференційована;
г) неперервна в точці х = 0;
-
Знайти найменше значення функції f(х) = х² + 2х – 5.
а) -6; •
б) 3;
в) -5;
г) -2;
-
Функція визначена на відрізку і монотонно зростає. Тоді
а) функція необмежена;
б) функція обмежена; •
в) функція неперервна;
г) вона має похідну;
-
Нехай f(х) задана на проміжку (a; b). Яке твердження правильне?
а) якщо f(х) не має нулів в (a; b), то вона знакопостійна в ньому;
б) якщо f(х) неперервна в (a; b), то вона обмежена в ньому;
в) якщо
f(х) неперервна в (a; b) і
(a; b), де f(х0)
= 0, то знайдуться такі х1
та х2,
що f(х1)
· f(х2)
< 0;
г) якщо f(х) неперервна в (a; b) і не має нулів в (a; b), то вона знакопостійна; •
-
Дано ступеневий ряд
.
Його область збіжності може бути:
а)
;
б)
;
в)
;
•
г)
;
-
Яка з функцій не має жодного локального екстремуму?
а)
;
б)
;
в)
;
г)
;
•
-
Обчислити інтеграл
.
а) 0; •
б) 1;
в) інша відповідь;
г) ½;
-
Знайти похідну функції
.
а)
;
•
б)
;
в)
;
г)
;
-
Ряд
збігається до
в (а; b). Яке з тверджень вірне?
а)
;
•
б)
неперервна
в (а; b);
в) ряд
збігається рівномірно до
;
г)
інтегрована
в (а; b);
-
Нехай S(t) площа області, обмеженої осями координат, графіком від'ємно означеної функції f(х) та прямої х = t, t > 0. Чому дорівнює
?
а) – f ′ (t);
б) – f(t); •
в) f(t);
г)
?
-
Якщо існує
,
то :
а) f визначена в точці х0;
б) f неперервна в точці х0;
в) f має розрив в точці х0;
г) f обмежена в деякому проколотому околі точки х0; •
-
xn → a > 0 коли n → ∞. Яке з тверджень невірне?
а)
;
б)
;
•
в)
;
г)
;
-
Нехай f(х) → 0 при х → a. Тоді:
а) sin f(х) ~ ln f(х) при х → a;
б) sin f(х) ~ tg f(х) при х → a; •
в) sin
f(х) ~ e
при х → a;
г) sin f(х) ~ cos f(х) при х → a;
-
Функція строго зростає на інтервалі. Тоді на цьому інтервалі функція
а) неперервна;
б) має обернену, яка строго зростає; •
в) має обернену, яка строго спадає;
г) диференційована;
-
Яка з рівностей вірна?
а)
;
б)
;
в)
;
•
г)
;
-
Нехай
та
- дві підпослідовності послідовності
.
Яке твердження правильне?
а) якщо
,
то
і
;
•
б) якщо
і
,
то
;
в) якщо
розбігається, то
та
- необмежені;
г) якщо
обмежена, то
збіжна;
-
Швидкість тіла, що рухається прямолінійно, визначається за законом v(t) = 3t + t² (t – в секундах, v – в м/с). Знайти прискорення тіла через 4 секунди після початку руху.
а) інша відповідь;
б) 35 м/с²;
в) 11 м/с²; •
г) 6 м/с²;
-
дорівнює:
а) ∞;
б) – 1;
в) 0;
г) 1; •
-
Функція
необмежена і неперервна. На якій з
областей вона визначена?
а)
;
б)
;
в)
;
г)
;
•
-
Тейлорово розвинення функції
в околі
має вигляд
.
Яке з тверджень вірне?
а) точка
- критична;
б)
монотонно зростає в околі
;
в)
- точка перегину;
г)
монотонно спадає в околі
;
•
-
Функція у = ln|х| має похідну тільки в таких точках:
а)
;
б)
;
в)
;
г)
;
•
-
Функція
неперервна. Тоді
а) f – диференційована;
б) f – непарна;
в) f – інтегрована; •
г) f ² - розривна;
-
Довільна фундаментальна послідовність
а) нескінченно велика;
б) нескінченно мала;
в) монотонна;
г) обмежена; •
-
Нехай
.
Яке твердження правильне?
а) f(х) не є неперервною в х0;
б) f(х) диференційована в х0;
в) f(х) має границю в х0; •
г) f(х) неперервна в х0;
-
Визначити кількість точок х0, в яких границя
не
існує.
а) 2;
б) 4;
в) 1; •
г) 0;
-
Знайти похідну функції у = cos(2 – 3х).
а) 3sin(2-3х); •
б) sin(2-3х);
в) 2sin(2-3х);
г) інша відповідь;
-
Яке твердження еквівалентно умові
?
а)
;
б)
;
в)
послідовність
є нескінченно малою; •
г)
;
-
Область визначення функції
є:
а) х > 0; •
б) х ≤ 0;
в) х ≥ 0;
г) х < 0;
-
Якщо послідовність
збігається, то вона:
а) обмежена; •
б) зростаюча;
в) нескінченно мала;
г) монотонна та обмежена;
-
Обчислити інтеграл
.
а) інша відповідь;
б) ¾; •
в) ¼;
г) 2/3;
-
Нехай
.
Тоді послідовність
а) є збіжною при а = 0;
б) може бути збіжною тільки при а = 0; •
в) завжди є розбіжною;
г) може бути збіжною також при а ≠ 0;
-
Достатня умова збіжності ряду:
а)
;
•
б)
;
в)
;
г)
;
-
Яким числом треба довизначити функцію
в точці х = 0, щоб вона була неперервною?
а) ln2; •
б) 2;
в) 1/ln2;
г) 1;
-
Функція неперервна на відрізку і на його кінцях приймає значення різних знаків. Тоді на цьому відрізку функція
а) диференційована;
б) монотонна;
в) обертається в нуль; •
г) не обертається в нуль;
-
Функція
неперервна на компактній множині
.
Яке твердження правильне?
а)
;
б) графік
функції
в
кожній точці
має дотичну площину;
в)
диференційована
у внутрішніх точках Е
г)
обмежена
на Е; •
-
Множина А є обмеженою тоді, та лише тоді, коли
а)
;
•
б)
;
в)
;
г)
;
-
Знайти тангенс кута нахилу дотичної до графіка функції
в точці х0
= 0.
а) інша відповідь;
б) 2; •
в) 1;
г) -1;