216. Чому дорівнює ?

а) ¾;

б) 0;

в) ∞;

г) 4/3; •

217. Скільки ірраціональних чисел існує між числами 2,5 і 3,5?

а) нескінченно багато; •

б) 4;

в) 1;

г) жодного;

218. Функція f(х) неперервна, а приріст аргументу ∆х → 0. Яка з властивостей приросту ∆f справедлива завжди?

а) ∆f < 0;

б) ∆f > 0;

в) ∆f = 0;

г) ∆f → 0; •

219. Яке твердження є вірним?

а) добуток двох непарних функцій є непарна функція;

б) сума парної і непарної функцій є непарна функція;

в) добуток парної і непарної функцій є непарна функція; •

г) жодна з вказаних вище;

220. Функція неперервна на відрізку. Тоді на цьому відрізку функція

а) приймає своє найбільше значення; •

б) диференційована;

в) не обмежена;

г) опукла;

221. А = В тоді і тільки, коли

а) ;

б) та ; •

в) серед відповідей 1 – 3 вірної немає;

г) ;

222. Знайти для f(х) = 4х³ + 2х – 3х² - 1 первісну, графік якої проходить через точку А(1; -1).

а) ;

б) інша відповідь;

в) ; •

г) ;

223. Чому дорівнює ?

а) інша відповідь;

б) 0;

в) не існує; •

г) ∞;

224. Для виконуються такі твердження:

а) збігається абсолютно;

б) збігається; •

в) ;

г) розбігається;

225. Ряд 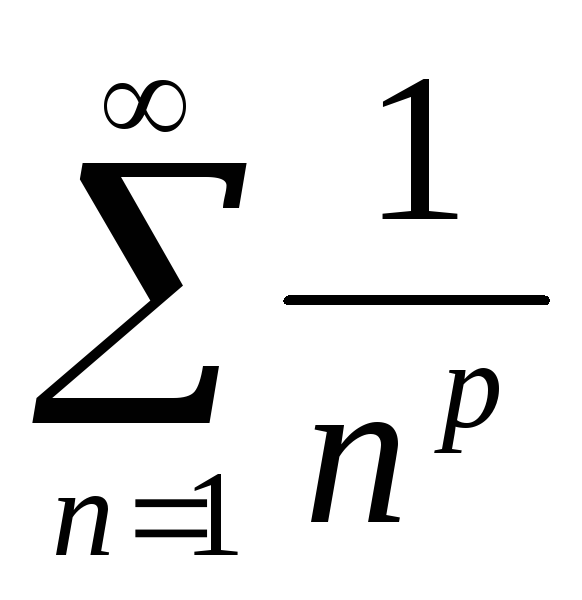збігається при:

а) завжди розбігається;

б) р > 0;

в) р < 1;

г) р > 1; •

226. Нехай {Xn} – збіжна. Тоді {СXn} – збіжна:

а) тільки при С = 1;

б)тільки при С = 0;

в) для довільного С; •

г) ніколи (таких С не існує);

227. Обчислити площу фігури, що обмежена лініями .

а) інша відповідь;

б) 1;

в) 1,5;

г) 2; •

228. Яка з формул не є вірною в загальному випадку?

а) жодна з вказаних вище;

б);

в) ;

г) ; •

229. При ∆х → 0, ∆f(х) теж збігається до 0. Це значить, що

а) f(х) непарна;

б) f(х) монотонно зростає;

в) f(х) неперервна; •

г) f(х) диференційована;

230. Чому дорівнює logх?

а) – 6/5;

б) 6/5;

в) - 3/10; •

г) 3/10;

231. дорівнює

а) ; •

б) ;

в) ;

г) ;

232. f(х) і g(х) розривні на (a; b). Яке з тверджень завжди вірне?

а) h(х) = f(х) + g(х) не означена в точці х0, якщо f(х) не означена в точці х0; •

б) h(х) = f(х) · g(х) розривна на (a; b);

в) h(х) = f(х) + g(х) означена на (a; b);

г) h(х) = f(х) + g(х) розривна на (a; b);

233. Нехай - нескінченно мала послідовність (), - збіжна послідовність. Яке твердження правильне?

а) - розбігається;

б) - збігається; •

в) - збігається;

г) - збігається;

234. Яка з функцій не є монотонною на області визначення?

а) |x| + х;

б) ;

в) ; •

г) ;

235. Похідна n – го порядку функції у = ln x має вигляд

а) ; •

б) ;

в) ;

г) ;

236. У множині Е = (-1; 4) максимальний елемент дорівнює

а) 4;

б) 3,9;

в) 3;

г) не існує; •

237. Якщо послідовність обмежена, то

а) вона монотонна;

б) будь – яка її підпослідовність збігається;

в) вона збігається;

г) вона має підпослідовність, яка збігається; •

238. Обчислити інтеграл ;

а) 0; •

б) 1;

в) інша відповідь;

г) -1;

239. Чому дорівнює ?

а) π/2;

б) ∞; •

в) 0;

г) 1;

240. Ряд збігається за ознакою

а) інтегральною;

б) Лейбніца; •

в) Даламбера;

г) Коші;

241. Яка з перерахованих властивостей функції у = 2sin х є вірною?

а) зростає на R;

б) неперіодична;

в) непарна; •

г) парна;

242. , то в точці х0 функція f(х)

а) може мати розрив першого роду; •

б) може мати розрив другого роду;

в) розривна;

г) неперервна;

243. Нехай ряд - збігається, а ряд - розбігається. Яке твердження правильне?

а) - збігається;

б) - збігається;

в) - розбігається;

г) - розбігається; •

244. Яка з плоских множин є замкненою?

а) ;

б) ; •

в) жодна з плоских множин не є замкненою;

г) ;

245. Знайти область визначення функції .

а) ;

б) ;

в) ; •

г) інша відповідь;

246. Матеріальна точка рухається прямолінійно за законом S(t) = 2 + 20t - 5t² (t – в секундах, S – в метрах). Знайти миттєву швидкість в момент часу t=5с.

а) 30 м/с;

б) інша відповідь;

в) 10 м/с; •

г) 12 м/с;

247. Визначити кількість точок х0, в яких границя не існує.

а) 4;

б) 1; •

в) 0;

г) 2;

248. дорівнює

а) не існує;

б) 5; •

в) 1;

г) 0;

249. Одна з частин формули бінома Ньютона може мати вигляд:

а) ;

б) ;

в) ; •

г) ;

250. Пряма у = 2х – 2 є асимптотою графіка функції при х → ∞

а) ;

б) ;

в) ; •

г) ;

251. Нехай Xn – збігається, а послідовність Yn – розбігається. Тоді їх сума Xn + Yn є послідовність, яка:

а) фундаментальна;

б) розбігається; •

в) може як збігатись, так і розбігатись;

г) збігається;

252. Нехай . Чому дорівнює ?

а) 5!+4!+3!;

б) 4!; •

в) 5!+4!;

г) 4!+3!;

253. Якщо послідовність збігається, то

а) вона має необмежену підпослідовність;

б) вона має монотонну підпослідовність; •

в) вона необмежена;

г) будь – яка її підпослідовність монотонна;

254. Функція монотонна на відрізку. Тоді на цьому відрізку функція

а) не обмежена;

б) неперервна;

в) інтегрована за Ріманом; •

г) диференційована;

255. Асоціативність додавання означає, що для довільних a, b, c

а) a + (b + c) = (a +b) + c; •

б) (ab) + c = (a + c)(b + c);

в) a + b = b + a;

г) (a + b)c = aс + bc;

256. Нехай існує скінчена границя . Яке твердження правильне?

а) існує окіл, в якому f(х) обмежена; •

б) f(х) обмежена в проміжку ;

в) f(х) неперервна в будь – якому [c; d] ;

г) f(х) неперервна в проміжку ;

257. Нехай функція f(х) є неперервною на проміжку (a; b). Тоді для довільних c, d: a ≤ c < d ≤ b на (c; d) функція f(х)

а) є рівномірно неперервною;

б) є диференційованою;

в) обов'язково є обмеженою;

г) може бути необмеженою; •

258. Яке з вказаних чисел є раціональним?

а) π;

б) ;

в) ; •

г) ℮;

259. Необхідна умова збіжності ряду:

а) ;

б) ;

в) ;

г) ; •

260. Яка найбільша кількість елементів може бути в скінченій множині?

а) скільки зірок на небі;

б) скільки елементарних частинок у всесвіті;

в) правильної відповіді не існує; •

г) залежить від природи елементів з яких складається множина;

261. Нехай . Тоді :

а) для довільного c;

б) ніколи ( таких с не існує);

в) якщо с = 0;

г) якщо с = 1; •

262. Чому дорівнює область визначення функції у = loglog х ? а) 0 < х < ½;

б) 0 < х < 1; •

в) ½ < х < 1;

г) 1 < х < +∞;

263. Точками розриву функції у = 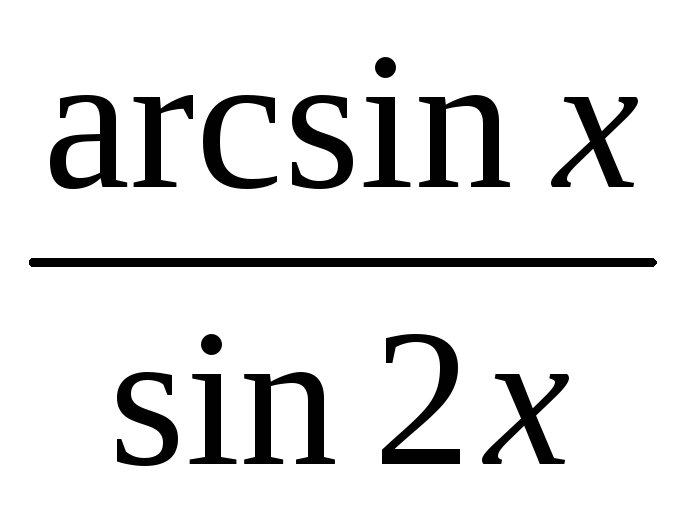є

а) ;

б) х = 0; •

в) х = 0, ± π;

г) ;

264. В інтервалі збіжності ступеневого ряду даний ряд:

а) збігається умовно в кожній точці;

б) збігається абсолютно в кожній точці; •

в) розбігається у кожній точці;

г) у деяких точках збігається, у деяких розбігається;

265. Який з інтегралів дорівнює нулеві?

а) ; •

б) ;

в) ;

г) ;

266. ∫ sin2xdx дорівнює

а) – cos2х + С;

б) – (1/2)cos2х + С; •

в) 2cos2х + С;

г) cos2х + С;

267. Для виконуються такі твердження:

а) розбігається для х = 1;

б) розбігається ;

в) збігається рівномірно на ; •

г) збігається нерівномірно на ;

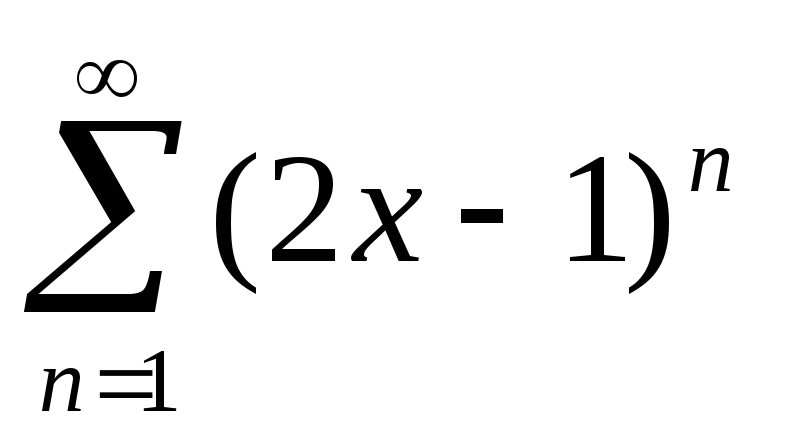268. Ряд збігається при:

а) ;

б) ;

в) ;

г) ; •

269. Скільки граничних точок має послідовність {cos } ?

а) 3;

б) 8;

в) 5; •

г) 2;