-
Чому дорівнює ?
а) 1;
б) не існує; •
в) 0;
г) ∞;
-
Який з наступних рядів збіжний?
а)
;
б)
;
•
в)
;
г)
;
-
Послідовність {Xn} називається нескінченно малою, якщо
а) вона розбігається;
б) вона збігається;
в) її границя дорівнює певного знака нескінченності;
г)
;
•
-
Нехай f(х) неперервна в х0, g(х) – розривна в х0. Яке твердження правильне?
а) f(х)·g(х) – розривна в х0;
б) f(х) + g(х) – розривна в х0; •
в) f(х)·g(х) – неперервна в х0;
г) g²(х) - розривна в х0;
-
Яка з плоских множин є відкритою?
а)
;
•
б)
;
в)
;
г) жодна з плоских множин не є замкненою;
-
Чому дорівнює ?
а) не існує;
б) e; •
в) 1;
г) ∞;
-
Ряд
збігається при:
а)
;
б) лише при х = 1; •
в) всіх х;
г)
;
-
Нехай Х – універсальна множина.
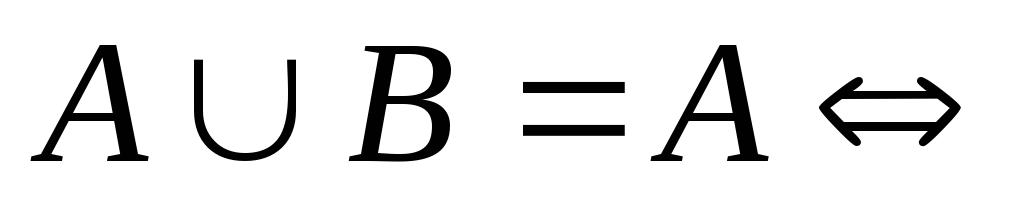
а)
;
•
б)
;
в) A = X;
г)
;
-
Чи може необмежена на множині
функція
бути неперервною на
,
якщо:
а)
;
б)
;
в)
;
г)
;
•
-
Нехай
.
Тоді (0, 0) є точкою:
а) мінімуму; •
б) розриву для цієї функції;
в) глобального максимуму;
г) локального мінімуму;
-
Область визначення функції
:
а)
;
б)
;
в)
;
г)
;
•
-
Функція кожне своє значення приймає лише один раз. Тоді вона
а) має обернену функцію; •
б) неперервна;
в) обмежена;
г) диференційована;
-
Різниця двох рядів, що збігаються, є ряд який:
а) збігається; •
б) може як збігатись, так і розбігатись;
в) розбігається;
г) умовно збігається;
-
Функція
неперервна на множині
.
Яке твердження правильне?
а) графік
функції
в
кожній точці
має дотичну площину;
б)
;
в)
диференційована
у внутрішніх точках Е
г)
обмежена
на Е; •
-
дорівнює
а) ∞;
б) не існує;
в) 1;
г) 0; •
-
Нехай f(х) визначена в проміжку Х і множина її значень – проміжок Y. Яке твердження правильне?
а) якщо
f(х) строго монотонна в Х, то в Y існує
обернена функція f
(у);
•
б) якщо
f(х) не є строго монотонною в Х, то f
(у)
не існує;
в) якщо
в Y існує обернена функція f
(у),
то f(х) є строго монотонною в Х;
г) якщо
f(х) неперервна в Х, то в Y існує обернена
функція f
(у);
-
Дана множина точок у яких перша координата раціональна, друга - ірраціональна. Що є межею цієї множини?
а) множина точок, у якої перша координата ірраціональна, друга – раціональна;
б) не можливо встановити;
в) множина точок, у якої обидві координати раціональні;
г) вся площина; •
-
Який з десяткових дробів є періодичним?
а) 0,1234…9101112…;
б) 0,112123124…;
в) 0,123456456…; •
г) 0,010010001;
-
Функція
зростає на інтервалі
а) (- ∞; 6); •
б) (0; + ∞);
в) (6; +∞);
г) (0; 6);
-
.
Яке твердження правильне?
а)
;
б)
;
•
в)
;
г)
;
-
У точці локального екстремуму:
а) похідна, якщо існує, дорівнює нулю; •
б)функція неперервна;
в)функція не визначена;
г)функція диференційована;
-
Нехай функція f(х) є неперервною на проміжку (a; b). Тоді на (a; b) функція f(х):
а) обов'язково є обмеженою;
б) може бути необмеженою; •
в) в деяких точках може мати стрибки;
г) є рівномірно неперервною;
-
Нехай функція f(х) неперервна на [а, b]. Яке твердження правильне?
а) f(х) - обмежена на [a;b]; •
б) f(х) - диференційована на (a;b);
в) якщо існує х0 : f(х0) = 0, то f(a)·f(b) < 0;
г) в будь – якій точці х0 з (a; b) існує дотична до графіка у = f(х) у точці (х0, f(х0));
-
Знайти загальний вигляд первісних для
.
а)
;
•
б)
;
в)
;
г) інша відповідь;
-
Яка з плоских множин є і не відкритою і не замкненою?
а) жодна з плоских множин не відповідає цим умовам;
б) y <x <2y;
в) x ≤y ≤x² +1;
г) x ≤y <x² +1; •