ПИТАННЯ ПІДСУМКОВОГО ТЕСТУВАННЯ З ДИСЦИПЛІНИ «МАТЕМАТИЧНИЙ АНАЛІЗ» ДЛЯ СТУДЕНТІВ 4 КУРСУ СПЕЦІАЛЬНОСТІ «ПРИКЛАДНА МАТЕМАТИКА»

1. Матеріальна точка рухається за законом S(t)=t³-4t² (t – в секундах, S – в метрах). Знайти швидкість в момент часу t=5с.

а) 115 м/с;

б) 35 м/с; •

в) інша відповідь;

г) 20 м/с;

2. Похідна функції у = cos(x²) дорівнює

а) –sin(x²);

б) 2хsin(x²);

в) -2хsin(x²); •

г) sin(x²);

3. >0, де . Яке твердження вірне?

а) f(х)>0 при будь-якому х[a;b];

б) f(х) – неперервна в [a;b];

в) f(х) – диференційована в [a;b];

г) f(х) – обмежена на [a;b]; •

4. Степеневі ряди та збігаються при х = 5. Знайти найбільший проміжок де обидва ряди повинні збігатись.

а) -1<x<5; •

б) -5<x<5;

в) -3<x<5;

г) -1<x<6;

5. Дана множина точок, у яких перша координата раціональна, а друга – ірраціональна. Що є межею цієї множини?

а) вся площина; •

б) множина точок, у якої перша координата ірраціональна, а друга раціональна;

в)множина точок, у якої обидві координати раціональні;

г)не можливо встановити;

6. Ряд збігається за ознакою

а) інтегральною; •

б) Даламбера;

в) Лейбніца;

г) Коші;

7. В множині Е=(10; 15,9] максимальний елемент дорівнює

а) не існує;

б) 15,9; •

в) 15;

г) 10;

8. Знайти точки екстремуму функції у = х³ - 6х².

а) ; •

б) ;

в) ;

г) інша відповідь;

9. Відомо, що похідна функції у =f(х) на проміжку [0;5] дорівнює (3х+2). Тоді f(х) на цьому проміжку

а) спадає;

б) не спадає;

в) не зростає;

г) зростає; •

10. Яка з функцій має лінію точок розриву?

а) ;

б) ; •

в) ;

г) ;

11. Чому дорівнює ?

а) 1;

б) 0; •

в) не існує;

г) -1;

12. Нехай f – двічі диференційована функція, така, що f(0) =4, f(3) =5, f ′(3) =6. Чому дорівнює ?

а) 17; •

б) 18;

в) 12;

г) 9;

13. Чому дорівнює множина значень функції ?

а) [0;π/4]; •

б) [0;π/2];

в) [0;π/3];

г) [0;π/6];

14. Множиною значень функції у =х²+2х-3 є

а) [-4;+∞); •

б) (-∞;4];

в) (-∞;-4);

г) [4;+∞);

15. Яка найбільша потужність може бути у множини:

а) континуум;

б) злічена;

в) скільки завгодно велика; •

г) ;

16. Дослідити на збіжність за допомогою критерію Коші можна:

а) довільну збіжну послідовність;

б) довільну послідовність; •

в) тільки розбіжну послідовність;

г) тільки послідовність, що збігається до нуля;

17. Нехай f(х) неперервна в (а, b). Чи обов'язково

а) f(х) досягає sup f(х) в (а, b);

б) f(х) досягає sup f(х) на довільному (с, d) з (а, b);

в) f(х) обмежена в (а, b);

г) f(х) обмежена на довільному [c, d] з (а, b); •

18. Функція f називається обмеженою на Е, якщо

а) ; •

б)f(х) – неперервна на Е;

в) ;

г) ;

19. Дві послідовності збігаються. Тоді їх різниця є послідовність, яка

а) не обмежена зверху;

б) збігається; •

в) розбігається;

г) може як збігатись, так і розбігатись;

20. Не існує f ′ (х) в точці хо. Яке з тверджень вірне?

а) f(х) неперервна в точці х0;

б) f(х) розривна в точці х0;

в) f(х) необмежена в околі точки х0;

г) не існує ; •

21. В множині Е=(-3, 5) мінімальний елемент дорівнює

а) не існує; •

б) -3;

в) -2;

г) -2,9;

22. Відомо, що похідна функції у =f(х) на проміжку [2;5] дорівнює (-2х). Тоді f(х) на цьому проміжку

а) стала;

б) зростає;

в) спадає; •

г) не спадає;

23. А, В, С – три довільних множини. Яке з тверджень не є вірним?

а) ;

б) ;

в) ; •

г) ;

24. Яка з перерахованих властивостей функції у =3+lgх є вірною?

а) періодична;

б) у(1) =3; •

в) D(у) =R;

г) парна;

25. Яка послідовність має три часткових границі?

а) ; •

б) не має жодна;

в) (-1)ⁿ;

г) ;

26. Для функції точка - стаціонарна. Яка з умов достатня для того, щоб у цій точці не було екстремуму?

а) ;

б) ; •

в) ;

г) ;

27. Знайти кутовий коефіцієнт дотичної до графіка функції у = в точці х0 =π.

а) -1;

б) 1;

в) інша відповідь;

г) 0; •

28. Знайти .

а) 0,16;

б) -1;

в) -0,16; •

г) 1;

29. Нехай . Тоді g º f = :

а) х, х>0;

б) х²;

в) ‌‌‌‌‌‌│х│; •

г) 1/х²;

30. у =f(х) означена на (a;b). Яка з відповідей вірна?

а) ; •

б) ;

в) існує обернена функція;

г) існує ;

31. В множині Е=(-3, 5) мінімальний елемент дорівнює

а) інша відповідь;

б) не існує; •

в) -3;

г) 5;

32. Нехай послідовність {Xn} необмежена. Яке твердження вірне?

а) послідовність {Xn} є нескінченно великою;

б) послідовність {Xn} розбіжна; •

в) послідовність {Xn} є обмеженою знизу;

г) послідовність {Xn} монотонно зростає;

33. Яку з формул прийнято звати наближеною( при α – малому)?

а) sin(π/6+α)=cos(π/6);

б) sin(π/6+α)=1/2;

в) sin(π/6+α)=π/6-α; г) sin(π/6+α)=1/2+; •

34. Нехай . Тоді

а) точка а не належить до області визначення функції f(х);

б) точка а є точкою розриву першого роду для функції f(х);

в) точка а є усувною для функції f(х);

г) точка а є точкою розриву другого роду для функції f(х); •

35. Нехай функція g неперервна на відрізку [-2, 3] та . Яка найбільша кількість коренів g на цьому відрізку:

а) 3;

б) 2;

в) 1;

г) 4; •

36. Нехай . Тоді дорівнює:

а) ; •

б) ;

в) ;

г) ;

37. диференційована в точці . Який варіант відповіді невірний?

а) ; •

б) існують та у точці ;

в) ;

г) неперервна в точці

38. Матеріальна точка рухається з законом S(t)=sin(t) (t – в секундах, S – в метрах) по дійсній вісі. Тоді

а) швидкість точки буває більше 2 м/с;

б) в момент t=π сек. швидкість точки дорівнює (-1) м/с; •

в) через деякий час вона вийде за межі відрізка [-10; 10];

г) швидкість весь час додатна;

39. Нехай . Чому дорівнює ?

а) 1!+2!+3!+4!;

б) 1+2+3+4;

в) 0;

г) 4!; •

40. Довільна обмежена послідовність

а) має часткову границю; •

б) має скінчену границю;

в) має нескінченну часткову границю;

г) має нескінченну границю;

41. Похідна функції у = дорівнює

а) інша відповідь;

б) ;

в) ;

г) ; •

42. Довільна монотонна послідовність

а) має скінчену або нескінчену границю; •

б) зростає;

в) збігається;

г) обмежена;

43. Різниця яких двох ірраціональних чисел є число раціональне?

а) ; •

б) ;

в) ;

г) ;

44. Обчислити площу фігури, що обмежена лініями у =х; у =0; х =1.

а) 0,5;

б) інша відповідь;

в) 1;

г) 0,2; •

45. Функція f є багаточлен. Тоді вона

а)розкладається по ступеням лише бінома(х – 1);

б)розкладається по ступеням (х – х0), де х0 – довільне число; •

в)не розкладається в ступеневий ряд;

г)розкладається по ступеням 1/(х-1);

46. Яке з тверджень не гарантує диференційованість в точці ?

а) існує неперервний градієнт у точці ;

б) приріст функції можна записати так:

в) існують та у точці ; •

г) приріст функції можна записати так:

47. Чому дорівнює ?

а) ∞;

б) 1;

в) 5; •

г) 6;

48. Якщо функція f(х) неперервна в [а, b], то вона

а) монотонна на [а, b];

б) диференційована на [а, b];

в) має обернену на [а, b];

г) обмежена на [а, b]; •

49. В точці х одна функція диференційована, а інша має розрив. Тоді їх сума є функція, яка в цій точці

а) має розрив; •

б) двічі диференційована;

в) диференційована;

г) неперервна;

50. означає, що

а) ; •

б) ;

в) ;

г) ;

51. Функція f(х) неперервна на відрізку [0, 1] і f(0) =-f(1). Тоді

а) f(х) – має нуль в якійсь точці відрізка; •

б) f(х) – має нуль в точці х =1/2;

в) f(х) – стала на відрізку;

г) f(х) – розривна в кожній точці відрізка;

52. Якщо -1<<0, то ряд :

а) може як збігатись так і розбігатись;

б) розбігається;

в) збігається умовно;

г) збігається абсолютно; •

53. Знайти проміжки зростання функції у = 3х² - 6х + 7.

а) інша відповідь;

б) [1; +∞); •

в) (-∞; 1];

г) (-∞; 2];

54. . Яке з тверджень вірне?

а) f(х) – розривна в точці х0; •

б) f(х) – необмежена в околі точці х0;

в) f(х) – неперервна в точці х0;

г) f(х) – диференційована в точці х0;

55. Розкладання на найпростіші дробі має вигляд

а) ;

б) ;

в) ; •

г) ;

56. Нехай збігається рівномірно на множині Х. Яке твердження правильне?

а) - неперервна на Х;

б) - обмежена на Х;

в) - збігається;

г) ; •

57. Знайти найбільше значення функції f(х) = х² + 2х – 5 на відрізку [-2; 2].

а) -6;

б) 5;

в) 3; •

г) -5;

58. Чому дорівнює похідна n – го порядку функції у = sin х?

а) ;

б) ;

в) ; •

г) ;

59. Який з наступних рядів розбіжний?

а) ;

б) ; •

в) ;

г) ;

60. Яке натуральне число передує числу ?

а) серед наданих відповідей вірної не має;

б) такого числа не існує; •

в) 1;

г) 0;

61. Множина А є необмеженою тоді, та лише тоді, коли

а) ; •

б)

в) ;

г) ;

62. Диференціал функції в точці це:

а) похідна;

б) число;

в) квадратична функція;

г) лінійна функція; •

63. Ряд збігається при:

а) лише при х = 0;

б) усіх х; •

в) ;

г) ;

64. Матеріальна точка рухається прямолінійно за законом S(t)=, 0<t<1 (t – в секундах, S – в метрах). Знайти швидкість в момент часу t=3/4с.

а) 1/4 м/с;

б) 4 м/с;

в) 16 м/с; •

г) -4 м/с;

65. Яка послідовність не є нескінченно великою?

а) lg(ln n);

б) (-1)ⁿn;

в) ;

г) ; •

66. Нехай Х – універсальна множина.

а) ;

б) ; •

в) ;

г) ;

67. Нехай f(х) =О(g(х)) при х → а. Тоді

а) f(х)g(х) =о(1) при х → а;

б) f ≈ g при х → а;

в) g(х) =о(f(х)) при х → а;

г) ; •

68. Якщо <-1, то ряд :

а) розбігається; •

б) збігається умовно;

в) може як збігатись так і розбігатись;

г) збігається абсолютно;

69. Дотична до графіка функції в точці (0; 1) має вигляд

а) у =х;

б) х =1;

в) у =1; •

г) у =3х – 1;

70. Знайти рівняння дотичної до графіка функції у =(1/3)х³ - 2х² в точці х0=3.

а) у =3х – 1;

б) у =3х;

в) інша відповідь;

г) у =-3х; •

71. Яка з множин дійсних чисел обмежена лише зверху?

а) ;

б) ;

в) ;

г) ; •

72. Знайти критичні точки .

а) 2;

б) інша відповідь;

в) -2;2;0;

г) -2;2; •

73. Нехай . Тоді:

а) ;

б) збігається нерівномірно на ; •

в) ;

г) збігається рівномірно на ;

74. Яким числом є значення виразу ?

а) раціональним;

б) ірраціональним; •

в) інша відповідь;

г) від'ємним;

75. Яке з тверджень не гарантує диференційованість в точці ?

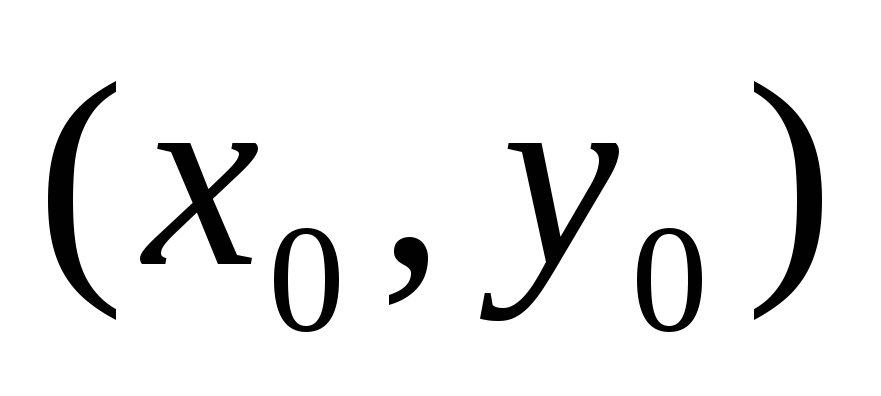а) існують та у точці ; •

б) існує неперервний градієнт у точці ;

в) приріст функції можна записати так: ;

г) приріст функції можна записати так: ;

76. Значення дорівнює

а) π/4;

б) (1/2)ln2; •

в) ln2;

г) π/8;

77. Якщо послідовність збігається, то

а) будь – яка її підпослідовність збігається; •

б) будь – яка її підпослідовність монотонна;

в) вона необмежена;

г) вона має необмежену підпослідовність;

78. Функція у = f(х) інтегрована на [а, b]. Чи обов'язково вона

а) обмежена на [а, b]; •

б) монотонна на [а, b];

в) неперервна на [а, b];

г) диференційована на (c; d) [а, b];

79. При яких х графік перетинає вісь абсцис?

а) х =1; •

б) х =±1;

в) х =0;

г) х =0.5;

80. Нехай а>0. Тоді

а) π;

б) +∞;

в) е;

г) 0; •

81. Якщо послідовність є нескінченно великою, то вона:

а) ;

б) необмежена; •

в) ;

г) зростає;

82. Найменший додатний період функції у =sin 3х дорівнює

а) 2π;

б) 3π;

в) 2π/3; •

г) π/3;

83. Для функції точка - стаціонарна. Яка з умов достатня для того, щоб у цій точці не було екстремуму?

а) ;

б) ;

в) ; •

г) ;

84. Точками перетину функції у =cos х з віссю OX є

а) ; •

б) ;

в) ;

г) ;

85. Знайти критичні точки функції .

а) інша відповідь;

б) 1;

в) -1, 1;

г) 1, 0; •

86. Нехай функція f(х) інтегрована на [а, b], g(х) – монотонна на [a;b]. Яке твердження правильне?

а) (f(х)/g(х)) інтегрована на [а, b];

б) f(х)∙g(х) інтегрована на [а, b]; •

в) f(х)∙g(х) монотонна на [а, b];

г) f(х)+g(х) монотонна на [а, b];

87. Дотична площина до поверхні в точці (0, 0, 0) має рівняння:

а) ;

б) ;

в) ; •

г) ;

88. Нехай f(х) =o(х), g(х) =o(х³), коли х→0. Що вірно?

а) ; •

б) ;

в) ;

г) ;

89. диференційована в точці . Який варіант відповіді невірний?

а) існують та у точці ;

б) ;

в) неперервна в точці

г) ; •

90. Чи може необмежена на множині функція бути неперервною на , якщо:

а) ; •

б) ;

в) ;

г) ;

91. Послідовність є

а) обмеженою; •

б) необмеженою;

в) нескінченно великою;

г) нескінченно малою;

92. Похідна функції у =ln(х²) дорівнює

а) ;

б) ; •

в) ;

г) ;

93. дорівнює

а) 1/5; •

б) 0;

в) ∞;

г) 5;

94. Функція необмежена і неперервна. На якій з областей вона визначена?

а) ;

б) ;

в) ; •

г) ;

95. Дотична площина до поверхні в точці (0, 0, 0) має рівняння:

а) ; •

б) ;

в) ;

г) ;

96. Яким числом є значення виразу ?

а) інша відповідь;

б) ірраціональним;

в) додатним;

г) раціональним; •

97. Функція f(х) в околі точки х =х0 монотонно зростає. Яке з тверджень вірне?

а) f(х) неперервна в точці х0;

б) , де U(х0, δ) – окіл точці х0;

в) f(х) диференційована в точці х0;

г) ; •

98. Нехай a ≠ 0. Яким чином треба до визначити функцію в точці х = 0, щоб вона була неперервною?

а) a/2;

б) f(х) має розрив в точці х = 0 при будь – якому f(0);

в) 0;

г) a²/2; •

99. Нехай функція f(х) інтегрована на [а, b]. Чи обов'язково вона

а) неперервна на [a;b];

б) диференційована на (c;d) [a;b];

в) обмежена на [a;b]; •

г) монотонна на [a;b];

100. Нехай {αn} та {βn} нескінченно малі послідовності, αn ≠ 0. Яке твердження вірне?

а) послідовність є нескінченно великою;

б) послідовність є нескінченно малою;

в) послідовність є нескінченно малою;

г) послідовність , де с =const ≠0 є нескінченно великою; •

101. Знайти проміжки спадання функції у = -х² + 2х – 3.

а) [1; +∞); •

б) (-∞; +∞);

в) інша відповідь;

г) (-∞; 1];

102. Ряд збігається при:

а) p>1;

б) всіх р; •

в) завжди розбігається;

г) р<1;

103. Маємо два означених інтеграла та . Тоді

а) другий інтеграл від'ємний;

б) більшим є другий інтеграл; •

в) інтеграли рівні;

г) перший з інтегралів більше другого;

104. - точка локального максимуму для . Яке з тверджень вірне?

а) - не диференційована у точці ;

б) - означена у точці ; •

в) диференційована в точці

г) = 0, = 0 у точці ;

105. Ряд збігається при:

а) р<1;

б) завжди розбігається;

в) всіх р; •

г) p>1;

106. Сума двох рядів, що збігаються , є ряд який:

а) може як збігатись, так і розбігатись;

б) розбігається;

в) збігається; •

г) абсолютно збігається;

107. Нехай Y – множина значень послідовності. Тоді

а) Y може складатись з одного елемента; •

б) Y має хоча б одну точку границі;

в) Y може складатись з довільного раціонального числа елементів;

г) Y – обмежена;

108. Нехай у = f(х) неперервна зліва в точці х0. Яка з відповідей вірна?

а) ; •

б) ;

в) ;

г) ;

109. Нехай . Тоді f ◦ g = :

а) х, х>0; •

б) х²;

в) ‌‌‌‌‌‌│х│;

г) 1/х²;