гл4

40

4. МИНИМИЗАЦИЯ БУЛЕВЫХ ФУНКЦИЙ

Отметим, что реально формуле соответствует соединение элементов, реализующих исходные функции (логическая схема). Каждой формуле соответствует своя логическая схема (см. гл. 8).

Например, функция штрих Шеффера может быть представлена двумя формулами над множеством связок 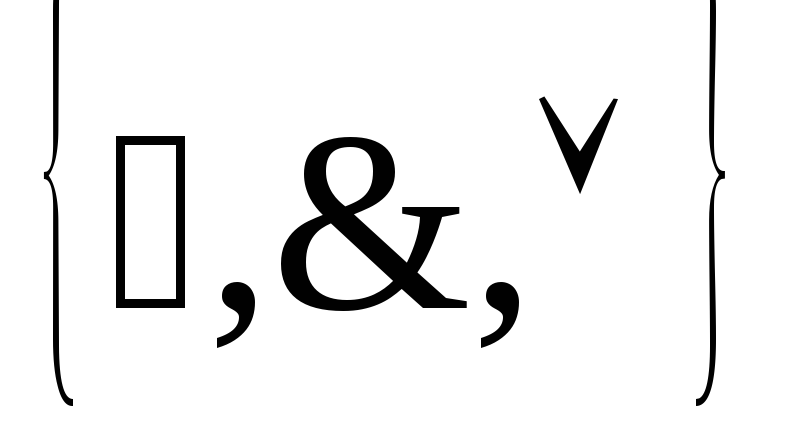: и . Первой формуле соответствует схема, представленная на рис.4.1, второй – на рис.4.2¹⁾. Схема, соответствующая второй формуле, содержит на один элемент меньше, чем схема, соответствующая первой формуле, следовательно, она более предпочтительна. Задача поиска формулы, соответствующей наиболее простой схеме (задача минимизации логической функции), представляет большой практический интерес.

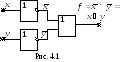
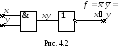
Общая задача минимизации может быть сформирована следующим образом: найти аналитическое выражение заданной логической функции в форме, содержащей минимально возможное число связок. Следует отметить, что в общей постановке данная задача пока не решена, однако, достаточно хорошо исследована для булевых функций в классе дизъюнктивно-конъюнктивных нормальных форм.

Дадим основные определения.

Элементарной конъюнкцией называется конъюнкция конечного числа различных между собой логических переменных, каждая из которых может иметь или не иметь отрицания.

Рангом элементарной конъюнкции называется число переменных в данной конъюнкции.

Дизъюнктивной нормальной формой (ДНФ) называется дизъюнкция элементарных конъюнкций.

Минимальной дизъюнктивной формой (МДНФ) логической функции называется ДНФ, содержащая наименьшее число букв (по отношению ко всем другим ДНФ, представляющим заданную логическую функцию).

Логическая функция называется импликантом функции , если для всякого набора значений аргументов выполнено неравенство . Это условие может быть эквивалентно переписано в виде

.

Импликант называется простым, если он представляет собой конъюнкцию переменных (возможно, с отрицаниями) и любая конъюнкция, получаемая из него в результате вычеркивания каких-либо переменных, импликантом не является.

В качестве примера рассмотрим функцию

.

Функция является импликантом, ибо

(мы воспользовались соотношением .

Поскольку не есть конъюнкция, импликант не простой. Конъюнкция также является импликантом. Если из нее вычеркнуть переменную , полученная конъюнкция снова будет импликантом, ибо

Отсюда следует, что импликант не является простым. Легко проверить, что конъюнкции и , полученные из вычеркиванием одной переменной, импликантами не будут. Поэтому представляет собой простой импликант.

Утверждение. Любая логическая функция эквивалентна дизъюнкции всех своих простых импликантов.

Дизъюнкция всех простых импликантов логической функции называется ее сокращенной ДНФ.

Приведенное утверждение ясно, если рассмотреть геометрическую интерпретацию логической функции в виде гиперкуба. В этом случае можно дать следующее определение импликанта. Функция является импликантом для , если соответствующее ей множество вершин куба содержится во множестве вершин для . Всякая конъюнкция задает подкуб, представляющий собой множество вершин , для которых , а значения остальных компоненты могут быть выбраны произвольно. Подкуб, соответствующий конъюнкции длины , содержит вершин. В частности, подкуб для конъюнкции длины вырождается в вершину. На рис. 4.3 заштрихован подкуб, соответствующий конъюнкции (он представляет собой грань ). Простой импликант определяет подкуб, все вершины которого принадлежат множеству единичных вершин функции, и такой, что он не содержится ни в каком большем подкубе, обладающем этим свойством. Такие подкубы называют максимальными. Всякая ДНФ задает покрытие множества единичных вершин функции подкубами, соответствующими ее конъюнкциям. Всякая сокращенная ДНФ задает покрытие множества единичных вершин функции максимальными подкубами. На этом языке данное утверждение становится очевидным.

Сокращенная ДНФ логической функции называется тупиковой, если в ней отсутствуют лишние простые импликанты.

Устранение лишних простых импликантов из сокращенной ДНФ логической функции не является однозначным процессом, т.е., логическая функция может иметь несколько тупиковых форм. Тупиковые ДНФ, содержащие минимальное число букв, являются минимальными. Минимальных ДНФ логической функции тоже может быть несколько.

Все методы минимизации практически отличаются лишь на первом этапе – этапе получения сокращенной ДНФ. Второй этап - получение минимальной (или одной из тупиковых) ДНФ идентичен для всех методов.

В данной главе будут рассмотрены два метода минимизации полностью определенных функций и метод минимизации частичных функций. Все методы функционируют в классе ДНФ. Путем применения принципа двойственности эти методы могут быть обобщены для КНФ.

4.1. Метод Квайна

Метод Квайна основан на применении двух соотношений.

а) соотношение склеивания

;

б) соотношение поглощения

,

справедливость обоих соотношений была доказана в гл. 2.

1 ЭТАП. Получение сокращенной ДНФ.

Рассмотрим некоторый импликант функции , являющийся конъюнкцией. Для удобства будем считать, что в него входят первые переменных, т.е., импликант имеет вид .

На всех наборах (при различных ) импликант равен 1. Поэтому, функция на этих наборах также обращается в 1, и в ее СДНФ присутствуют всевозможные конъюнкции вида .

Осуществив склеивания по переменной ,

,

из них можно получить всевозможные конъюнкции вида . Затем, произведя склеивания по переменной , придем к всевозможным конъюнкциям и т.д., пока не получим .

Таким образом, всякий импликант, имеющий вид конъюнкции, можно получить из конъюнкций СДНФ последовательным применением операции склеивания. Легко видеть, что верно и обратное: всякая конъюнкция, полученная таким образом, является импликантом.

Отсюда можно сделать вывод, что все импликанты, имеющие вид конъюнкций, и только они, могут быть образованы в результате последовательного склеивания конъюнкций из СДНФ.

Пример 4.1. Пусть функция задана в СДНФ

.

Получим все простые импликанты функции . Для этого необходимо произвести все возможные склеивания сначала конституент, а затем всех производных конъюнкций более низкого ранга и выполнить все возможные поглощения. Этот процесс иллюстрирует табл. 4.1. Таблица состоит из трех колонок, которые заполняются последовательно. В колонке 1 помещены конституенты единицы. Каждая конституента помечена номером (1-7). В колонке 2 содержатся конъюнкции ранга 3 (номера 8-13), полученные в результате проведения всех возможных склеиваний конституент. Если и конституенты склеились, используется запись , где – результат склеивания. Конституенты, поглощаемые конъюнкциями колонки 2, помечаются значком . В колонке 3 находятся конъюнкции ранга 2, полученные путем проведения всех возможных склеиваний конъюнкций из колонки 2. Поглощаемые ими конъюнкции из колонки 2 отмечаются значком . Конъюнкции из колонки 3 не склеиваютя. Конституенты и конъюнкции более низкого ранга, не участвовавшие в склеивании (не отмеченные значком ), являются простыми импликантами, образующими сокращенную ДНФ функции

Таблица 4.1

1			2			3
1)			8)			15)
2)			9)			16)
3)			10)
4)			11)
5)			12)
6)			13)
7)			14)

2 ЭТАП. Получение минимальной (или одной из тупиковых) ДНФ.

Для получения МДНФ необходимо убрать из сокращенной ДНФ все лишние простые импликанты. Это делается с помощью специальной импликантной матрицы Квайна. Строки такой матрицы отмечаются простыми импликантами, т.е., членами сокращенной ДНФ, а столбцы - конституентами единицы, т.е., членами СДНФ логической функции. Если простая импликанта поглощает некоторую конституенту единицы, то соответствующая клетка матрицы Квайна, на пересечении строки с рассматриваемой простой импликантой, и столбца с конституентой единицы отмечается значком – *. Минимальные ДНФ строятся по импликантной матрице следующим образом:

1. ищутся столбцы импликантной матрицы, имеющие одну *. Соответствующие этим * простые импликанты называются базисными и составляют так называемое ядро логической функции. Ядро обязательно входит в МДНФ.

2. рассматриваются различные варианты выбора совокупности простых импликантов, которые накроют остальные столбцы импликантной матрицы, и выбираются варианты с минимальным суммарным числом букв в такой совокупности импликантов.

Пример 4.1 (продолжение).

Импликантная матрица представлена табл.4.2. Ядром нашей функции являются импликанты , , . Импликант – лишний, т.к. ядро накрывает все столбцы импликантной матрицы. Поэтому, функция имеет единственную тупиковую и минимальную ДНФ

Таблица 4.2

Простые импли-канты	Номера конституент единицы
	1	2	3	4	5	6	7
	*	*	*	*
				*			*
						*	*
	*				*

Пример 4.2. Минимизировать булеву функцию методом Квайна:

1. Получим функцию в СДНФ

2. Найдем сокращенную ДНФ функции f, произведя все возможные склеивания и поглощения:

3. Получим МДНФ функции по импликантной матрице (табл. 4.3). Ядро булевой функции: . Функция имеет две тупиковые ДНФ. Они же являются минимальными ДНФ

Таблица 4.3

Простые импли-канты	Конституенты
	*	*
		*			*
	*		*
			*	*

При программной реализации метода Квайна конъюнкции, подлежащие склеиванию, разбивают на группы. В i-ю группу включают конъюнкции, содержащие i переменных без отрицания. Тогда на склеивание нужно проверять только конъюнкции соседних групп, при этом перебор сокращается. Сами конъюнкции удобно кодировать двумя двоичными векторами (вектор вхождения) и (вектор обращения), элементы которых определяются следующим образом:

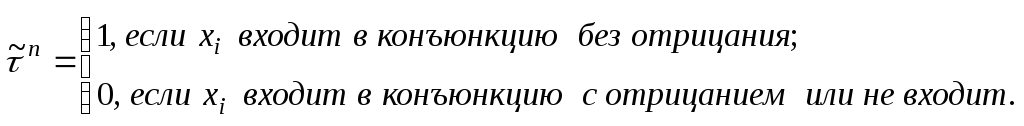
Например, конъюнкция может быть сохранена с помощью векторов и . Данные вектора удобно хранить в битовой форме.

При большом числе аргументов наиболее трудоемким является этап, связанный с отысканием наилучшего покрытия импликантной матрицы (сокращенная ДНФ и сама матрица находятся сравнительно быстро). Поэтому, для осуществления этого этапа обычно используют приближенные методы, не гарантирующие нахождения МДНФ. Один из таких методов состоит в следующем:

1. Ищется ядро логической функции. Столбцы, покрытые ядром, вычеркиваются из таблицы.

2. Дальнейший выбор импликантов осуществляется с использованием следующей пошаговой процедуры. В новой таблице берется строка с наибольшим числом символов * (если таких строк несколько, то любая из них). Эта строка и столбцы, в которых она содержит * из таблицы вычеркиваются, а соответствующий ей импликант включается в покрытие. К полученной таблице применяется та же операция и т.д., пока все столбцы не окажутся вычеркнутыми.

Если требуется нахождение всех тупиковых ДНФ (всех покрытий импликантной матрицы), то можно воспользоваться следующим методом (метод Петрика). По импликантной матрице строится так называемое конъюнктивное представление матрицы. Для этого все строки (простые импликанты) обозначаются разными буквами. После этого, для каждого i-го столбца матрицы строится дизъюнкция всех букв, обозначающих строки матрицы, пересечение которых с i-м столбцом отмечено *. Конъюнктивное представление матрицы образуется как конъюнкция построенных дизъюнкций для всех столбцов матрицы. К конъюнктивному представлению матрицы могут быть применены все соотношения булевой алгебры с целью его упрощения. После раскрытия скобок и выполнения всех возможных поглощений получается дизъюнкция конъюнкций, каждая из которых соответствует покрытию матрицы, т.е, тупиковой ДНФ функции.

Пример 4.3. Импликантная матрица функции задана табл.4.3. Найти методом Петрика все тупиковые ДНФ функции . Имеющиеся простые импликанты обозначим буквами:

Тогда конъюнктивное представление матрицы имеет вид

После упрощения получим Т.о., функция имеет две тупиковые ДНФ:

4.2. Метод Блейка-Порецкого

Метод позволяет получать сокращенную ДНФ булевой функции f из ее произвольной ДНФ. Базируется на применении формулы обобщенного склеивания: .

В основу метода положено следующее утверждение: если в произвольной ДНФ логической функции произвести все возможные обобщенные склеивания, а затем выполнить все поглощения, то в результате получится сокращенная ДНФ функции .

Пример 4.4. Логическая функция f задана произвольной ДНФ