гл3

29

3. СПЕЦИАЛЬНЫЕ ВИДЫ ФОРМУЛ

В гл. 1 и 2 уже рассматривалось аналитическое представление логических функций в виде формул. В данной главе будут рассмотрены универсальные (канонические) формы представления, дающие возможность получить форму непосредственно по таблице истинности для произвольной логической функции. Эта форма в дальнейшем может быть упрощена (минимизирована). Вопросы минимизации логических функций и их систем будут рассмотрены в дальнейшем (гл. 4,5,6).

3.1. Разложение функции по переменным. Представление логических функций бинарным графом

Пусть – логическая переменная. При введем обозначение

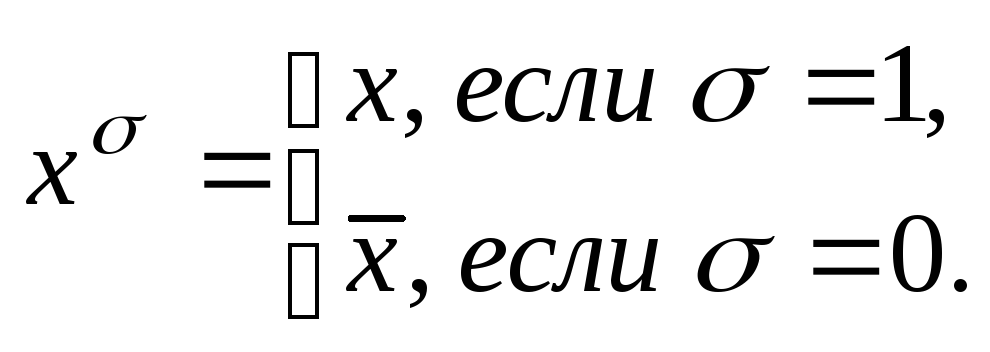
Легко проверить, что , тогда и только тогда, когда . Следовательно, конъюнкция – равна 1 на единственном наборе значений аргументов , ,,.

Следующая теорема позволяет выразить функцию через функции от меньшего числа аргументов.

Теорема 3.1 (о разложении функций).

Всякая логическая функция при любом может быть представлена в виде:

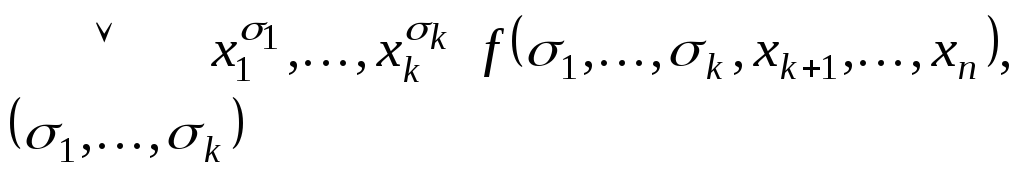(3.1)

где дизъюнкция берется по всевозможным наборам значений аргументов . Например, при ,

.

Доказательство: Убедимся, что для любого набора значений аргументов левая и правая части формулы принимают одинаковые значения. Поскольку , при и , то

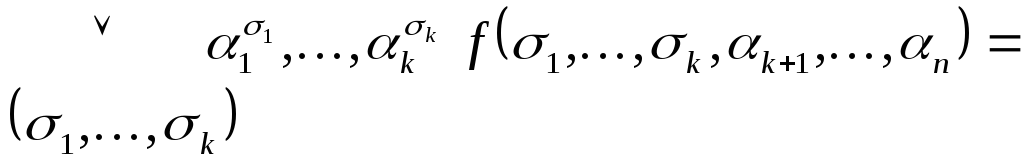
Эта величина совпадает со значением левой части. Теорема доказана.

Представление функции в виде (3.1) называется разложением по переменным (разложением Шеннона). Переменные называются переменными разложения или переменными исключения.

Частный случай разложения Шеннона при имеет вид:

(3.2)

Используя формулу (3.2), можно представить логическую функцию в виде бинарного графа, в котором имеется ровно одна вершина без входящих в нее дуг (начальная); все вершины, по числу выходящих дуг, делятся на два типа: вершины с двумя выходящими дугами (условные вершины), вершины без выходящих дуг (заключительные вершины). Дуги помечаются символами 0 и 1. Условные вершины помечаются символом переменной, заключительные – комадой "".

Пример БГ для функции приведен на рис. 3.1. Здесь вершины – начальная; , и - условные; и – заключительные.

Каждому набору значений аргументов в БГ соответствует путь из начальной вершины в заключительную. Таким образом, БГ каждому набору значений аргументов ставит в соответствие значение функции и может служить для ее задания и вычисления. Разным наборам может соответствовать один и тот же путь. Например, для графа, изображенного на рис.3.1, наборам и соответствует путь . Алгоритм построения БГ представлен структурограммой на рис.3.2.

Вводим исходную функцию
,
Вводим начальную вершину и приписываем ей логическую функцию
	, ?
	ДА					НЕТ
	Помечаем вершину командой "" и объявляем ее заключительной.	Выбираем переменную разложения для функции . Вершину помечаем буквой .
			Получаем остаточную функцию
			Среди вершин графа ищем вершину для кото- рой . Текущее число вершин графа равно .
			Вершина найдена ?
			ДА		НЕТ
			Вводим дугу и помечаем ее символом .
					Вводим новую вершину и дугу . Вершине приписываем логическую функцию , дугу помечаем символом .
				ПОВТОРЯТЬ до
	ПОВТОРЯТЬ до
Удаляем логические функции, приписанные вершинам бинарного графа.
Выводим бинарный граф

Рис. 3.2

Следует отметить, что всякую логическую функцию, заданную булевой формулой F, содержащей N букв, можно представить БГ, содержащим N условных вершин. Однако, сложность остаточных функций, а, следовательно, и число условных вершин в БГ зависит от порядка исключения переменных. Так, если в функции на первом ярусе исключить переменную , то получится БГ (рис. 3.3), содержащий три условные вершины, т.е., на одну меньше, чем БГ той же функции полученный ранее (см. рис. 3.1). Число всевозможных способов исключения переменных растет комбинаторно. Например, если на каждом ярусе БГ будет исключаться одна и та же переменная, то это число равно , но на каждом ярусе можно исключать и различные переменные. Поэтому, выбор оптимального исключения перебором всех способов исключения – трудоемкий процесс. Оптимальное исключение переменных ищут, используя эвристические критерии, один из которых будет рассмотрен в главе 8.3.

3.2. Совершенная дизъюнктивная и конъюнктивная нормальные формы

Воспользовавшись теоремой 3.1 при , получаем представление

,

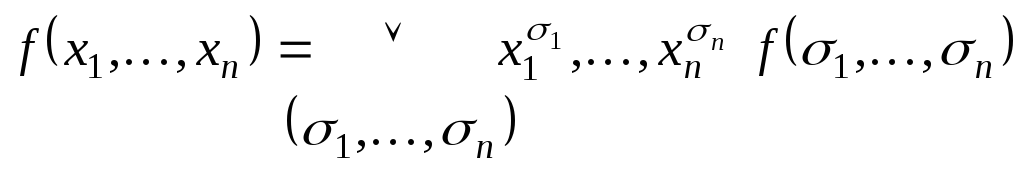которое для может быть преобразовано к виду

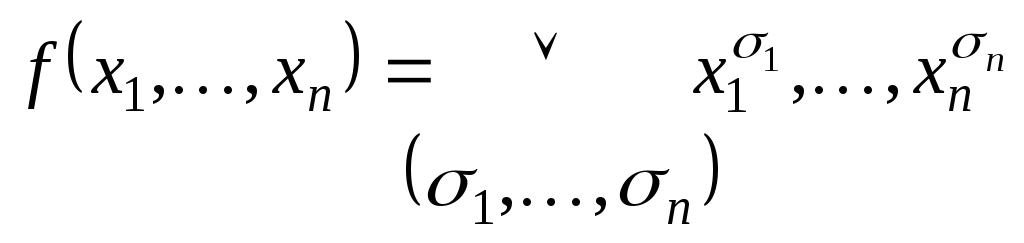, (3.3)

где дизъюнкция берется по всем наборам , на которых .

Разложение функции по всем переменным (3.3) называют предельным разложением Шеннона или совершенной дизъюнктивной нормальной формой (СДНФ) функции . СДНФ функции содержит ровно столько конъюнкций, сколько единиц в таблице функции , каждому единичному набору соответствует конъюнкция всех переменных, в которых взято с отрицанием, если , и без отрицания, если . Например, набору соответствует конъюнкция =. Такую конъюнкцию еще называют конституентой единицы. Другими словами, СДНФ – это дизъюнкция конституент единицы, соответствующих единичным наборам функции.

Таблица 3.1
0 0	1	0	0
0 1	1	1	0
1 0	1	1	1
1 1	0	0	0

Таким образом, существует взаимно однозначное соответствие между таблицей функции и ее СДНФ, и, следовательно, СДНФ для всякой логической функции единственна (точнее, единственна с точностью до порядка букв и конъюнкций: это означает, что ввиду коммутативности дизъюнкции и конъюнкции, формулы, полученные из (3.3) перестановкой конъюнкций и букв в конъюнкции, не различаются и считаются одной и той же СДНФ). Например, функции, заданные табл. 3.1, имеют СДНФ:

,

,

.

Единственная функция, не имеющая СДНФ – это константа 0.

Теорема 3.2. Всякая логическая функция может быть представлена булевой формулой, то есть, как суперпозиция дизъюнкции, конъюнкции и отрицания.

Доказательство: Как было сказано выше, всякую логическую функцию, кроме константы 0, можно представить СДНФ, которая является булевой формулой. Константу 0 можно представить в виде булевой формулы . Таким образом, любую логическую функцию можно представить булевой формулой. Теорема доказана.

Так как СДНФ для логической функции единственна, то иногда, для установления эквивалентности формул удобно формулы привести с СДНФ и произвести их сравнение.

Пример 3.1. Эквивалентны ли формулы и ?

Формула является СДНФ, так как представляет собой дизъюнкцию двух конституент единицы. По определению эквивалентности ( в табл. 1.6) получим ее представление в СДНФ: . Используя представление эквивалентности в СДНФ и соотношения булевой алгебры, преобразуем в СДНФ :

,

т. е. формулы и эквивалентны.

Используя принцип двойственности, выпишем двойственное предельное разложение Шеннона:

,

,

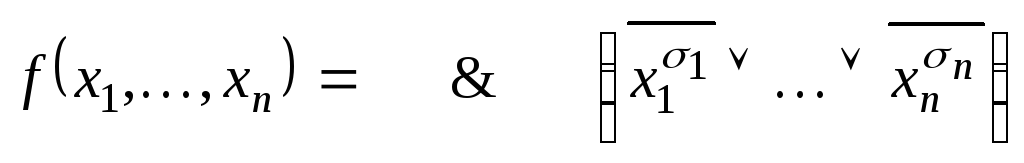которое называется совершенной конъюнктивной нормальной формой (СКНФ) функции . СКНФ функции содержит ровно столько дизъюнкций, сколько нулей в таблице функции , каждому нулевому набору соответствует дизъюнкция всех переменных, в которых взято без отрицания, если , и с отрицанием, если . Например, набору соответствует дизъюнкция . Для такой дизъюнкции еще употребляется название конституента нуля. То есть СКНФ представляется как конъюнкция конституент нуля, соответствующих нулевым наборам функции. Следовательно, между таблицей и СКНФ также существует взаимно однозначное соответствие. Например, функции, заданные табл.3.1, имеют СКНФ:

,

,

.

3.3. Совершенная полиномиальная нормальная форма. Полином Жегалкина. Линейные функции

Пусть функция представлена в СДНФ , где , различны. По соотношению (2.20) . Однако конъюнкция двух различных конституент единицы и равна 0, так как , по крайней мере для одного , и тогда и, следовательно, . Т.о., . Из данной формулы следует, что в СДНФ можно заменить операцию дизъюнкции операцией сумма по модулю 2. Такая форма называется совершенной полиномиальной нормальной формой (СПНФ).

Пример 3.2. Получить СПНФ функции .

Для получения СПНФ представим функцию в СДНФ:

Тогда в СПНФ функция запишется в следующем виде:

Если в произвольной формуле алгебры Жегалкина раскрыть скобки по правилу (2.16) и произвести все возможные упрощения по соотношениям (2.17) и (2.18), то получится формула, имеющая вид суммы произведений, то есть, полинома по модулю 2. Такая формула называется полиномом Жегалкина. Полином Жегалкина имеет вид

, (3.4)

где .

Переход от СПНФ к полиному показан в примере 3.3,1. Любая булева формула также может быть преобразована к полиному – пример 3.3,2.

Пример 3.3. Получить полином Жегалкина функции .

1. В СПНФ функция представляется следующим образом (см. пример 3.2) . Избавимся от отрицаний, используя соотношение (2.19):

.

Раскрыв скобки и применив формулы (2.17) и (2.18), получим

2. Используя формулы (2.20) и (2.19), получаем

Раскрыв скобки, и применив формулы (2.17) и (2.18), получим

Для получения полинома из произвольной формулы сначала, обычно, строят эквивалентную формулу над множеством связок , а затем, получают из нее полином.

Пример 3.4. Получить полином Жегалкина функции .

Как и в примере 3.1, здесь использовалось определение элементарных функций. Импликация ( в табл. 1.6) была представлена в СКНФ:

Если полином Жегалкина функции имеет вид

,

то функция называется линейной.

Пример 3.5. Определить, является ли функция линейной:

Таким образом, в полиноме функции отсутствуют конъюнкции переменных, следовательно, функция линейна. В предыдущем примере, в полиноме функции присутствовала конъюнкция переменных и , т.е. – нелинейная функция.

Теорема 3.3. Для всякой логической функции существует полином Жегалкина, и притом единственный.

Доказательство: Существование полинома уже доказано. Для доказательства единственности, покажем, что между множествами всех функций от переменных и множеством всех полиномов Жегалкина от переменных существует взаимно однозначное соответствие. Число различных членов (то есть конъюнкций переменных) полиномов от переменных равно числу всех подмножеств из элементов, то есть (пустому подмножеству соответствует член 1). Число различных полиномов, которые можно образовать из этих конъюнкций, равно числу всех подмножеств множества конъюнкций, то есть (пустому подмножеству конъюнкций соответствует полином 0). Таким образом, число всех полиномов Жегалкина от переменных равно числу всех функций от переменных. Так как разным функциям соответствуют разные полиномы (одна и та же формула не может представлять две разные функции), то, тем самым, между множествами функций и полиномов от переменных установлено взаимное однозначное соответствие, что и доказывает единственность полинома для каждой функции. Теорема доказана.

На основании теоремы 3.3 можно проверять эквивалентность формул. Для этого, каждую формулу преобразуют в полином Жегалкина и производят сравнение полученных полиномов.

Задания для самостоятельной работы

3.1. Получить булевы формулы для функций: , , .

3.2. С помощью эквивалентных преобразований привести к ДНФ формулу:

;

;

.

3.3. Представить в виде совершенной ДНФ следующие функции:

; .

3.4. С помощью преобразований вида , перейти от заданной ДНФ к совершенной, если: