77

Число состояний характеризует "память" устройства. В частности, если устройство может находиться лишь в одном фиксированном состоянии, то значения его выходов не зависят от предыстории и однозначно определяются значениями входов. Такое устройство памятью не обладает.

Если входным и выходным алфавитами устройства без памяти являются {0,1}, то оно реализует на своих выходах систему логических функций

…

.

Говорят, что система логических функций является моделью дискретного устройства без памяти с входным и выходным алфавитом {0,1}¹⁾. Причем, такая модель не учитывает внутреннюю структуру устройства и задержку срабатывания.

В реальном устройстве наборы значений переменных соответствуют состояниям некоторых физических величин. Часто эти значения бывают согласованными, и поэтому, в процессе функционирования устройства некоторые наборы никогда не встретятся. То, как ведет себя устройство в этих случаях, оказывается несущественным. Работа таких устройств описывается частичными логическими функциями, (устройство имеет один выход) или их системами (устройство имеет несколько выходов). Частичные функции могут возникнуть и при синтезе всюду определенных устройств. Если, например, выходная функция устройства представлена в виде и функция уже реализована, то значение функции на тех наборах, где , может выбираться произвольно.

Физическая (аппаратная) реализация дискретных устройств обычно осуществляется с помощью логических схем. Логические схемы, реализующие дискретные устройства без памяти, называются комбинационными. В дальнейшем имеются в виду только такие схемы.

Каждой формуле, представляющей логическую функцию, соответствует логическая схема. Схемы, которые адекватно¹⁾ описываются формулами, называются схемами без ветвлений, то есть, в таких схемах выход каждого элемента используется не более одного раза (к нему подсоединено не более одного входа не более чем одного элемента схемы). Синтез оптимальных схем такого вида сводится к минимизации функций.

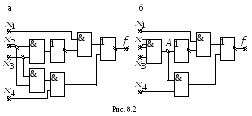
Проблема минимизации сама по себе довольно трудна, однако она не исчерпывает всех возможностей минимизации схем. Дальнейшее упрощение схем достигается за счет использования ветвлений - к выходу некоторого элемента Е подключается k_E, k_E<1 входов²⁾. Схема с ветвлениями не может быть адекватно описана формулой. Например, схема на рис 8.2,б реализует ту же функцию , что и схема на рис.8.2,а, однако схема "б" проще, чем схема, соответствующая любой формуле в булевом базисе. Схема "б" содержит ветвления в узле A. В гл.6, при рассмотрении минимизации систем функций, упрощение схемы, реализующей систему, также достигалось за счет использования ветвлений (рис.6.1).

Из сказанного следует, что в общем случае задача поиска оптимальных схемных решений требует большого перебора и практически не реализуема. Достаточно точно оценить по данной функции число элементов в минимальной схеме, не проводя синтеза, также не удается. Поэтому, на практике синтез схем осуществляется приближенными методами, дающими удовлетворительный результат. Два таких метода будут рассмотрены в данной главе. Более подробно методы синтеза см. в [3, c.85-93], [4, c.231-259]).

Теоретические исследования задачи синтеза пошли по пути поиска глобальных характеристик сложности схем. Основной результат здесь формулируется следующим образом.

Пусть - число элементов минимальной схемы в базисе, реализующей функцию f. Обозначим , где максимум берется по всем функциям от n переменных (множество всех функций от n переменных обозначено ). Функция называется функцией Шеннона для базиса , она равна минимальному числу элементов из , достаточному для реализации любой функции из .

Теорема 8.1 (теорема Шеннона-Лупанова).

Для любого базиса

,

где - константа, зависящая от базиса, причем для любого доля функций f, для которых , стремится к нулю с ростом n.

Здесь знак “~” обозначает асимптотическое равенство (a(n)~b(n), если ). Смысл второго утверждения теоремы в том, что с ростом n почти все функции реализуются со сложностью, близкой к верхней границе, т.е. .

Аналогичные характеристики получены и для систем функций [3, с.107 ].

8.2. Метод непосредственного моделирования связок , , с помощью связок заданного базиса

Рассматриваемый метод позволяет синтезировать схемы без ветвлений в заданном базисе и состоит в следующем.

1. Для заданной логической функции находят ее оптимальную, в смысле количества связок , скобочную форму, то есть, находят абсолютно минимальную форму в булевом базисе. Так как такая задача является очень трудоемкой, то вместо абсолютно минимальной формы логической функции на практике используют выходную форму факторного алгоритма (см. гл. 5).

2. Выражают связки в виде суперпозиции связок заданного базиса.

3. Подставляют результаты п.2 в выражение, полученное в п.1, отмечая стыки блоков, моделирующих в заданном базисе.

4. Анализируя стыки, устраняют избыточность логической схемы, используя закон двойного отрицания.

Пример 8.1. Синтезировать логическую схему, реализующую функцию в импликантном базисе .

1. Минимизируя функцию, получим .

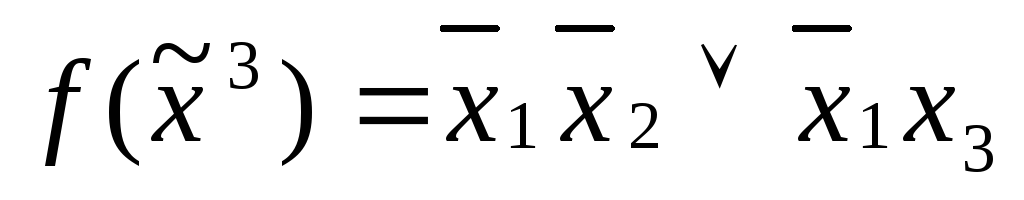В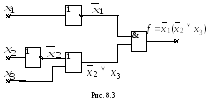ыполнив процесс факторизации, получим . Соответствующая схема приведена на рис.8.3.

2. Выражаем связки через связки импликантного базиса:

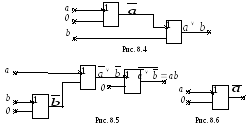
Схемы в базисе , эквивалентные , представлены на рис. 8.4, 8.5, 8.6 соответственно.

3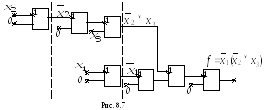. Заменяя элементы схемы, полученной в п.1 (рис.8.3), эквивалентными в п.2 (рис.8.4, 8.5, 8.6), получим схему на рис.8.7.

4. Анализируем стыки блоков. В базисе закон двойного отрицания можно изобразить так, как показано на рис. 8.8.

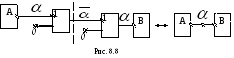
У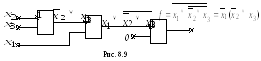страняя избыточность логической схемы, изображенной на рис.8.7, используя закон двойного отрицания (рис.8.8), окончательно получим схему, реализующую исходную логическую функцию в базисе (рис.8.9).

Пример 8.2. Синтезировать логическую схему из двухвходовых элементов "И", "ИЛИ" и инверторов, реализующую функцию , представленную своей МДНФ:

.

Получим скобочную форму функции путем применения факторного алгоритма для ее МДНФ:

В данном случае, заданные элементы реализуют булевы операции. Соответствующая схема приведена на рис. 8.10.

8.3. Метод каскадов

Метод каскадов, основанный на разложении функции (3.1), (3.2), позволяет при наличии блоков исключения переменных свести реализацию логической функции от n переменных к реализации функции от n-k () переменных. Размерность остаточных функций , в свою очередь, можно понизить, исключая t переменных и т.д. до тех пор, пока остаточные функции не будут иметь простой вид, и их реализация в заданном базисе не будет представлять трудностей.

Например, при использовании блоков исключения одной переменной, реализацию логической функции можно свести к реализации функции двух переменных, что иллюстрирует рис.8.11. Блоки 1, 2, 3 и 4 реализуют функции двух переменных , ,, и соответственно. В блоке 5 и 6 исключается переменная x₂, а в блоке – x₁. Отметим, что полученная схема, начиная с яруса i и кончая последним ярусом, удовлетворяют условию каскадных схем.

Каскадной схемой называется схема, в которой выходной полюс элемента, попавшего в ярус с номером i, может быть непосредственно связан лишь с входными полюсами элементов, образующих ярус i+1.

Также, следует отметить, что остаточные функции могут быть одинаковы. Например, если

то == и ==.

В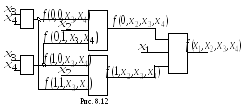ид схемы, реализующей такую функцию, иллюстрирует рис.8.12. То есть в общем случае в схеме, синтезированной методом каскадов, могут появиться ветвления.

Можно заметить, что задача синтеза оптимальных логических схем методом каскадов сводится к задаче построения бинарного графа с наименьшим числом вершин. Как было отмечено в гл.3.1, число вершин в бинарном графе зависит от порядка исключения переменных, а число всевозможных способов исключения растет комбинаторно. Поэтому, для выбора оптимального исключения переменных используют не простой перебор всех способов, а эвристические критерии. Рассмотрим один из таких критериев, основанный на использовании понятия производной от логической функции [2, с. 63-73].

Производная первого порядка от логической функции по переменной определяется следующим образом:

(8.1)

Пример 8.3. Вычислим производную от логической функции

.

Согласно определению,

.

Производная первого порядка от логической функции определяет условия, при которых эта функция изменяет значение на противоположное (переключается) при переключении переменной .

В примере 8.3 функция переключается при переключении , при условии, что конъюнкция принимает значение "истина", то есть . Восстановив таблицу истинности данной функции, легко увидеть, что при переключении c на , , функция также переключается c на .

Смешанной производной от логической функции называется выражение вида .

Смешанную производную k-го порядка вычисляют, применяя соотношение (8.1) k раз фиксацией переменных , ,..., (порядок фиксации переменных не имеет значения).

Производная k-го порядка от логической функции по переменным ,,...,определяет условия, при которых эта функция изменяет значение при одновременном изменении значений переменных ,,...,.

Согласно Бохману, производная k-го порядка от логической функции по переменным ,,..., равна сумме по модулю два всех производных первого порядка, вторых, третьих, ..., k-х смешанных производных при фиксации переменных ,,...,:

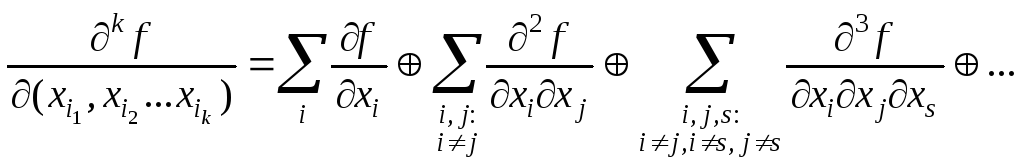
Пример 8.4. Определим условия переключения выходного канала логической схемы, реализующей функцию , при переключении каждого входного канала и первого и второго каналов одновременно и всех трех каналов одновременно. Имеем:

, ,

.

Условие является условием переключения выходного канала при переключении входного канала : при подаче на второй канал - 1 или на третий - 0, при переключении первого канала переключается выходной канал. Из условий и следует, что выходной канал переключается при переключении входного канала , если , и переключается, когда переключается , при , . Далее находим:

,

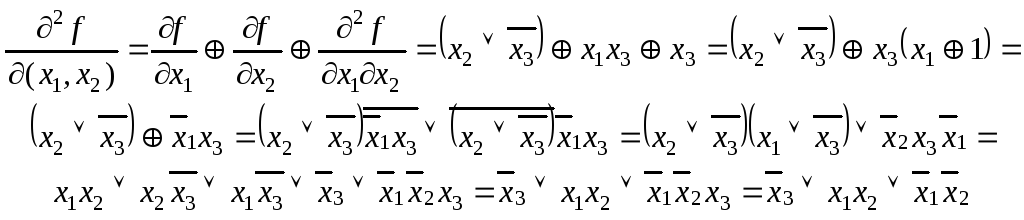
Выходной канал переключается при любом одновременном переключении входных каналов , когда , или независимо от состояния входного канала при переключении и с 1,1 на 0,0 или 0,0 на 1,1. Определим :

, ,

,

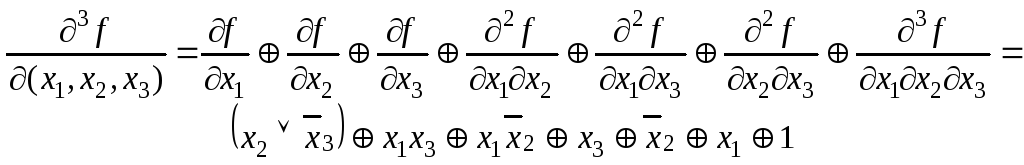
С помощью эквивалентных преобразований получим СДНФ производной 3-го порядка от (проделайте самостоятельно).

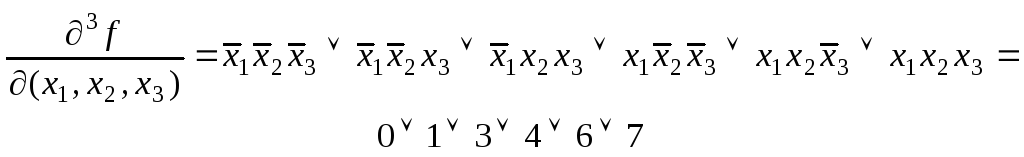
(конституенты единицы представлены своими десятичными номерами).

При переключении входного вектора ,, выходной канал переключается.

Критерий оптимального исключения переменных заключается в исключении сначала переменных, при переключении которых логическая функция переключается при максимальном числе условий. Это максимальное число определяется весом производной.

Весом производной от логической функции называется число конституент этой производной.

Если исключается k переменных, находят производные k-го порядка от данной функции и ищут максимальное значение веса производной

,

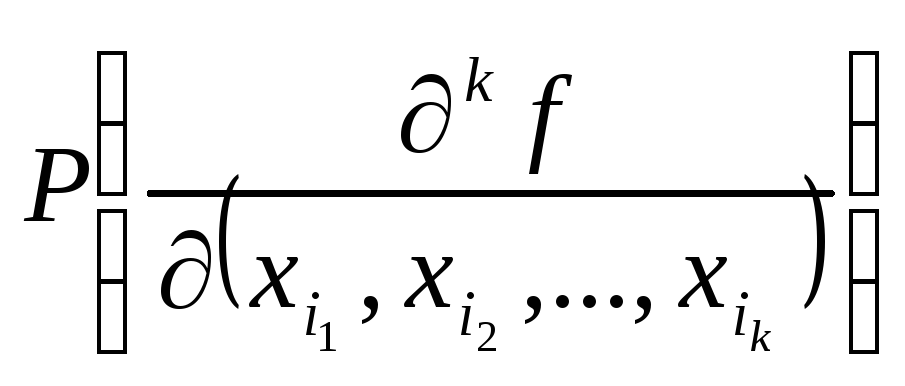которое и определяет исключаемые переменные.

Как было отмечено выше, данный критерий имеет эвристический характер, что основано на предположении о том, что чем больше вес производной , тем больше функция зависит от переменной .

Рассмотрим пример синтеза логической схемы методом каскадов.

Пример 8.5. Задана булева функция :

.

Требуется синтезировать логическую схему, реализующую данную функцию, используя блоки исключения одной переменной, двухвходовые логические элементы "И", "ИЛИ" и инверторы (рис. 8.13). Синтез схемы произвести методом каскадов. При выборе переменных исключения использовать эвристический критерий, основанный на весе производной (исключается переменная , по которой производная имеет максимальный вес).

Отметим, что вес производной логической функции не зависит от формы, в которой она представлена. Поэтому, при построении логической схемы методом каскадов с использованием критерия исключения переменных, основанного на весе производной, не обязательно минимизировать исходную логическую функцию, что существенно увеличит быстродействие при программной реализации метода.

Определим переменную , по которой производная имеет максимальный вес . Эта переменная и будет являться переменной исключения на первом ярусе логической схемы.

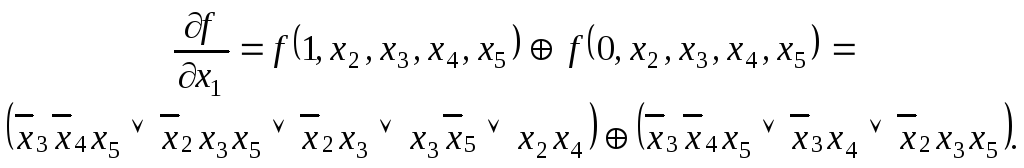
Таблица истинности функции приведена в табл. 8.1. Число наборов, на которых функция принимает единичное значение, равно 7, т.е. .

Аналогично найдем производные , , , :

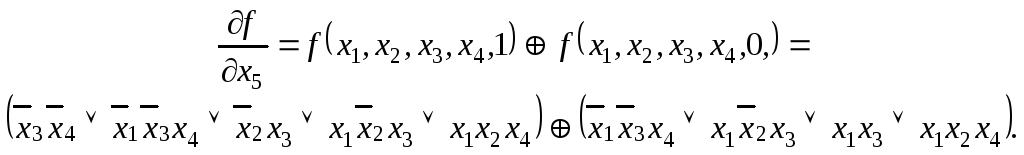
и их веса

Соответствующие таблицы истинности приведены в табл.8.2, 8.3, 8.4, 8.5. Максимальное значение веса производной получено для единственной переменной . Используя разложение Шеннона, исключим переменную из функции:

Здесь обозначено: и

, .

Таблица 8.1
x2x3	x4x5
	00	01	10	11
00	0	0	1	1
01	1	0	1	0
10	0	0	0	0
11	1	0	1	1

Таблица 8.2
x1x3	x4x5
	00	01	10	11
00	0	0	0	0
01	0	1	0	1
10	0	0	1	1
11	0	1	0	0

Таблица 8.3
x1x2	x4x5
	00	01	10	11
00	0	0	1	0
01	0	1	1	1
10	1	0	1	1
11	1	1	0	0

Таблица 8.4
x1x2	x3x5
	00	01	10	11
00	1	0	0	0
01	1	0	0	0
10	0	1	0	0
11	1	0	0	1

Аналогично определим оптимальное исключение переменных на следующем ярусе логической схемы, т.е., определим оптимальную переменную исключения для функции и . В общем случае, форма этих функций отлична от минимальной , но, как было сказано выше, вес производной логической функции не зависит от формы, в которой она представлена; следовательно, функции минимизировать не обязательно.

Таблица 8.5
x1x2	x3x4
	00	01	10	11
00	1	0	1	1
01	1	0	0	0
10	1	0	0	0
11	1	0	1	0

Опрeделим , , , ; соответствующие таблицы истинности приведены в табл. 8.6, 8.7, 8.8, 8.9.

, .

, .

, .

, .

Теперь определим , , , ; соответствующие таблицы истинности приведены в табл. 8.10, 8.11, 8.12, 8.13.

, .

, .

, .

, .

Таблица 8.6
x2	x4x5
	00	01	10	11
0	1	0	1	0
1	1	0	1	1
Таблица 8.8
x1	x2x5
	00	01	10	11
0	0	0	0	0
1	0	0	0	1
Таблица 8.10
x2	x4x5
	00	01	10	11
0	0	0	1	1
1	0	0	0	0
Таблица 8.12
x1	x2x5
	00	01	10	11
0	1	0	1	0
1	0	1	1	0

Таблица 8.7
x1	x4x5
	00	01	10	11
0	0	1	0	1
1	0	1	0	0
Таблица 8.9
x1	x2x4
	00	01	10	11
0	1	1	0	0
1	0	0	1	0
Таблица 8.11
x1	x4x5
	00	01	10	11
0	0	0	0	0
1	0	0	1	1
Таблица 8.13
x1	x2x4
	00	01	10	11
0	1	0	1	0
1	1	0	1	0

Итак, в по данному критерию мы могли исключить только одну переменную x₃ (см. выше). В также исключается одна переменная x₁. При этом получаются следующие остаточные функции:

Здесь обозначено: и

,

Следует отметить, что больше переменные исключаться не будут. Т.е., мы считаем, что остаточные функции от трех переменных достаточно простые и подлежат реализации на имеющихся двухвходовых логических элементах (см. рис. 8.13), поэтому, они все должны быть минимизированы (функция существенно упростилась, см. выше).

В можно исключить две переменные x₄ или x₅ , т.к. . Исследуем оба случая.

Исключая x₄, получаем остаточные функции

Здесь обозначено: и

,

Исключая , получаем

Здесь обозначено: и ,

,

.

Эти результаты иллюстрируют бинарные графы на рис.8.14 и 8.15.

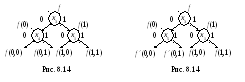
Таким образом, при использовании критерия исключения переменных, основанного на весе производной, можно получить две схемы (рис 8.16, 8.17).

Итак, мы синтезировали схемы, реализующие булеву функцию от пяти переменных. Синтез схем производился методом каскадов с использованием критерия, основанного на весе производной булевой функции. В результате получились две схемы, содержащие 19 и 23 логических элементов, реализующих дизъюнкцию, конъюнкцию и отрицание (блок исключения одной переменной состоит из четырех указанных элементов).

Заметим, что в примере 8.2, для той же функции была синтезирована схема путем непосредственного моделирования. Такая схема содержала 18 аналогичных логических элементов. Т.о., при использовании метода каскадов и метода непосредственного моделирования, в данном случае были синтезированы примерно одинаковые по сложности (числу элементов) схемы. Однако, как было отмечено выше, при синтезе схемы методом каскадов функция может быть представлена в любой форме. При построении схемы путем непосредственного моделирования, в качестве исходной формы функции использовалась выходная форма факторного алгоритма. Получение минимальной (или даже тупиковой) формы функции, а затем выполнение факторизации является довольно трудоемким процессом. Поэтому, при программной реализации метод каскадов может оказаться более предпочтительным.