гл4

Найти методом Блейка-Порецкого сокращенную ДНФ функции .

Проводим обобщенные склеивания. Легко видеть, что первая и вторая конъюнкции допускают обобщенное склеивание по переменной. В результате склеивания имеем:

Первая и третья конъюнкции исходной ДНФ допускают обобщенное склеивание, как по переменной ,так и по . После склеивания по имеем:

После склеивания по имеем:

Вторая и третья конъюнкции ДНФ допускают обобщенное склеивание по переменной . После склеивания получаем:

Выполнив последнее обобщенное склеивание, приходим к ДНФ

.

После выполнения поглощений получаем

Попытки дальнейшего применения операции обобщенного склеивания и поглощения не дают результата. Следовательно, получена сокращенная ДНФ функции . Далее задача поиска минимальной ДНФ решается с помощью импликантной матрицы точно также как в методе Квайна.

4.3. Минимизация частичных функций

На случай частичных функций, понятие простого импликанта обобщается следующим образом. Конъюнкция K называется простым импликантом частичной функции f, если:

• она покрывает хотя бы один набор 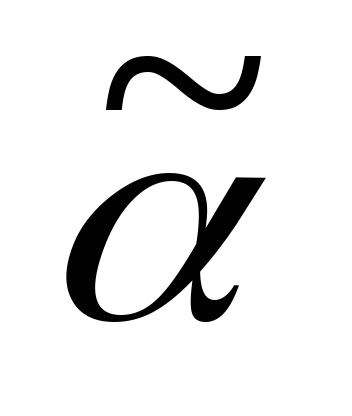, на котором ;

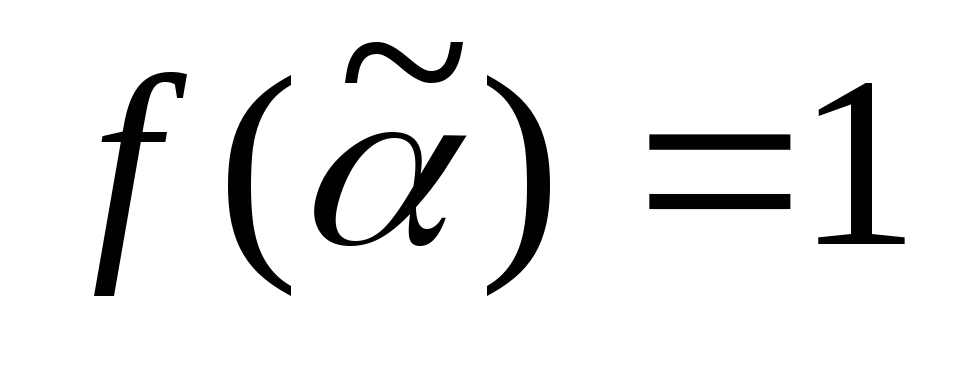• не покрывает ни одного набора 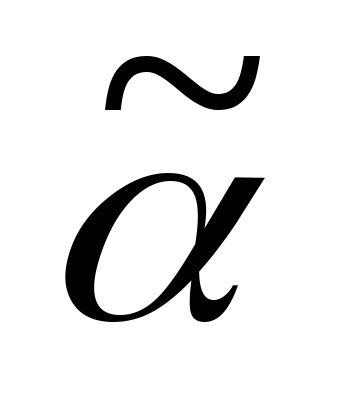, такого что ;

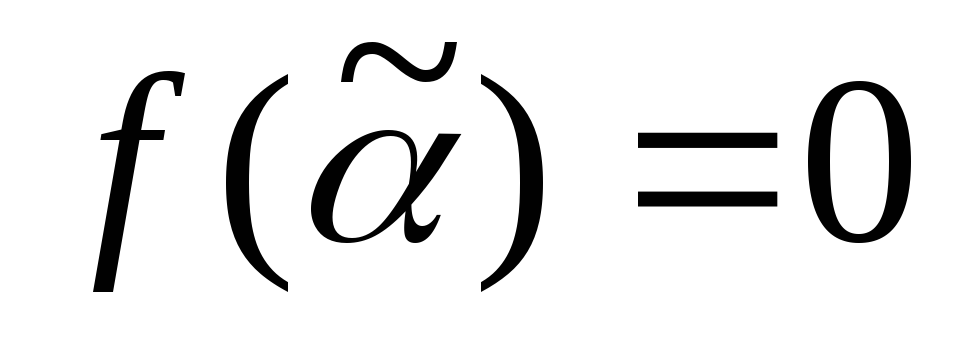• любая конъюнкция, полученная из нее вычеркиванием переменных, покрывает некоторый набор на котором .

Алгоритм поиска МДНФ частичной функции может быть следующий.

1. Доопределить единицами исходную функцию 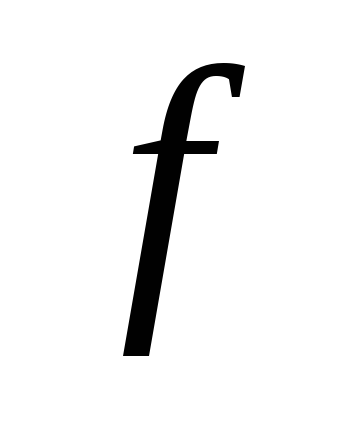на всех неопределенных наборах и получить все простые импликанты (сокращенную ДНФ), например, так как это было сделано в методе Квайна (гл. 4.1). Доопределение частичной функции 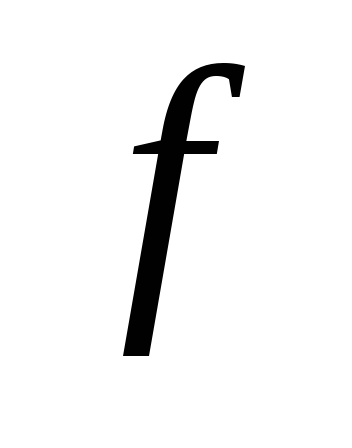единицами гарантирует, что будут получены все возможные простые импликанты .

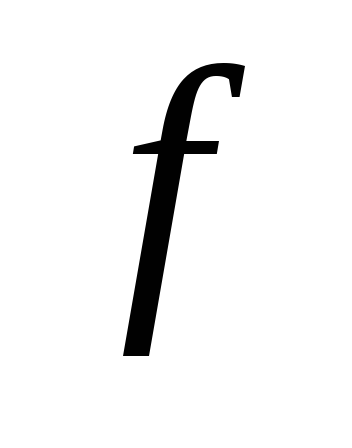2. Получить МДНФ по импликантной матрице, где в столбцах выписаны лишь те конституенты единицы функции 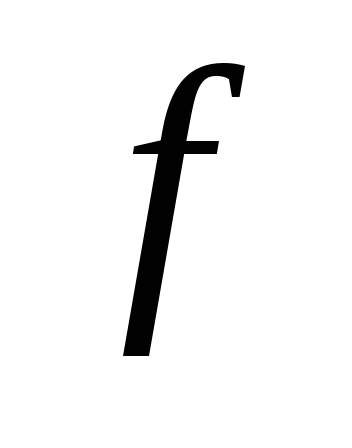, которые соответствуют полностью определенным единичным наборам.

Можно предложить и другую организацию поиска системы всех простых импликантов. Рассмотрим такую организацию на примере частичной логической функции , заданной табл. 4.4. Для удобства представим эту функцию в виде таблиц и , в первой из которых перечислены единичные наборы функции , а во второй - нулевые. Таблицы и представлены табл. 4.5 и 4.6 соответственно.

Таблица 4.6

0 0 0 1 1 0 0 0 1 1 0 0 1 1 1 0

Таблциа 4.5

0 1 0 0 0 1 1 0 1 0 1 0 1 1 1 1

Таблица 4.4
0 0 0 1 0 1 0 0 0 1 1 0 1 0 0 0 1 0 1 0 1 1 0 0 1 1 1 0 1 1 1 1	0 1 1 0 1 0 0 1

Метод построения всех простых импликантов для частичной функции проиллюстрирован в табл. 4.7. В колонке 1 помещены все наборы таблицы . В колонке 2 содержатся всевозможные наборы, образованные из наборов колонки 1 вычеркиванием одного разряда и обладающие тем свойством, что они не покрывают (не совпадают с ними в невычеркнутых разрядах) никаких наборов таблицы . Они могут быть найдены просмотром всех наборов колонки 1 и проверкой возможности вычеркивания в каждом из них каждого из символов. Наборы колонки 1, покрываемые наборами колонки 2, помечаются значком . В колонке 3 находятся все наборы, полученные из наборов колонки 2 заменой одного разряда прочерком и не покрывающие наборов таблицы . Покрытые ими наборы колонки 2 помечаются значком . Из наборов колонки 3 уже не удается образовать наборов с тремя прочерками, не покрывающих наборов из таблицы . На этом процедура заканчивается, все непомеченные наборы табл. 4.7 соответствуют простым импликантам. В данном случае это , , , , ,

Таблица 4.7
1	2	3
0100 0110 1010 1111	0-00 01-0 010- 0-10 011- -010 101- -111 1-11 11-1	0--0 01-- 0-1- -01- --11 -1-1 1--1

Далее, как и в случае всюду определенных функций, строится импликантная матрица и ищется ее покрытие. Для рассматриваемой функции импликантная матрица приведена в табл. 4.8. Видно, что данная матрица имеет несколько минимальных покрытий, соответствующих МДНФ функции. Примером МДНФ может служить

Таблица 4.8
	0100	0110	1010	1111
	*	*
	*	*
		*
			*
				*
				*
				*

Задания для самостоятельной работы

4.1. Доказать, что дизъюнкция любого числа импликант логической функции также является импликантом этой функции.

Указание. При доказательстве можно воспользоваться определением импликанта и законом дистрибутивности конъюнкции относительно дизъюнкции (2.3).

4.2. Написать подпрограмму, производящую склеивание двух элементарных конъюнкций и , заданных своими векторами вхождения и обращения, каждый из которых занимает одно машинное слово (т. е. число переменных в конъюнкциях меньше, чем разрядность машины). Результат склеивания также оформить в виде вектора вхождения и обращения. Если и не склеиваются, то выдавать два нулевых слова.

4.3. Используя результаты задачи 4.2, программно реализовать минимизацию булевых функций методом Квайна. Исходная логическая функция задается вектором значений.

Указание. При реализации этапа получения сокращенной ДНФ используйте разбивку конъюнкций на пояса (см. выше). При разработке алгоритма решения поставленной задачи воспользуйтесь идеей быстрого подсчета единичных разрядов в машинном слове, которая разбиралась в задаче 1.10.

4.4. Разработать структуру хранения бинарного графа и реализовать алгоритм его построения (рис.3.2), если исходная булева функция задана в ДНФ, каждая элементарная конъюнкция представлена векторами вхождения и обращения. Выбор переменной разложения в алгоритме построения бинарного графа осуществлять произвольно.

4.5. Из заданного множества элементарных конъюнкций K выделить простые импликанты , если:

1) , ;

2) , ;

3) , .

4.6. С помощью метода Блейка-Порецкого построить сокращенную ДНФ по заданной ДНФ D.

;

;

.

4.7. Сокращенную ДНФ функции , заданной в виде КНФ, можно получить следующим образом. Сначала раскрыть скобки, пользуясь законом дистрибутивности, затем вычеркнуть из получившейся ДНФ буквы и конъюнкции, используя правила , , , . Например, функция задана КНФ . Раскрыв скобки, получим ДНФ функции . Применяя указанные выше правила, получим функцию в сокращенной ДНФ: .

Получить сокращенную ДНФ функции f заданной КНФ:

;

;

.

4.8. Построить все тупиковые ДНФ следующих функций:

;

;

.

4.9. Выяснить, являются ли тупиковыми или минимальными следующие ДНФ:

;

;

.

4.10. Переменная является существенной переменной функции тогда, и только тогда, когда эта переменная явно входит в сокращенную ДНФ функции . Получить сокращенную ДНФ функции и указать существенные переменные.

;

;

.

1⁾ Условные графические обозначения элементов, реализующих элементарные функции и правила изображения элементов, реализующих более сложные логические функции, регламентируются ГОСТом 2.743-72 и приведены в приложении 1 настоящего руководства.