§3. Умножение вероятностей независимых событий.
Введение (о независимых событиях)
Событие
В
н
е з а в и с и т от события А , если
,
т.е. вероятность события В не зависит
от того, произошло ли событие А.В
этом случае и событие А не зависит от
события В, т.е.
- свойство независимости событий является
взаимным.
|
|
Условие |
А |
В |
Р(В)
|
Вывод о зависимости А и В | |
|
|
| |||||
|
1 |
В ящике 5 деталей, среди которых 3 стандартные и 2 бракованные. Поочередно извлекают по одной детали, не возвращая их назад. Какова вероятность извлечения во второй раз стандартной детали? |
Извлечена стандартная деталь в 1 раз |
Извлечена стандартная деталь во 2 раз |
|
|
Зависимы |
|
2 |
В ящике 5 деталей, среди которых 3 стандартные и 2 бракованные. Поочередно извлекают по одной детали, возвращая их назад. Какова вероятность извлечения во второй раз стандартной детали? |
Извлечена стандартная деталь в 1 раз |
Извлечена стандартная деталь во 2 раз |
|
|
Независимы |
С
войство
независимости событий взаимно, т.е.
если событие В не зависит от события А,
то и событие А не зависит от события В.
Н
есколько
событий А, В,……К
называются
независимыми
в совокупности, если независимы любые
два из них и независимы любое из данных
событий и любые комбинации (произведения)
остальных событий.
Например, три события А, В, С независимы в совокупности, если независимы события А и В, А и С, В и С, А и ВС, В и АС, С и АВ.
Вероятность
произведения
двух или нескольких независимых событий
равна произведению вероятностей этих
событий: Р(А·В) = Р(А)·Р(В)
|
|
Условие |
А |
Р(А) |
В |
Р(В)
|
Р(АВ)
|
|
1 |
Подбрасываются 2 монеты. Какова вероятность того, что появятся 2 цифры? |
Цифра на 1 монете |
|
Цифра на 2 монете |
|
|
|
2 |
Два стрелка попадают в мишень соответственно с вероятностью 0,8 и 0,7. Какова вероятность того, что при одном выстреле оба попадут в мишень? |
|
|
|
|
|
|
3 |
В каждом из двух ящиков находится по 30 деталей. В первом ящике 27 стандартных, а во втором – 28. Из каждого ящика наудачу вынимают по одной детали. Какова вероятность того, что обе детали окажутся стандартными? |
|
|
|
|
|
§4. Теоремы о вероятности совместных событий.
В
ероятность
суммы
двух совместных событий ( т.е. вероятность
появления хотя бы одного) равна сумме
вероятностей этих событий без вероятности
их произведения:
Р(А+В )= Р(А)+Р(В) – Р(АВ)
|
|
Условие |
А |
Р(А) |
В |
Р(В) |
А·В |
Р(АВ) |
Р(А+В)
|
|
1 |
Два стрелка попадают в мишень соответственно с вероятностью 0,85 и 0,8. Стрелки независимо сделали по одному выстрелу. Какова вероятность того, что хотя бы один попадет в мишень? |
Первый попал |
|
Второй попал |
|
Оба попали |
|
|
|
2 |
Наудачу взято двузначное число. Какова вероятность того, что это число окажется кратным 2 или 7 или тому и другому одновременно? |
|
|
|
|
|
|
|
|
3 |
На 30 жетонах написаны 30 двузначных чисел от 1 до 30. Наудачу взят жетон. Какова вероятность того, что это число окажется кратным 2 или 3? |
|
|
|
|
|
|
|
|
4 |
Найти вероятность того, что при подбрасывании игрального кубика на верхней грани окажется четное или кратное трем число очков. |
|
|
|
|
|
|
|
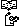
В
ероятность
суммы
нескольких совместных событий равна
разности между единицей и вероятностью
произведения противоположных событий:
Р(А+В+….+К)
=1
-
Р(
·
·
…..·
)
|
|
Условие |
А |
|
В |
|
С |
|
Р(А+В+С) |
|
1 |
Вероятность попадания в цель при стрельбе из трех орудий таковы: 0,75; 0,8; 0,85. Какова вероятность хотя бы одного попадания при одном залпе из всех орудий? |
Попадание 1 орудия |
|
Попадание 2 орудия |
|
Попадание 3 орудия |
|
|
|
2 |
На 100 лотерейных билета приходится 5 выигрышных. Какова вероятность выигрыша хотя бы по одному из 3 купленных билетов? |
|
|
|
|
|
|
|
|
3 |
Вероятность того, что студент сдаст первый экзамен, равна 0,9; второй – 0,9; третий- 0,8. Какова вероятность того, что студент сдаст хотя бы один экзамен? |
|
|
|
|
|
|
|
|
|
Условие |
|
… |
|
Р( |
… |
Р( |
n |
|
1 |
Сколько раз нужно подбросить два игральных кубика, чтобы вероятность выпадения хотя бы один раз двух шестерок была бы больше 1/2? |
Выпадение 6 при 1 подбрасывании |
|
Выпадение 6 при i подбрасывании |
|
|
|
25
|
|
2 |
Вероятность попадания в десятку при одном выстреле стрелка равна 0,6. Сколько выстрелов должен сделать стрелок, чтобы с вероятностью не менее 0,8 он попал в десятку хотя бы один раз? |
|
|
|
|
|
|
2 |
)
)
