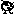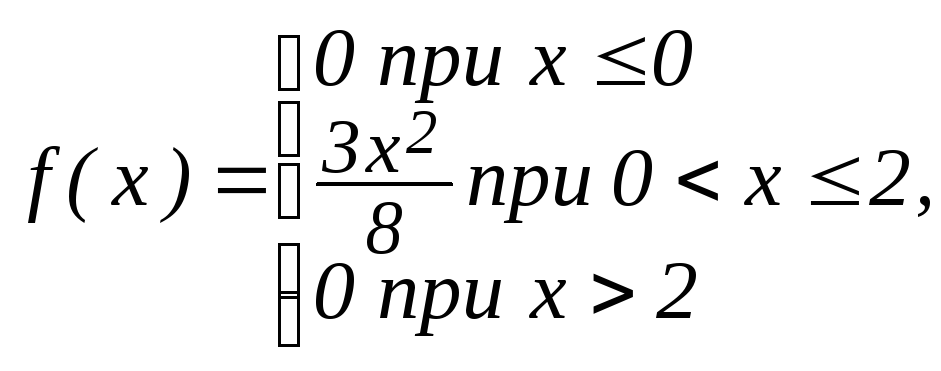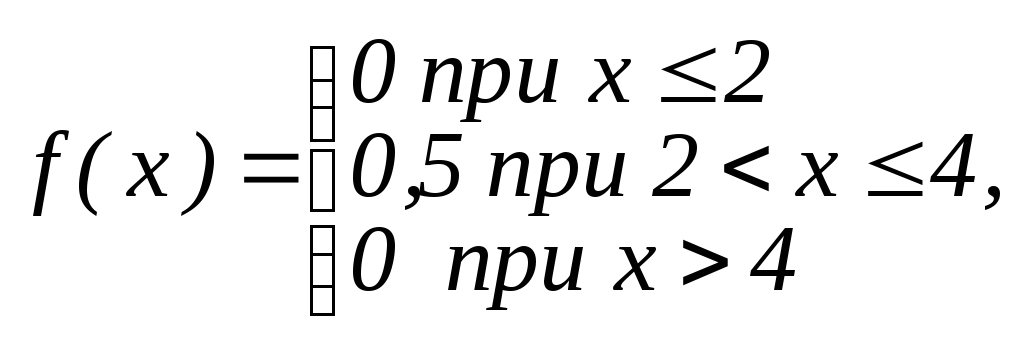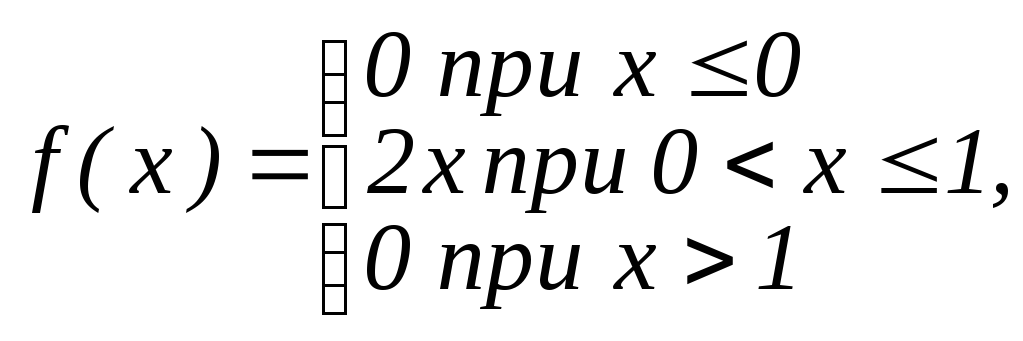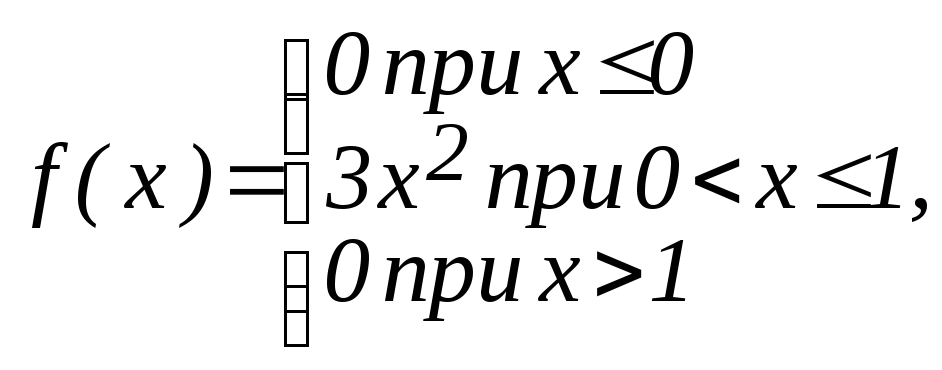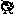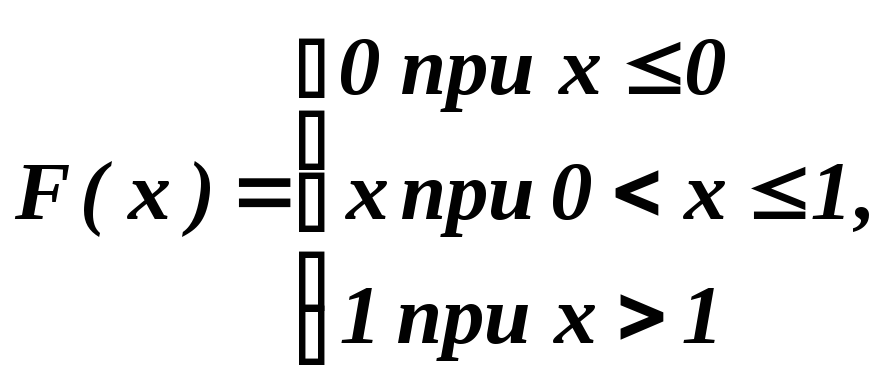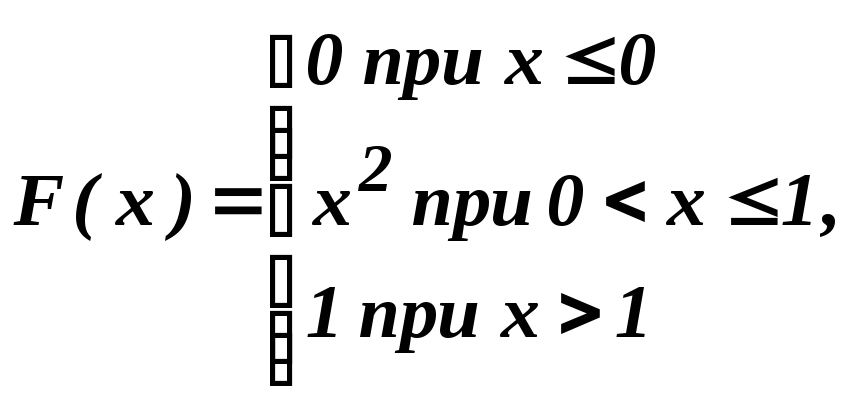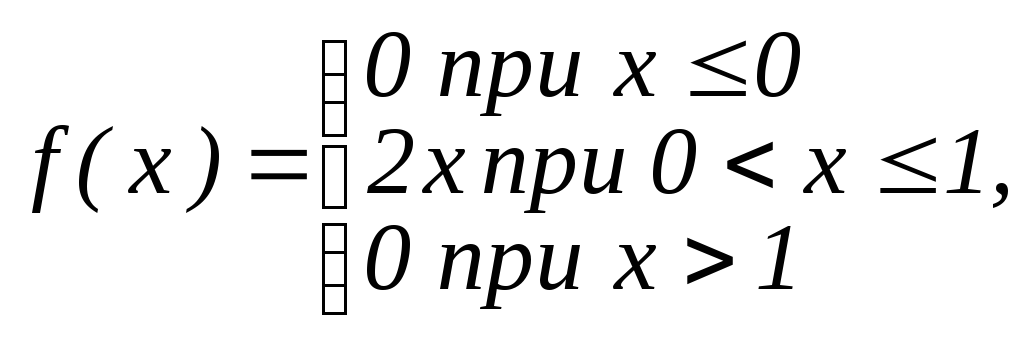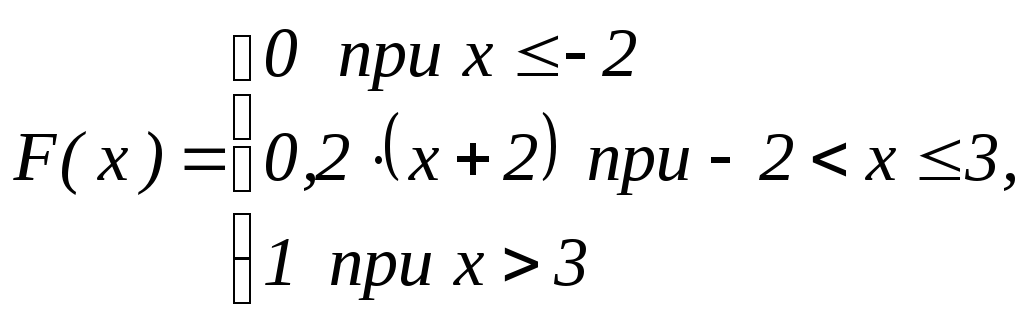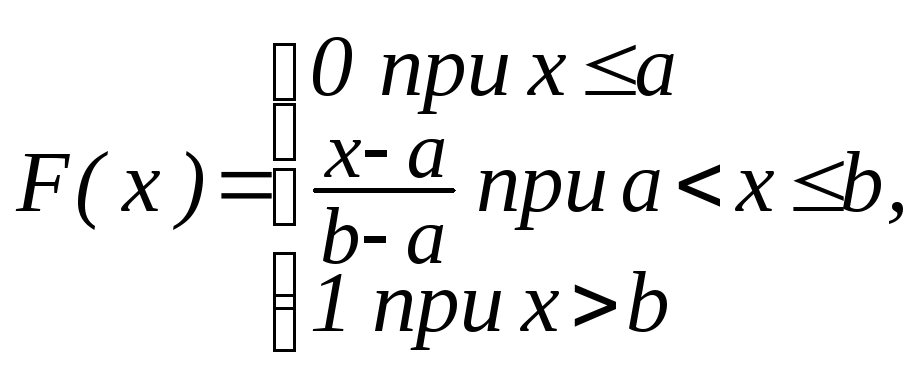§3. Числовые характеристики непрерывных случайных величин

Пусть непрерывная случайная величина Х задана плотностью распределения f(x) и все возможные значения Х принадлежат отрезку [a, b]. Разобьем этот отрезок на n частичных отрезков длиной и в каждом из них выберем произвольную точку. Напомним, чтоприближенно равно вероятности попаданияХ в интервал , поэтому по аналогии с математическим ожиданием дискретной случайной величины составим сумму произведений значенийна вероятности попадания их в интервал:. Перейдем к пределу при стремлении к нулю длины наибольшего из частичных отрезков, получим определенный интеграл, который и называют математическим ожиданием непрерывной случайной величины.

Математическим ожиданием непрерывной случайной величины Х, возможные значения которой принадлежат отрезку [a, b], называют определенный интеграл

M(X) =

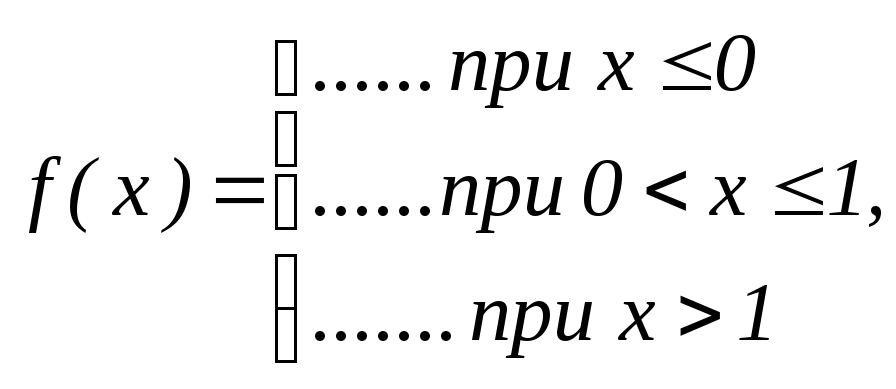
Найти математическое ожидание случайной величины Х, заданной плотностью распределения f(x):

№	Плотность распределения f(x)	Математическое ожидание M(X)
1		M(X) = 1,5
2
3
4

Найти математическое ожидание случайной величины Х, заданной функцией распределения F(x):

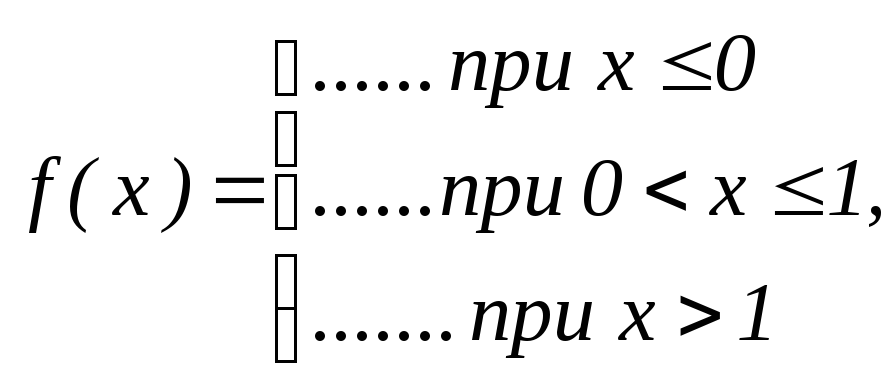
№	Функция распределения F(x)	Плотность распределения f(x)=	Математическое ожидание M(X)
1			M(X) = 0,5
2

Дисперсией непрерывной случайной величины Х, возможные значения которой принадлежат отрезку [a, b], называют математическое ожидание квадрата ее отклонения: D(X) =

Средним квадратическим отклонением непрерывной случайной величины Х, называют корень квадратный из ее дисперсии:

Найти дисперсию и среднее квадратическое отклонение случайной величины Х, заданной плотностью распределения f(x).

№	f(x)	M(X)	D(X)
1				0,24
2
3

Легко получить еще одну формулу для вычисления дисперсии: D(X) =

Найти дисперсию и среднее квадратическое отклонение случайной величины Х, заданной функцией распределения F(x):

	1	2
F(x)
f(x)
M(X)
D(X)

50