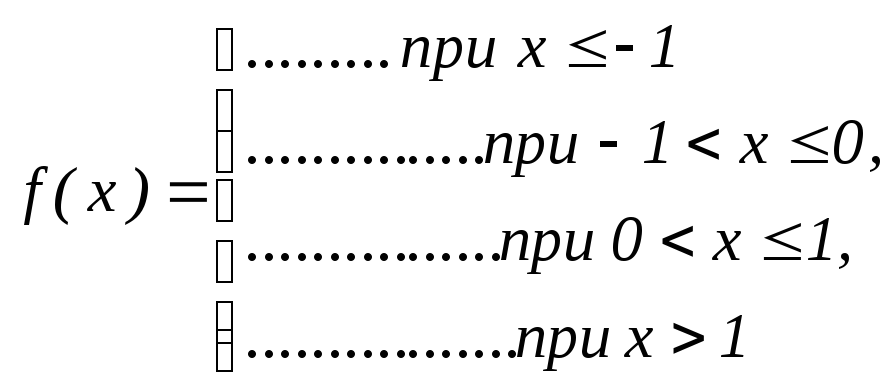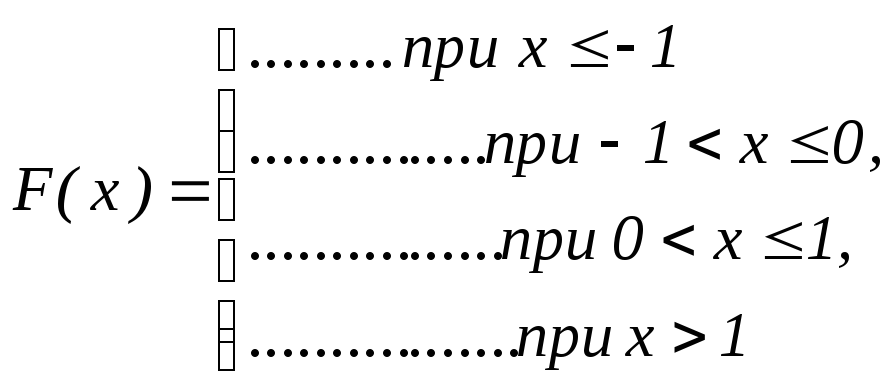§2 Плотность вероятности непрерывной случайной величины
п.1. Определение.
П
 лотностью
вероятности
( плотностью распределения или плотностью
или дифференциальной функцией) f(x)
непрерывной случайной величины Х
называется производная ее функции
распределения:
лотностью
вероятности
( плотностью распределения или плотностью
или дифференциальной функцией) f(x)
непрерывной случайной величины Х
называется производная ее функции
распределения:
![]() .
.
Найти плотность вероятности случайной величины Х:
|
№ |
Функция распределения F(x) |
Плотность вероятности f(x) |
|
1 |
|
|
|
2 |
|
|
|
3 |
|
|
п .2.
Cвойства плотности
вероятности
.2.
Cвойства плотности
вероятности
Плотность вероятности – неотрицательная функция:
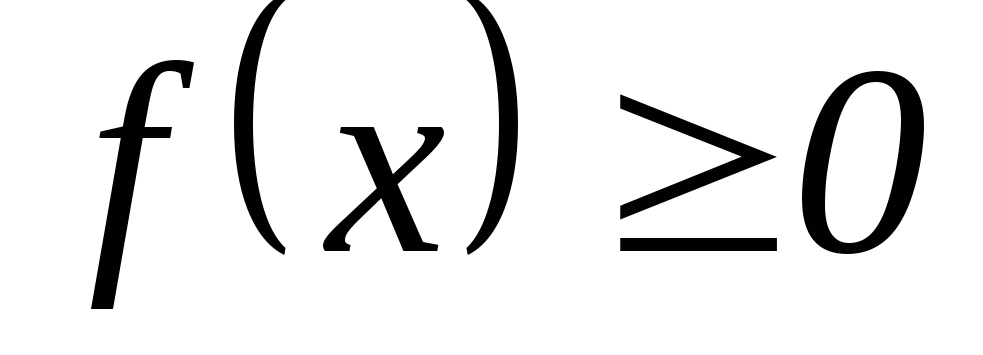 .
.
Доказательство очевидно, т.к. функция F(x) - неубывающая.
 2.
Вероятность попадания непрерывной
случайной величины в интервал (а,
в)
равна определенному интегралу от
плотности распределения, взятому в
пределах от а
до в:
2.
Вероятность попадания непрерывной
случайной величины в интервал (а,
в)
равна определенному интегралу от
плотности распределения, взятому в
пределах от а
до в:
![]()

![]()
П лотность
вероятности случайной величины Х задана
функциейf(x).
Найти вероятность того, что в результате
испытания величина примет значение из
данного интервала.
лотность
вероятности случайной величины Х задана
функциейf(x).
Найти вероятность того, что в результате
испытания величина примет значение из
данного интервала.
|
№ |
Плотность вероятности f(x) |
(а, b) |
|
Р |
|
1 |
|
(1, 2) |
|
|
|
2 |
|
(0,5;1) |
|
|
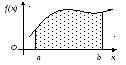
 Вероятность
попадания непрерывной случайной величины
в интервал (а,
b)
равна площади криволинейной трапеции,
ограниченной осью абсцисс, кривой
распределения f(x)
и прямыми
Вероятность
попадания непрерывной случайной величины
в интервал (а,
b)
равна площади криволинейной трапеции,
ограниченной осью абсцисс, кривой
распределения f(x)
и прямыми
х = а и х = b.
Н айти
плотность вероятности случайной величиныХ,
заданной функцией распределения F(x).
Построить графики функций. Найти
вероятности Р(x
< 1),
айти
плотность вероятности случайной величиныХ,
заданной функцией распределения F(x).
Построить графики функций. Найти
вероятности Р(x
< 1),
![]() ,
показать
вероятности
на
графиках.
,
показать
вероятности
на
графиках.
|
Функция распределения F(x) |
Плотность вероятности f(x) |
|
|
|
|
|
х |
|
F(1) – ордината графика |
Площадь под кривой распределения на [0,1] |
|
F(2) - F(1) – приращение ординаты на отрезке [1,2] |
Площадь под кривой распределения на [1,2] |
Н айти
плотность вероятности случайной величиныХ,
заданной функцией распределения F(x).
Построить графики функций. Найти
вероятность
айти
плотность вероятности случайной величиныХ,
заданной функцией распределения F(x).
Построить графики функций. Найти
вероятность![]() ,
показать вероятности на графиках.
,
показать вероятности на графиках.
|
Функция распределения F(x) |
Плотность вероятности f(x) |
|
|
|
|
|
|
|
|
|

п.3. Нахождение функции распределения по известной плотности вероятности.
П усть
дана плотность распределенияf(x),
найдем функцию распределения F(x).
По определению F(х)
= Р(Х
< х)
=
усть
дана плотность распределенияf(x),
найдем функцию распределения F(x).
По определению F(х)
= Р(Х
< х)
=
![]() =
=![]() .
Итак,
F(х)
=
.
Итак,
F(х)
=![]()

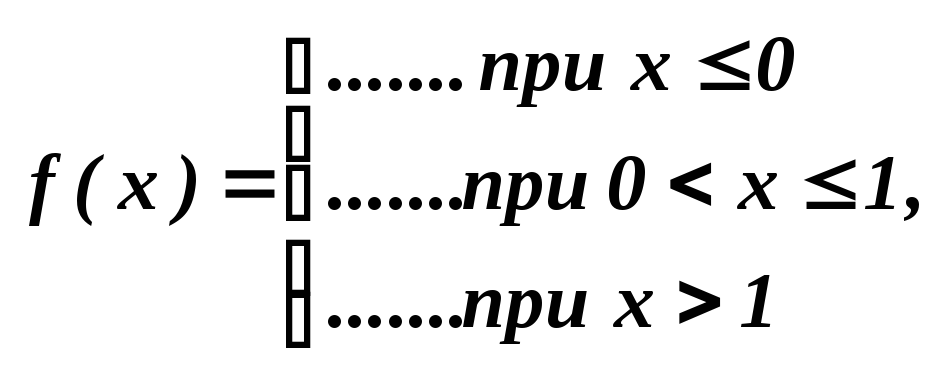
По данной плотности распределения найти функцию распределения:
|
f(x) |
F(x) | ||
|
|
| ||
|
|
….. |
….. | |
|
|
….. |
……. |
F(х)=
|
|
|
….. |
….. |
F(х)= +
|

По данной плотности распределения найти функцию распределения.
|
f(x) |
F(x) | |
|
|
| |
|
|
…. |
…. |
|
|
…. |
F(х)=………
|
|
|
…. |
F(х)=………
|
|
|
…. |
F(х)=………
|
 По
графику плотности распределения найти
функцию распределения и построить ее
график
По
графику плотности распределения найти
функцию распределения и построить ее
график
|
f(x) |
F |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
п .4.
Вероятностный смысл плотности
распределения
.4.
Вероятностный смысл плотности
распределения
Пусть
F(x)
–
функция распределения непрерывной
случайной величины X. По определению
плотности распределения f(x)
=
![]() =
=![]()
![]()
Как
известно, разность
![]() - вероятность того, что Х примет значение
из интервала
- вероятность того, что Х примет значение
из интервала![]() .
Таким образом,предел
отношения вероятности того, что
непрерывная случайная величина примет
значение из интервала
.
Таким образом,предел
отношения вероятности того, что
непрерывная случайная величина примет
значение из интервала
![]() ,
к длине этого интервала ( при
,
к длине этого интервала ( при![]() )
равен значению плотности распределения
в точке х.
)
равен значению плотности распределения
в точке х.
Далее,
![]() ,
т.е.
,
т.е.![]() .
.
 Вероятность
того, что случайная величина примет
значение из интервала
Вероятность
того, что случайная величина примет
значение из интервала
![]() приближенно равна произведению плотности
вероятности в точке на длину интервала
приближенно равна произведению плотности
вероятности в точке на длину интервала![]() .
.

Геометрически:
вероятность того, что случайная величина
примет значение из интервала
![]() приближенно равна площади прямоугольника
с основанием
приближенно равна площади прямоугольника
с основанием
![]() и
высотой f(х).
Истинная вероятность, определяемая
определенным интегралом
и
высотой f(х).
Истинная вероятность, определяемая
определенным интегралом
![]() ,
равна площади криволинейной трапеции.
Допущенная погрешность равна площади
криволинейного треугольника АВС.
,
равна площади криволинейной трапеции.
Допущенная погрешность равна площади
криволинейного треугольника АВС.


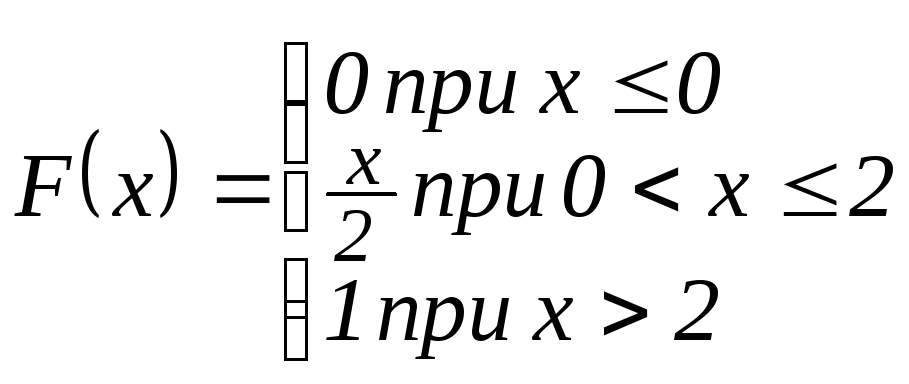
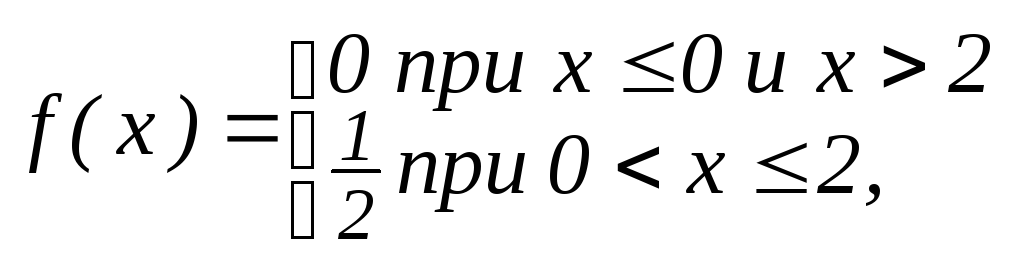

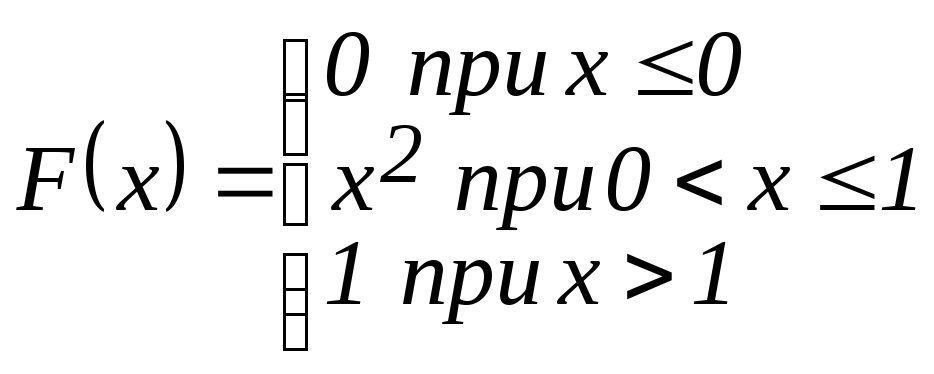



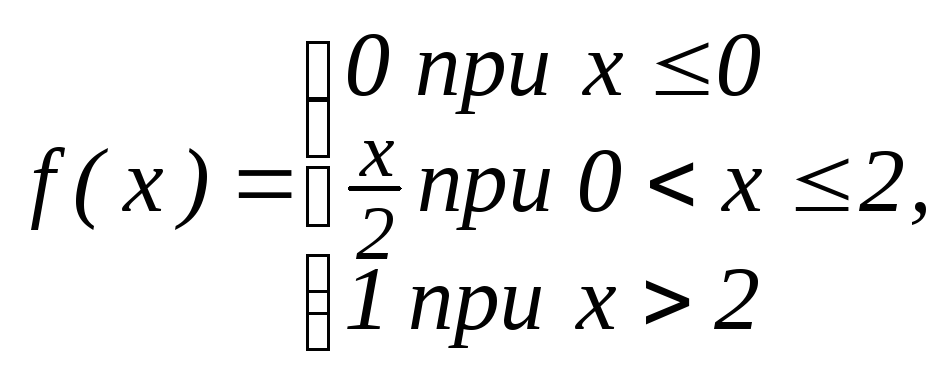



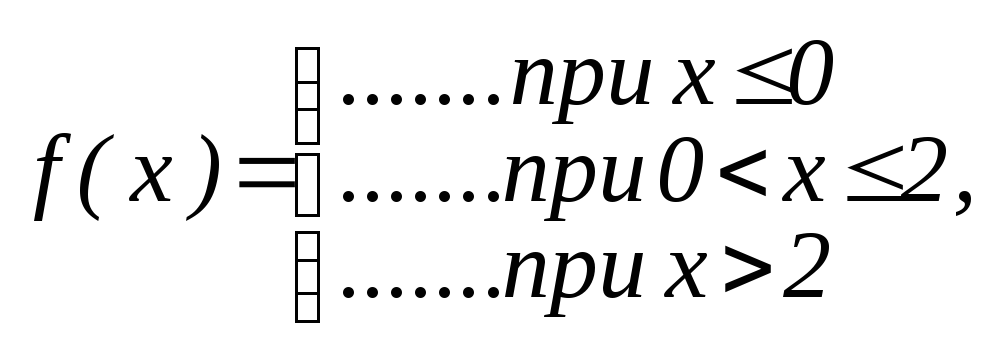



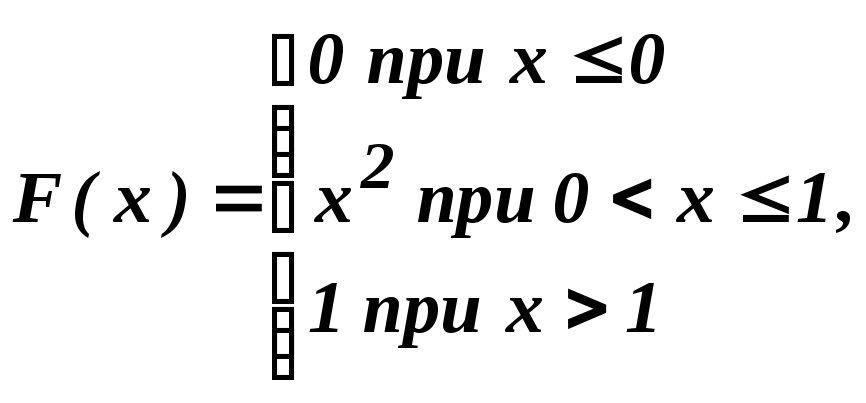


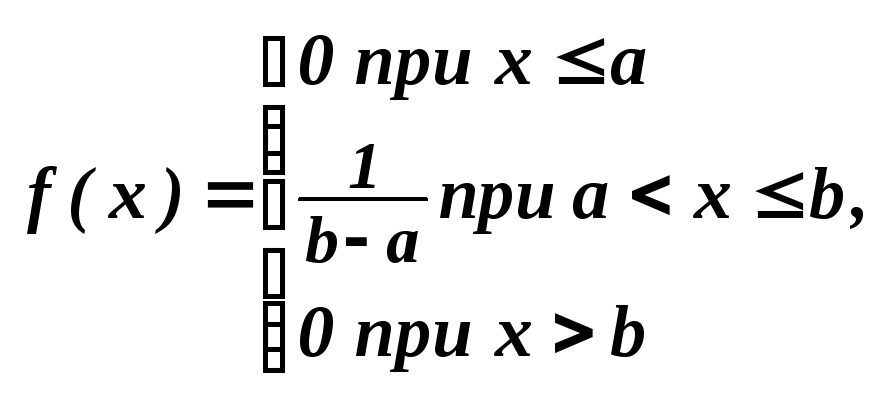
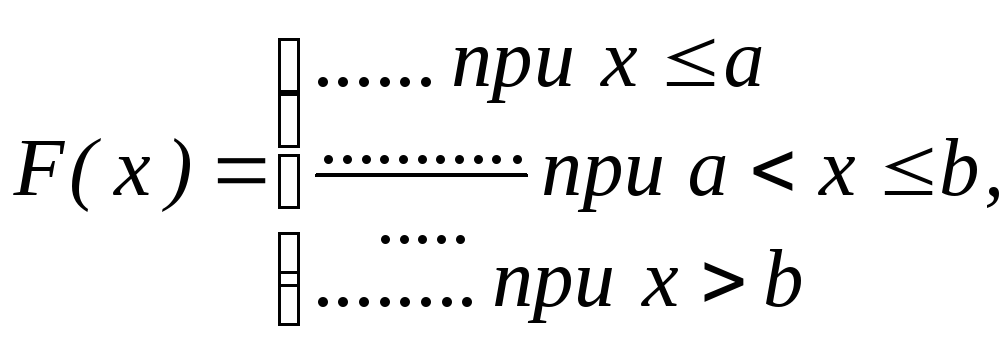

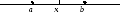







 (x)
(x)