
динамика
.pdf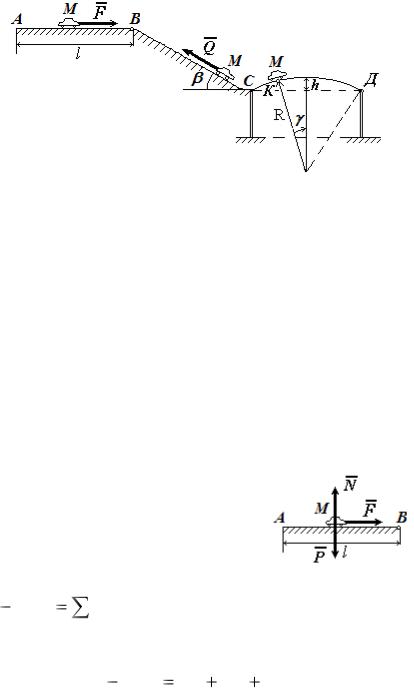
V. Примеры выполнения задач Пример решения задачи Д1
Автомобиль М массой m = 1 т, имея в точке А начальную скорость V0 = 15 м/с, движется по трассе АВС и по мосту СД (рисунок 22); участок трассы АВ горизонтальный, имеет длину l = 20 м, а участок ВС составляет угол β = 80 с
горизонтом. На участке трассы АВ действует постоянная сила |
F = 2 кН. На |
участке трассы ВC на автомобиль действует постоянная |
сила трения |
|
|
Fтр (значение коэффициента трения скольжения f = 0,05). В точках В и С
автомобиль не изменяет модуля своей скорости. Мост образует дугу окружности радиуса R = 50 м. Максимальная выпуклость моста h = 8 м.
Рисунок 22 – Движение автомобиля по трассе и мосту
Считая автомобиль материальной точкой, определить:
1.скорости автомобиля в точках В, С трассы и в точке К моста, если заданы:
-время движения t2 = 5 сек по участку ВС,
-угол, определяющий положение точки К, γ = 150;
2.силу давления автомобиля на мост, когда он находится в точке К, и установить, находится или нет автомобиль в точке К в отрыве от моста.
Решение.
1. Найдем скорость автомобиля в точке В (рисунок 23).
Так как задана длина участка, целесообразно применить теорему об изменении кинетической энергии точки в конечной форме, принимая за начальную точку А, а за конечную – точку В
m V 2 |
|
m V 2 |
Рисунок 23 – Движение по участку АВ |
|
В |
|
А |
Аk |
|
2 |
2 |
|||
|
||||
или применительно к данной задаче
m V 2 |
|
m V 2 |
|
|
|
|
В |
|
А |
AP |
AN |
АF , |
|
2 |
2 |
|||||
|
|
|
||||
где АР - работа силы тяжести на перемещении АВ, АN – работа нормальной
71
|
|
|
|
|
|
|
|
|
|
|
|
|
реакции на том же перемещении, АF – работа силы F. |
||||||||||||
Вычислим работы сил: |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||
АР =АN = 0, так как силы Р |
и |
N перпендикулярны к направлению перемещения. |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
АF = F · l, так как сила F совпадает с направлением перемещения. |
||||||||||||
По теореме об изменении кинетической энергии точки |
||||||||||||
|
|
|
|
m V2 |
|
m V2 |
|
|
|
|
||
|
|
|
|
В |
|
|
|
А |
|
F |
l . |
|
|
|
|
2 |
|
|
|
2 |
|
||||
|
|
|
|
|
|
|
|
|
|
|||
Из этого выражения получим |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|||
|
V 2 |
|
|
|
|
|
|
|
||||
V |
2 |
F l / m |
|
225 |
80 17,46 м/с. |
|||||||
В |
A |
|
|
|
|
|
|
|
|
|
|
|
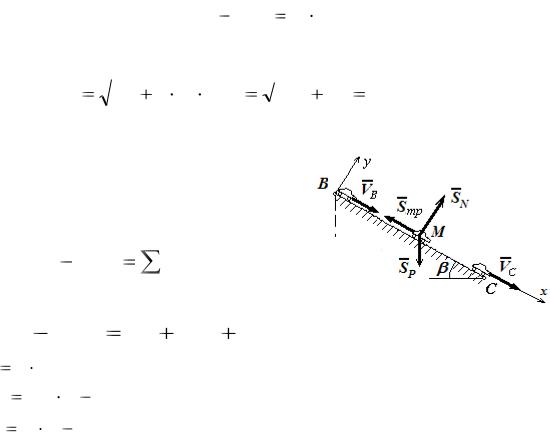
2. Определим скорость автомобиля в точке С (рисунок 24).
Так как задано время движения по участку ВС, целесообразно применить теорему об изменении количества движения точки
|
|
|
|
|
|
|
|
|
|
|
mVC |
mVB |
|
Sk . |
|
|
|
||
Или применительно к данной задаче |
|
|
|||||||
|
|
|
|
|
|
|
Рисунок 24 – Движение по участку ВС |
||
mVС |
mVВ |
SР |
Sтр |
SN , |
|||||
|
|
||||||||
|
|
|
|
|
|
|
|
||
где SP |
P t2 - импульс постоянной силы тяжести P , |
|
|||||||
|
|
|
|
|
|
|
|
||
Sтр |
Fтр t2 |
импульс постоянной силы Fтр , |
|
||||||
|
|
|
|
|
|
|
|
|
|
SN |
N |
t2 |
импульс постоянной силы N . |
|
|||||
В проекции на ось х получим |
|
|
|
||||||
|
|
|
|
mVСx – m VВx = SPx + Sтрx + SNx. |
(*) |
||||
Для постоянных сил вычислим проекции импульсов на ось х, |
|||||||||
|
|
SPx |
= mg cos 820 · t2 , |
Smpx = – Fmp· t2 = – f · N · t2, |
SNx = 0. |
||||
Составляя уравнение равновесия сил в проекции на ось у найдем, что N = mg · cos 80 и тогда выражение (*) с учетом проекций импульсов запишется в виде
mVС = m VВ + mg cos 820 · t2 – f · mg · cos 80 · t2
Упростив, найдем
VС = VВ + g · t2 · (cos 820 – f · cos 80).
Подставив в это выражение числовые значения, получим
VС = 17, 46 + 9,8 · 5 · (0,14 – 0,05 · 0,99) = 21,89 м/с.
72

3. Определим скорость автомобиля в точке К моста (рисунок 25).
Применим теорему об изменении кинетической энергии точки в конечной форме на участке СК
m V2 |
|
m V2 |
|
|
К |
|
С |
Аk |
|
2 |
2 |
|||
|
||||
или применительно к данной задаче
m VК2 |
|
m VС2 |
АР АN , |
(**) |
Рисунок 25 – Движение по мосту |
2 |
2 |
|
|||
|
|
|
|||
где АР - работа силы тяжести на перемещении СК, АN – работа нормальной реакции на том же перемещении.
Вычислим работу сил. |
|
|
||
|
АР = – m |
g · h1 = – m g · ( R cos 150 – (R – h)), |
||
АN = 0, так как реакция N перпендикулярна к направлению перемещения. |
||||
Подставляя эти выражения в формулу (**) и поделив на m, найдем |
||||
|
|
|
|
|
VК |
|
VС2 |
2 g (Rcos150 (R h)) 18,86м/с. |
|
4. Найдем реакцию моста при нахождении автомобиля в точке К.
Основной закон динамики для точки, находящейся на мосту в положении К, имеет вид
|
|
|
maК |
P |
N. |
Или в проекции на нормаль n (рисунок 26) maKn P  cos150 N.
cos150 N.
Откуда, учитывая, что аКn = mVK2 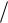 R , для нормальной реакции N получим
R , для нормальной реакции N получим
N = mg · cos 150 – m VK2 / R = 1000 ( 9,8 · 0,97 –18,862 /50) = 2392 Н = 2,39 кH.
Сила давления автомобиля на мост на основании закона равенства
действия и противодействия будет равна по модулю реакции N и направлена в противоположную сторону.
Таким образом, в точке К отрыва автомобиля от моста не происходит.
73
|
Пример решения задачи Д2 |
||
Однородная круглая пластина |
радиуса |
||
R = a = 2м и массы m1 = 40кг вращается вокруг |
|||
оси Oz с угловой скоростью ω0 = 10 с -1. С |
|||
пластиной жестко связан точечный груз А массы |
|||
m2 = 8кг (рисунок 26). В момент времени |
t0 = 0 |
||
на пластину начинает действовать пара сил с |
|||
постоянным моментом |
М = – 120 нм. |
|
|
Определить угловую скорость пластины в |
|||
момент времени Т = 2с. |
|
|
|
Решение. |
|
|
|
1. Рассмотрим |
механическую |
систему, |
|
состоящую из пластины и точечного груза. |
Рисунок 26 – Схема механизма |
||
Для решения |
задачи воспользуемся |
||
теоремой об изменении кинетического момента |
|||
относительно оси вращения Oz |
|
|
|
|
|
|
|
dKz |
|
|
e |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
mz (Fk ) |
|
(1) |
|
|
|
|
|||
|
|
|
|
dt |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
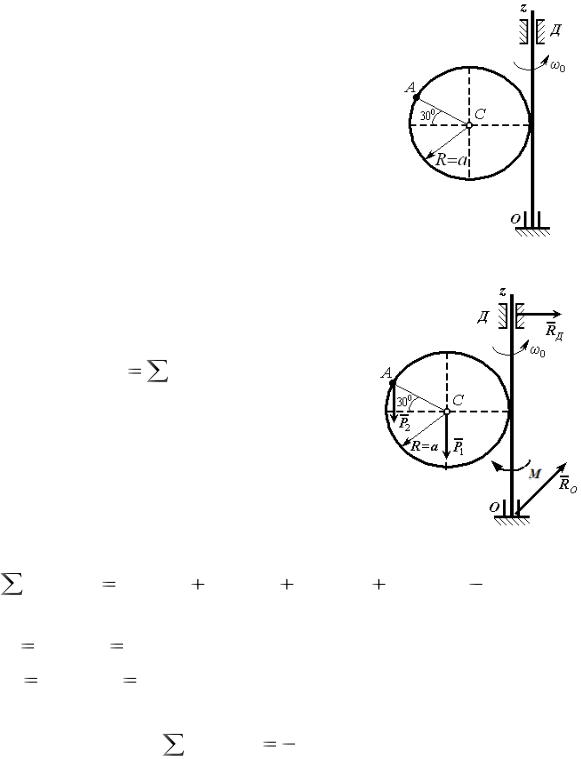
2. Вычислим сумму моментов внешних |
|
|
|
|
|||||||||||||
сил, действующих на систему. Приложим к |
|
|
|
|
|||||||||||||
системе |
внешние |
силы |
(рисунок |
27): |
силу |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
тяжести пластины |
Р1 |
, силу тяжести груза Р2 |
, |
|
|
|
|
||||||||||
вращающий |
момент |
М, а |
также |
реакции |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
подпятника |
R0 |
и подшипника |
RД . |
|
|
|
Рисунок 27 – Внешние силы системы |
||||||||||
Тогда |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
m (F e ) |
m (Р ) |
m (P ) |
m (R ) |
m (R |
Д |
) М. |
(2) |
|||||||||
|
z |
k |
|
|
z |
1 |
z |
2 |
|
z |
o |
z |
|
|
|||
Вычислим моменты внешних сил, входящие в выражение (2) |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
mz (Р1 ) |
mz |
(P2 ) |
|
|
0, |
так как силы |
Р1 |
и Р2 параллельны оси Оz; |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
mz (Ro ) mz (RД ) |
0, так как силы |
R0 и |
RД пересекают ось Оz. |
|
|||||||||||||
Следовательно, вместо выражения (2) имеем |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m (F e ) |
|
М. |
|
|
|
|
(3) |
||
|
|
|
|
|
|
|
|
|
z |
k |
|
|
|
|
|
|
|
Вычислим кинетический момент системы |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
КZ = КZпласт + КZгруз. |
|
|
|
(4) |
||||
Пластина совершает вращательное движение, поэтому |
|
|
|
||||||||||||||
КZпласт = JZ · ω
Осевой момент инерции пластины найдем по теореме Гюйгенса
JZ = JZС + m1 · d2 = m1 · R2 / 4 + m1 · R2 = 5 m1· R2 / 4,
74
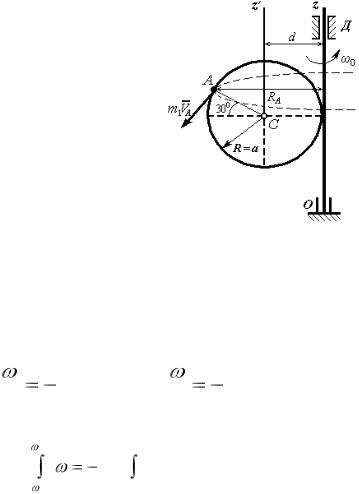
– определенный по данным справочной таблицы 4 момент инерции пластины относительно оси Сz, проходящей параллельно оси Оz и отстающей от нее на расстоянии d = R (рисунок 28).
Таким образом
КZпласт = JZ · ω = 1,25 m1· R2 · ω |
(5) |
|
Осевой момент инерции |
груза А |
|
относительно оси Оz равен моменту количества
движения m1VA (рисунок 28), то есть
КZгруз = M Z (m1VA ) = m1VA· RA
или, учитывая, что
VA = ω · RA и RA = (R +R cos 300),
получим
КZгруз = m1 ω · RA2 = m1 R2 (1+cos 300)2 · ω (6)
Рисунок 28 – Определение
Подставляя выражения (5) и (6) в формулу кинетического момента системы
(4), найдем кинетический момент системы
КZ = КZпласт + КZгруз = (1,25 + (1+cos 300)2) m1 R2 ω = 758,31 ω. |
(7) |
||||||
Подставляя выражения (7) и (3) в уравнение (1), имеем |
|
||||||
758,31 |
d |
|
120 или |
|
d |
0,16 |
|
dt |
|
dt |
|
||||
|
|
|
|
|
|||
Решая это дифференциальное уравнение, найдем |
|
|
|||||
|
|
T |
Т |
|
|
|
|
|
|
d |
0,16 |
dt |
|
|
|
0 |
0 |
|
|
|
|
||
|
|
|
|
|
|||
или
ωТ – ω0 = – 0,16 · Т.
Откуда получим
ωТ = ω0 – 0,16 · Т = 10 – 0,16 · 2 = 9,68 с –1.
Ответ ωТ = 9,68 с –1.
75

|
|
Пример решения задачи Д3 |
||
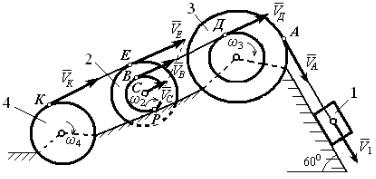
Механическая |
система |
|
||
(рисунок 29) состоит из груза 1, |
|
|||
ступенчатых шкивов 2 и 3 с |
|
|||
радиусами |
ступеней |
соответст- |
|
|
венно R2 = 3r2= 0,6 м, R3 = 2r3 |
|
|||
= 0, 4 м, блока 4 радиуса R4 = |
|
|||
0,8 м. Массы тел |
m1 = 15 кг, |
|
||
m2 = 8 кг, m3 = 6 кг, m4 = 1 кг. |
|
|||
Радиус инерции второго шкива |
|
|||
ρ2 = 0,5 R2. Масса шкива |
3 |
Рисунок 29 – Механическая система |
||
равномерно |
распределена |
по |
|
|
ободу радиуса R3. Тело 4 – сплошной однородный цилиндр. Коэффициент трения груза 1 о плоскость f = 0,1. Тела системы соединены друг с другом нитями параллельными соответствующим плоскостям. Под действием постоянной силы F = 20 Н система приходит в движение из состояния покоя. При движении на шкив 3 действует постоянный момент сопротивления М= 10 Н·м.
Определить угловую скорость блока 4 ω4 в тот момент времени, когда перемещение тела 1 станет равным s1 = 2 м. Все катки (шкивы), катятся по плоскостям без скольжения.
Решение
1.Рассмотрим движение неизменяемой механической системы, состоящей из тел 1, 2, 3, 4 соединенных нитями (рисунок 29).
2.Для определения ω4 воспользуемся теоремой об изменении кинетической энергии для неизменяемой системы
e |
|
Т – Т0 = ∑ Ak |
(1) |
3.Вычислим кинетическую энергию системы Т0 в начале движения. Так как в начальный момент система находилась в покое, то Т0 = 0.
4.Вычислим кинетическую энергию системы Т в конечном положении системы (когда тело 1 – переместилось на расстояние s = s1).
Величина Т будет равна сумме кинетических энергий всех тел, входящих в систему
Т = Т1 + Т2 + Т 3+ Т4 . |
(2) |
Учитывая, что тело 1 движется поступательно, тело 2 совершает плоское движение, а тела 3, 4 – совершают вращательное движение, найдем
Т1 = 12 m1V12; Т2 = 12 m2VC2 + 12 JC ω22; Т3 = 12 JC3 ω32; Т4 = 12 JC4 ω42. (3)
76
6. Выразим все входящие в формулы (3) скорости через |
искомую |
||||||
угловую скорость ω4. |
|
|
|
|
|
|
|
Блок 4 совершает вращательное движение, поэтому (рисунок 30) |
|
||||||
VК = ω4 R4 = 0,8 ω4. |
|
|
(4) |
|
|
||
Нить |
КЕ |
совершает |
|
|
|||
поступательное |
|
движение, |
|
|
|||
следовательно |
|
|
|
|
|
|
|
VЕ = VК = 0,8 ω4. |
|
|
|
(5) |
|
|
|
Шкив 2 совершает |
плоское |
|
|
||||
движение. М.ц.с. шкива в точке Р, |
Рисунок 30 – Скорости точек система |
||||||
поэтому |
|
|
|
|
|
|
|
|
|
ω2 = VЕ / (R2 + r2) = ω4. |
(6) |
||||
Скорость центра масс С шкива 2 |
|
|
|||||
|
|
|
|
|
VС = r2 ω2 = 0,2 ω4. |
(7) |
|
Скорость точки В шкива 2 |
|
|
|||||
|
|
|
VВ = 2 r2 ω2 = 0,4 ω4. |
(8) |
|||
Нить ДВ совершает поступательное движение, следовательно |
|
||||||
|
|
VВ = VД или |
0,4 ω4 = ω3 r3 |
|
|||
Откуда |
|
|
|
|
|
|
|
|
|
|
|
|
ω3 = 2 ω4 . |
(9) |
|
Шкив 3 находится во вращательном движении, следовательно |
|
||||||
|
|
|
VА = ω3 R3 = 2 ω4 · 0,4 = 0,8 ω4 |
(10) |
|||
Нить, соединяющая тела 1 и 3 находится в поступательном движении |
|||||||
(рисунок 30), поэтому |
|
|
|
|
|
|
|
|
|
|
|
|
V1 = VA = 0,8 ω4. |
(11) |
|
7. Вычислим моменты инерции, входящие в выражения (3) |
|
||||||
Для шкива 2 задан радиус инерции ρ2 = 0,5 R2 , следовательно |
|
||||||
|
|
J |
= m |
2 |
ρ 2 = 8 · 0,09 = 0,72 кг м2. |
(12) |
|
|
|
C |
|
2 |
|
|
|
|
|
|
|
|
|
77 |
|
Масса шкива 3 равномерно распределена по его ободу, поэтому
|
|
|
|
|
|
JC3 = m3 R32 = 6 · 0,16 = 0,96 кг м2. |
|
|
|
(13) |
|||||||||
|
Блок 4 сплошной однородный цилиндр, для которого |
|
|
|
|||||||||||||||
|
|
|
|
|
JC4 = m4 R42 / 2 = 1 · 0,82 / 2 = 0,32 кг м2 . |
|
|
|
(14) |
||||||||||
|
Выразим кинетическую энергию Т через искомую величину ω4. |
|
|||||||||||||||||
|
Подставив выражения (6) – (11), (12) – (14) в равенство (3) и далее в |
||||||||||||||||||
формулу (2), окончательно получим |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
Т = (4,8 + 0,16 + 0,36 + 1,92 + 0,16) ω42 = 7,4 ω42. |
(15) |
||||||||||||||
|
9. Найдем сумму работ всех действующих внешних сил при том |
||||||||||||||||||
перемещении, которое будет иметь система, когда тело 1 пройдет путь s1. |
|
||||||||||||||||||
|
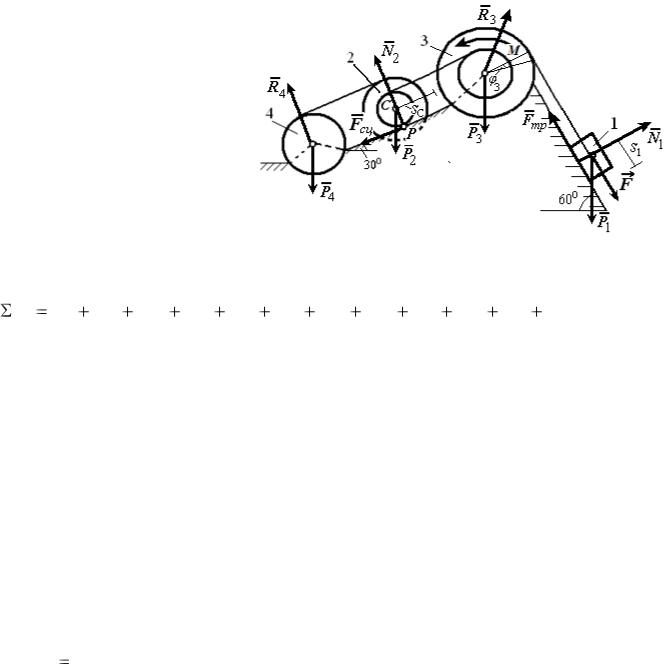
Изобразим |
действующие |
|
|
|
|
|
|
|
|
|||||||||
на |
систему |
внешние |
|
силы |
|
|
|
|
|
|
|
|
|||||||
(рисунок 31): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
активные |
F , |
P 1, |
|
P 2, |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P 3, P 4; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
реакции |
связей |
N |
1, |
|
N 2, |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
R 3, R 4; |
Fmp , Fcц , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
момент сопротивления М. |
|
|
|
|
|
|
|
|
||||||||||
|
Тогда |
сумма |
|
|
работ |
|
Рисунок 31 |
– Внешние силы и перемещения |
|||||||||||
внешних сил, действующих на |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||
систему, будет |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Аke |
|
|
АF |
АР |
Атр |
|
АР |
АР |
АР |
AN |
AN |
AR |
AR |
Acц АМ . |
(16) |
|||
|
|
|
|
|
1 |
|
|
|
|
2 |
3 |
4 |
1 |
2 |
3 |
4 |
|
||
|
Обозначим: sС – перемещение центра шкива 2 (рисунок 31); φ3 – угол |
||||||||||||||||||
поворота шкива 3 и вычислим работы всех сил входящих в выражение (16). |
|
||||||||||||||||||
|
АF = F · s1 – так как сила F постоянная и совпадает с направлением |
||||||||||||||||||
перемещения; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
А |
|
= Р1 |
· h1 = m1 g · s |
1 |
· cos 300, где h1 – вертикальное смещение груза 1; |
|||||||||||||
|
|
Р |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
АР |
=–Р2 · hС = –m2 g · sС · sin 300, где hС - вертикальное смещение точки С; |
|||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Атр = – Fтр s1 = –f N1 s1= –fm1g s1 · cos 600; |
|
|
|
|
|
|||||||||||||
|
АР3 |
= АР4 |
= 0, так как эти силы приложены к неподвижным точкам; |
|
|||||||||||||||
|
АN1 |
= 0, так как эта сила перпендикулярна к направлению перемещения; |
|||||||||||||||||
|
АN 2 = 0, так как эта сила приложена к неподвижной точке (м.ц.с.); |
|
|||||||||||||||||
|
Aсц |
0, так как эта сила приложена к неподвижной точке (м.ц.с.); |
|
||||||||||||||||
|
АR3 |
= АR4 |
= 0, так как эти силы приложены к неподвижным точкам; |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
78 |
|
|
|
|
|
|
|

АM = – М · φ3 – работа момента сопротивления. Таким образом, вместо выражения (16), получим
Аke = F · s1 + m1 g · s1 · cos300 – f m1 g s1 · cos600 – m2 g · sС · sin300 – М · φ3. (17)
Выразим перемещения sС и φ3 через перемещение s1 используя идентичность зависимостей между скоростями и соответствующими перемещениями.
Определяя ω4 из выражений (7) и (11), найдем
ω4 = 5 VС и ω4 = 1,25 V1.
Откуда
VC = 0,25 V1.
Правило. Если зависимость между скоростями точек системы сохраняется во все время движения, то зависимость между перемещениями этих точек идентична.
Применяя это правило установим связь скоростями точки С и тела 1 |
|
sC = 0,25 s1. |
(18) |
Определяя ω3 из выражений (10) и (11), найдем |
|
V1 = ω3 R3 или ω3 = V1/ R3 |
|
Откуда |
|
ω3 = 2,5 V1. |
|
Согласно приведенному выше правилу зависимость углового |
|
перемещения φ3 от линейного перемещения s1 |
определится выражением |
φ3 = 2,5 s1. |
(19) |
Подставляя соотношения (18) и (19) в выражение (17), найдем |
|
Аke = F ·s1 + m1 g · s1 · cos300 –f m1 g s1 · cos 600–m2 g · 0,25s1 ·sin 300 – М ·2,5s1 =
= 20 ·2 + 2 · 9,8 · (15 · 0,86 – 0,1 · 15 · 0,5 – 8 · 0,25 · 0,5) – 10· 2,5 · 2 = |
(20) |
= 40+19,6 · (12,9 – 0,75 –1) – 50 = 208,54 Дж.
Подставляя выражения (15) и (20) в уравнение (1), получим
7,4 ω42 = 208,54
Откуда найдем
ω4 = 5,31 с -1.
Ответ: угловая скорость ω4 = 5,58 с -1.
79

Пример решения задачи Д4
Вертикальный вал АВ (рисунок 32), вращающийся с постоянной угловой скоростью ω, закреплен подпятником в точке А и цилиндрическим подшипником в точке В. К валу в точке К жестко прикреплен невесомый стержень КD длиной l1 с
точечной массой |
m1 |
на конце и |
однородный |
||||||
стержень ЕL, массой m2 |
и длиной l2; |
оба стержня |
|||||||
лежат в одной плоскости. |
|
|
|
|
|
|
|||
Дано: b1 = 0,6 м, b2 = 0,2 м, b3 = 0,2 м, α = 300, |
|||||||||
β = 600, l = 0,5 м, |
l |
2 |
= 0,8 м, m |
1 |
= 2 кг, m |
2 |
= 4 кг, |
||
1 |
|
|
|
|
|
|
|||
ω = 4 с –1. |
|
|
|
|
|
|
|
|
Рисунок 32 – Вращение вала |
Определить: реакции подпятника А и подшипника В.
Решение
1.Для решения задачи воспользуемся принципом Даламбера. Рассмотрим механическую систему, состоящую из вала АВ, стержня EL и груза D (рисунок
32).
2.Изобразим действующие на систему внешние силы: силы тяжести P1 , P2 , составляющие Х А , Y А реакции подпятника
иреакцию Х В подшипника (рисунок 33).
3.Вычислим силы инерции.
Массу имеют два тела: груз D и однородный стержень EL.
3.1 Вычислим силу инерции груза D.
Так как вращение системы равномерное, то
точка D имеет только нормальное ускорение |
n |
|
|
|
|
|
|||||||
а |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
D |
|
|
|
|
|
(рисунок 33). Тогда сила инерции груза D |
|
|
|
|
Рисунок 33 – Система сил, |
||||||||
и |
|
|
|
|
n |
|
|
|
|
|
|||
m1 |
m1 |
|
|
|
|
|
|
приложенная к валу |
|||||
F1 |
аD |
аD . |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
То есть она будет направлена в сторону противоположную ускорению aD , |
|||||||||||||
и численно равна |
|
|
|
|
|
|
|
|
|
|
|
|
|
F1u = m1 · anD |
|
|
|
||||||||||
= m1 · ω2 l1 sin β = 2 · 42 · 0,5 · 3 /2 = 8 · 1,73 = 13,86 Н. |
|||||||||||||
3.2 Вычислим силы инерции стержня EL. |
|
|
|
|
|
|
|||||||
Так как вал вращается равномерно |
(ω = const), |
то элементы стержня |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
имеют только нормальные ускорения |
аnk |
(рисунок 33), |
направленные к оси |
||||||||||
вращения и численно равные а |
|
= ω2 |
h , где |
h |
|
– расстояние элемента от оси |
|||||||
|
|
|
|
nk |
|
k |
|
|
k |
|
|
|
|
(рисунок 33). Тогда силы инерции F |
и , будут направлены от оси вращения и |
||||||||||||
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
80 |
|
|
|
|
|
|
|
